Linear regression 은 어떤 input에 대한 실수값의 output을 예측하는 문제이다.
1. Univariate Linear Regression
1.1 The Hypothesis Function
h ( x ) = θ 0 + θ 1 x h(x) = \theta_0 + \theta_1 x h ( x ) = θ 0 + θ 1 x Hypothesis란, input (feature)과 output (target)의 관계를 나타내는 함수이다. h \,h h
한가지 feature를 이용한 Linear Regression을 "Univariate Linear Regression" 이라고 부른다.
1.2 Cost function
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1) = \frac{1}{2m} \displaystyle\sum_{i=1}^{m}{(\hat{y}^{(i)}-y^{(i)})^2} = \frac{1}{2m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})^2} J ( θ 0 , θ 1 ) = 2 m 1 i = 1 ∑ m ( y ^ ( i ) − y ( i ) ) 2 = 2 m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) 2 e r r o r = h ( x ( i ) ) − y ( i ) error = h(x^{(i)})-y^{(i)} e r r o r = h ( x ( i ) ) − y ( i )
m : m :\, m : x i : x^{i} :\, x i : y i : y^{i} :\, y i : θ 0 : \theta_0 : θ 0 : θ 1 : \theta_1 : θ 1 :
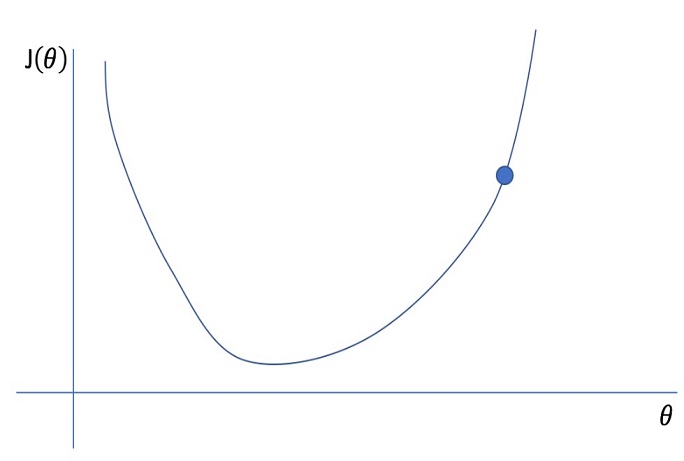
Hypothesis Function의 정확도를 측정하기 위해 Cost Function을 이용한다.
Training Dataset을 학습해 Parameter θ 0 , θ 1 \,\theta_0, \theta_1 θ 0 , θ 1
error값은 양수값일 수도 있고 음수값일 수도 있기 때문에 이들의 제곱값의 합을 구하여 그 합이 최소가 되는 Parameter를 찾는 방법 이 일반적이다.mean-squared-error (MSE) 이다.
다만, 평균이라면 Data의 개수인 m m m 2 m 2m 2 m
θ 0 = 0 \theta_0 = 0 θ 0 = 0 θ 0 ≠ 0 \theta_0 \ne 0 θ 0 = 0
2. Parameter Learning - Gradient Descent
2.1 Gradient Descent Algorithm
Gradient descent는 Cost function을 최소화하기 위해 이용할 수 있는 방법 중 하나이며, Cost function 말고도 각종 Optimization에 이용되는 일반적인 방법이다.
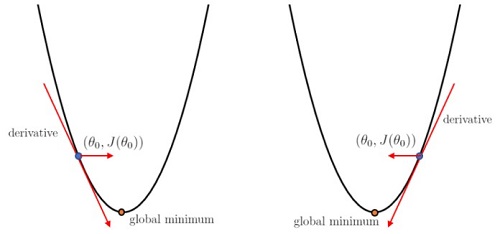
a r g m i n θ 0 , θ 1 J ( θ 0 , θ 1 ) argmin_{\theta_0, \theta_1}J(\theta_0, \theta_1) a r g m i n θ 0 , θ 1 J ( θ 0 , θ 1 ) θ 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) \theta_0 := \theta_0 - \alpha{\partial \over \partial\theta_0}J(\theta_0, \theta_1) θ 0 : = θ 0 − α ∂ θ 0 ∂ J ( θ 0 , θ 1 ) θ 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) \theta_1 := \theta_1 - \alpha{\partial \over \partial\theta_1}J(\theta_0, \theta_1) θ 1 : = θ 1 − α ∂ θ 1 ∂ J ( θ 0 , θ 1 ) ∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j [ 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 ] = 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) {\partial \over \partial\theta_j}J(\theta_0, \theta_1) = {\partial \over \partial\theta_j}[\frac{1}{2m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})^2}] = \frac{1}{m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})}\cdot x^{(i)} ∂ θ j ∂ J ( θ 0 , θ 1 ) = ∂ θ j ∂ [ 2 m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) 2 ] = m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) 주의해야할 점은 Parameter들을 한번에 업데이트해야한다는 점이다.θ 0 \theta_0 θ 0 θ 1 \theta_1 θ 1
편미분항 ∂ ∂ θ j J ( θ 0 , θ 1 ) {\partial \over \partial\theta_j}J(\theta_0, \theta_1) ∂ θ j ∂ J ( θ 0 , θ 1 )
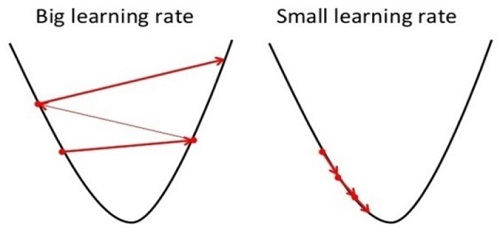
2.2 Learning Rate α > 0 \alpha > 0 α > 0
Learning Rate가 너무 작으면 수렴하는데에 오래걸리는 문제가 생기고, 너무 크면 최소값에 이르지 못해 수렴하지 못하거나 심지어 발산하는 문제가 발생할 수 있다. 그러므로 적절한 learning rate을 고르는 것이 중요하다.
대부분의 경우, 최적값에 수렴할수록 편미분항의 크기가 작아져서 조금씩 업데이트되기 때문에 α \alpha α
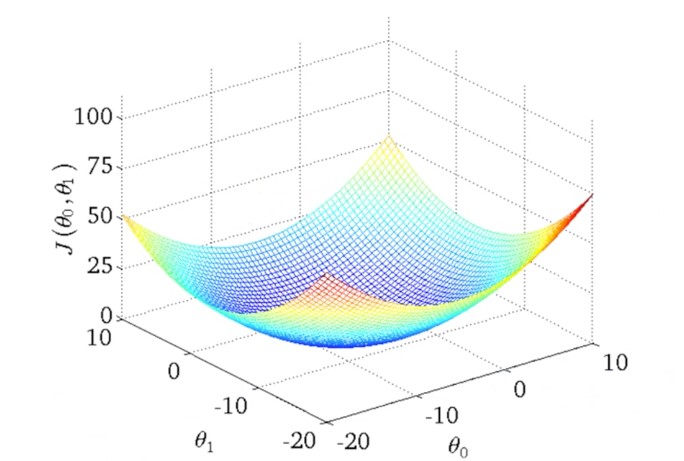
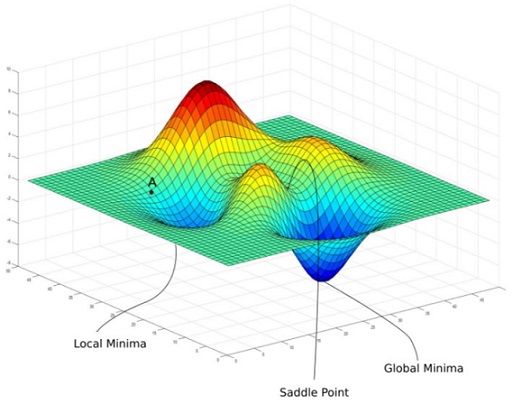
2.3 Global Minimum v.s Local Minimum
Gradient Descent가 수렴할 수 있는 여러 개의 Local Minimum이 있을 수 있다.
3. Multivariate Linear Regression
3.1 Cost Function
h ( x ( i ) ) = θ 0 + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + θ 3 x 3 ( i ) + ⋅ ⋅ ⋅ + θ n x n ( i ) h(x^{(i)}) = \theta_0 + \theta_1x_1^{(i)} + \theta_2x_2^{(i)} + \theta_3x_3^{(i)} + \cdot\cdot\cdot + \theta_nx_n^{(i)} h ( x ( i ) ) = θ 0 + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + θ 3 x 3 ( i ) + ⋅ ⋅ ⋅ + θ n x n ( i ) X = [ x 1 , 1 x 1 , 2 ⋯ x 1 , n x 2 , 1 x 2 , 2 ⋯ x 2 , n ⋮ ⋮ ⋱ ⋮ x m , 1 x m , 2 ⋯ x m , n ] Θ = [ θ 0 θ 1 ⋮ θ n ] X = \left[\begin{array}{rrr} x_{1,1} & x_{1,2} & \cdots & x_{1,n} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m,1} & x_{m,2} & \cdots & x_{m,n} \end{array}\right] \quad\quad\quad \Theta = \left[\begin{array}{rrr} \theta_0 \\ \theta_1 \\ \vdots\\ \theta_n \end{array}\right] X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 , 1 x 2 , 1 ⋮ x m , 1 x 1 , 2 x 2 , 2 ⋮ x m , 2 ⋯ ⋯ ⋱ ⋯ x 1 , n x 2 , n ⋮ x m , n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ Θ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ θ 0 θ 1 ⋮ θ n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ h ( X ) = X Θ h(X) = X\Theta h ( X ) = X Θ J ( θ ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})^2} J ( θ ) = 2 m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) 2 V e c t o r i z e ⇒ J ( Θ ) = 1 2 m ( X Θ − Y ) T ( X Θ − Y ) Vectorize\;\;\; \Rightarrow \;\;\;J(\Theta) = {1 \over 2m}(X\Theta-Y)^T(X\Theta-Y) V e c t o r i z e ⇒ J ( Θ ) = 2 m 1 ( X Θ − Y ) T ( X Θ − Y )
n : n \;\,: n : x n i : x_n^i : x n i : n n n i t h i^{th} i t h x x x n n n
3.2 Gradient Descent for Multiple Variables
Gradient descent는 변수가 하나일 때와 기본적으로 같은 꼴이지만 n n n
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , ⋅ ⋅ ⋅ , θ n ) = θ j − α 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) \theta_j := \theta_j - \alpha{\partial \over \partial\theta_j}J(\theta_0, \cdot \cdot \cdot , \theta_n) = \theta_j - \alpha\frac{1}{m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})}\cdot x_j^{(i)} θ j : = θ j − α ∂ θ j ∂ J ( θ 0 , ⋅ ⋅ ⋅ , θ n ) = θ j − α m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) 이를 각 Parameter별로 풀어쓰면,
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) ⋮ θ n : = θ n − α 1 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) ⋅ x n ( i ) \theta_0 := \theta_0 - \alpha\frac{1}{m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})}\cdot x_0^{(i)} \\ \theta_1 := \theta_1 - \alpha\frac{1}{m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})}\cdot x_1^{(i)} \\ \vdots \\ \theta_n := \theta_n - \alpha\frac{1}{m} \displaystyle\sum_{i=1}^{m}{(h(x^{(i)})-y^{(i)})}\cdot x_n^{(i)} θ 0 : = θ 0 − α m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) θ 1 : = θ 1 − α m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) ⋮ θ n : = θ n − α m 1 i = 1 ∑ m ( h ( x ( i ) ) − y ( i ) ) ⋅ x n ( i ) ∇ J ( Θ ) = [ ∂ J ( θ ⃗ ) ∂ θ 0 ∂ J ( θ ⃗ ) ∂ θ 1 ⋮ ∂ J ( θ ⃗ ) ∂ θ n ] ∇ J ( Θ ) = 1 m X T ( X Θ − Y ) \nabla J(\Theta) = \left[\begin{array}{rrr} {\partial J(\vec{\theta}) \over \partial\theta_0} \\ \\ {\partial J(\vec{\theta}) \over \partial\theta_1} \\\\ \vdots\\ \\ {\partial J(\vec{\theta}) \over \partial\theta_n} \end{array}\right] \quad\quad \nabla J(\Theta) = \frac{1}{m}X^T(X\Theta - Y) ∇ J ( Θ ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ θ 0 ∂ J ( θ ) ∂ θ 1 ∂ J ( θ ) ⋮ ∂ θ n ∂ J ( θ ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∇ J ( Θ ) = m 1 X T ( X Θ − Y ) Θ : = Θ − α ∇ J ( Θ ) \Theta := \Theta - \alpha\nabla J(\Theta) Θ : = Θ − α ∇ J ( Θ ) 4. Gradient Descent in Practice
4.1 Feature Scaling
Feature Scaling은 서로 다른 Scale or Unit을 가지는 Feature들을 동일한 범위로 조정하는 데이터 전처리 과정이다.
4.1.1 Normalization (Min-Max scaling)
x ′ = x − x m i n x m a x − x m i n x^{\prime} = \frac{x - x_{min}}{x_{max} - x_{min}} x ′ = x m a x − x m i n x − x m i n
x m a x x_{max} x m a x x m i n x_{min} x m i n
4.1.2 Standardization
x ′ = x − μ σ x^{\prime} = \frac{{x - \mu}}{{\sigma}} x ′ = σ x − μ
μ \mu μ σ \sigma σ
5. Polynomial Regression
Hypothesis Function이 반드시 Linear 하여야 하는 것은 아니다. 예를들면 2차함수나 3차함수 또는 제곱근 함수 등의 형태를 이용할 수 있다.
가령, h ( x ) = θ 0 + θ 1 x 1 h(x) = \theta_0 + \theta_1 x_1 h ( x ) = θ 0 + θ 1 x 1 x 1 x_1 x 1
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 x 2 = x 1 2 h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 \quad\quad x_2 = x_1^2 h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 x 2 = x 1 2 주의할 점은, 이렇게 feature를 만들면 feature scaling이 더욱 중요해진다는 점이다.x 1 x_1 x 1 x 2 x_2 x 2
6. Computing Parameters Analytically
6.1 Normal Equation
Model parameter θ \theta θ
N o r m a l E q u a t i o n : Θ ^ = ( X T X ) − 1 X T Y Normal \,Equation : \hat{\Theta} = (X^TX)^{-1}X^TY N o r m a l E q u a t i o n : Θ ^ = ( X T X ) − 1 X T Y