그래프 (Graph)
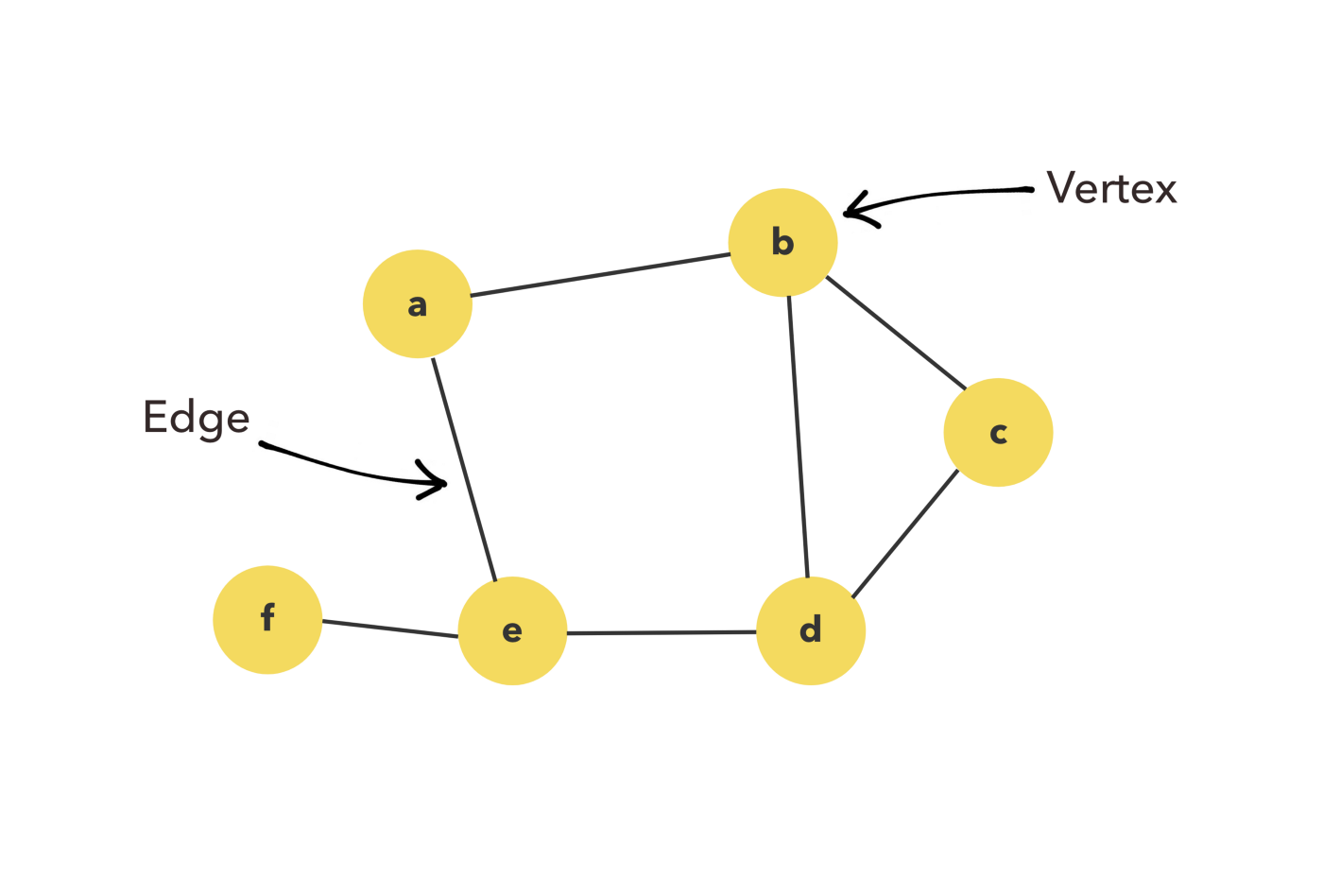
: 정점(vertex)과 정점 사이를 연결하는 간선(edge)으로 이루어진 비선형 자료구조
그래프는 정점 집합과 간선 집합으로 표현할 수 있다.
- 정점 : 노드(node)라고도 하며, 데이터가 저장되는 그래프의 기본 원소
- 간선 :정점 간의 관계를 나타내는 정점을 이어주는 선
그래프 용어
- 진입차수(in-degree) : 한 정점에 진입하는 간선이 몇 개인지 나타낸다.
- 진출차수(out-degree) : 한 정점에 진출하는 간선이 몇 개인지 나타낸다.
- 두 정점을 바로 이어주는 간선이 있다면, 이 두 정점은 인접하다(adjecent)고 한다.
- 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클(cycle)이 있다고 한다.
- 정점에서 진출하는 간선이 곧바로 자신에게 진입하는 경우, 자기 루프(selft loop)를 가졌다고 한다.
- 정점에 연결되어있는 간선이 없다면, 그 정점은 고립(isolated)되어있다고 한다.
그래프의 종류
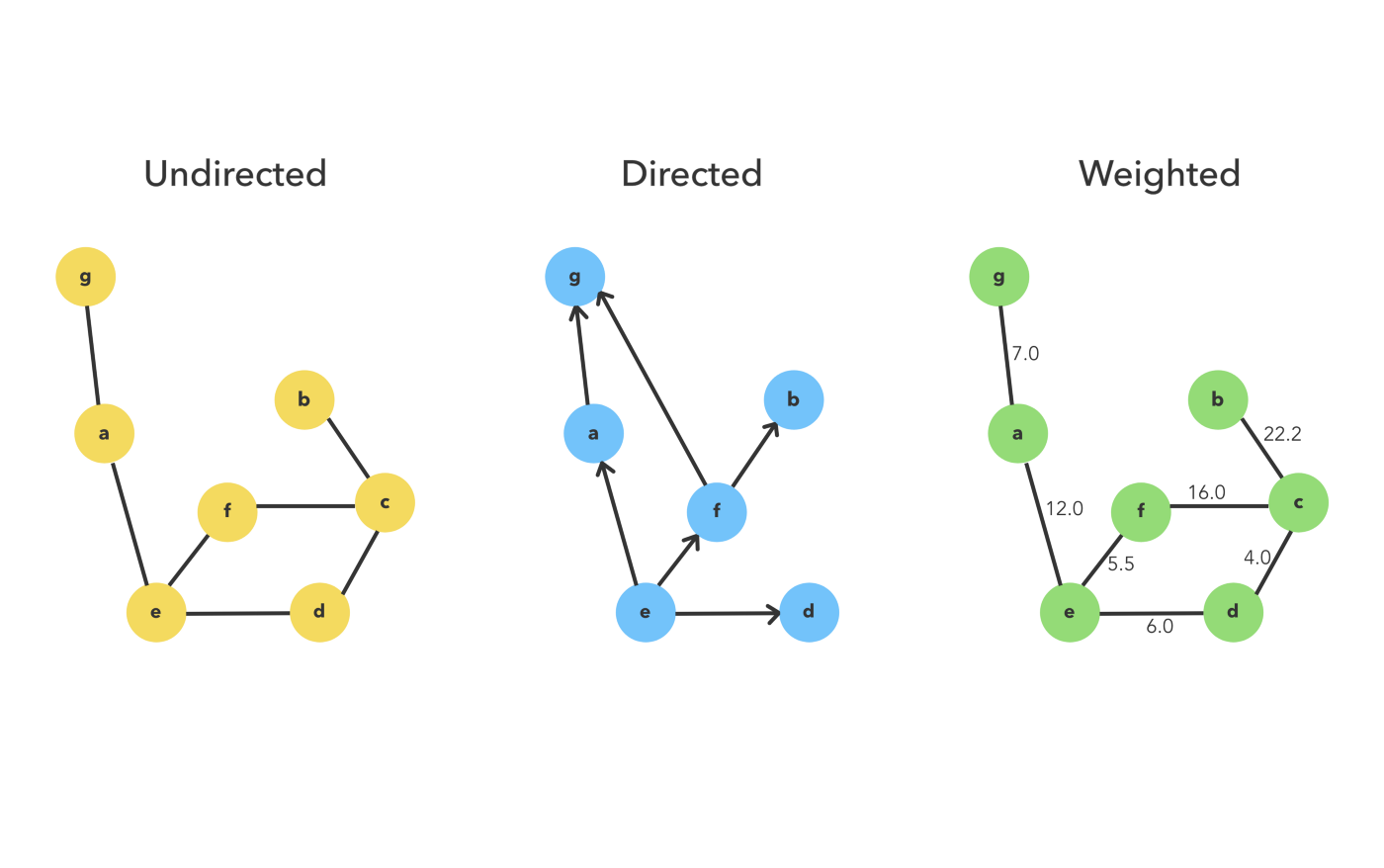
방향 그래프(Directed Graph)
: 간선에 방향이 있어, 시작하는 정점과 도착하는 정점이 있다.
무향 그래프(Undirected Graph)
: 간선에 방향이 없고, 두 정점이 양 방향으로 서로를 가리킨다.
가중치 그래프(Weighted Graph)
: 연결의 강도(추가적인 정보)가 얼마나 되는지 적혀져 있는 그래프
비가중치 그래프(Unweighted Graph)
: 연결의 강도가 적혀있지 않은 그래프
그래프의 표현 방식
인접 행렬
: 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원의 배열의 형태로 나타낸다.
- 두 정점 사이에 관계가 있는지 없는지 확인하기에 용이하다.
- 가장 빠른 경로를 찾고자 할 때 주로 사용된다.
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.
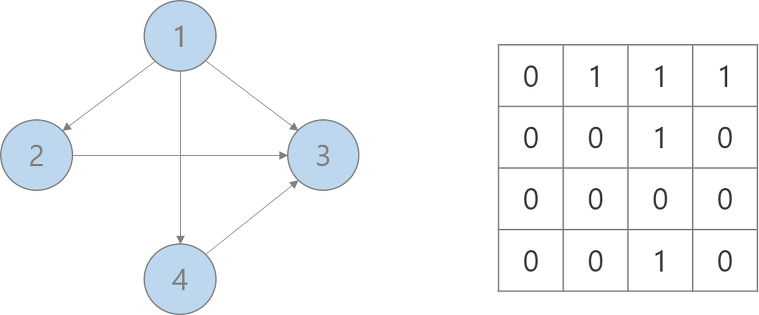
const graph = Array.from(Array(4), () => Array(4).fill(0));
// [0, 0, 0, 0]
// [0, 0, 0, 0]
// [0, 0, 0, 0]
// [0, 0, 0, 0]
graph[0][1] = 1; // 0 → 1
graph[0][2] = 1; // 0 → 2
graph[0][3] = 1; // 0 → 3
graph[1][2] = 1; // 1 → 2
graph[3][2] = 1; // 3 → 2- 간선에 가중치를 넣고 싶다면
null과 가중치값을 넣으면 된다. - 무방향 그래프를 구현한다면 모든 값을 대칭으로 넣어주면 된다.
Array.from의 사용Array.from(Array(5), () => 1); // 크기가 5인 빈 배열을 1로 채운다. // [1, 1, 1, 1, 1]
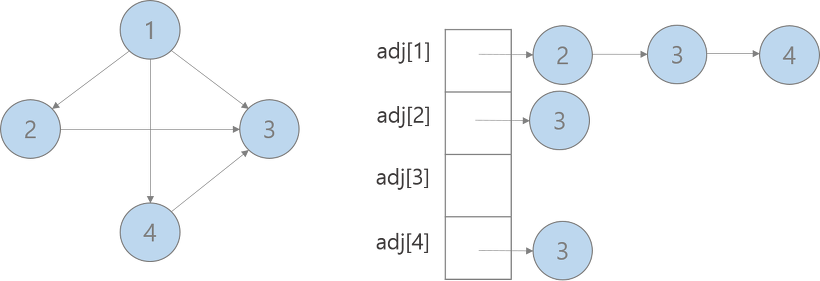
인접 리스트
: 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 나타낸다.
각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있다.
const graph = Array.from(Array(4), () => []);
// [ [], [], [], [] ]
graph[0].push(1);
graph[0].push(2);
graph[0].push(3);
graph[1].push(2);
graph[3].push(2);
// [
// [1, 2, 3]
// [2]
// []
// [2]
// []
// ]
JavaScript의 배열은 연결 리스트처럼 무한정 늘어날 수 있기 때문에, 정점의 수만큼 배열을 만들고, 연결할 정점을 배열에 추가하면 된다.
그래프의 사용
- 소셜 미디어의 네트워크를 나타낼 때 사용된다. 각 유저는 정점이고, 사용자가 연결되면 간선이 생성된다.
- 검색 엔진의 웹 페이지와 링크를 나타내는데 사용된다. 각 웹 페이지는 정점이고, 하이퍼링크에 의해 연결되면 간선이 생성된다.
➡️ 페이지 랭크(Page Rank)에 사용된다.
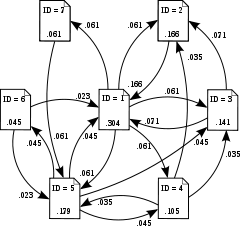
- GPS에서 위치와 경로를 나타낼 때 사용된다. 각 장소는 정점이고, 장소를 연결하는 경로가 간선이다.
➡️ 두 위치의 최단 경로를 계산하는 데에 사용된다.
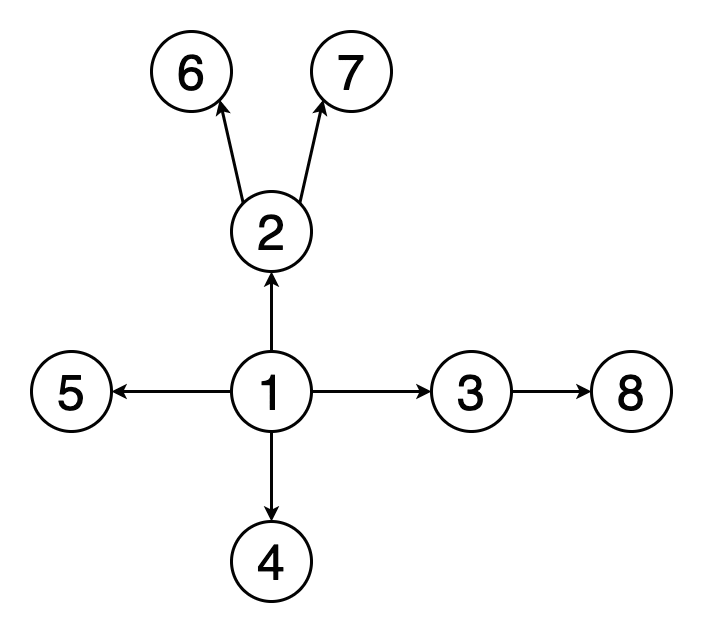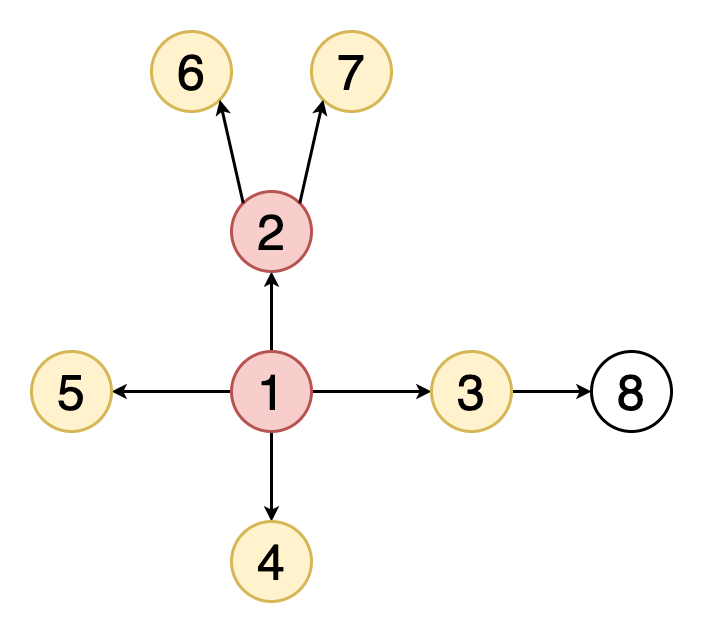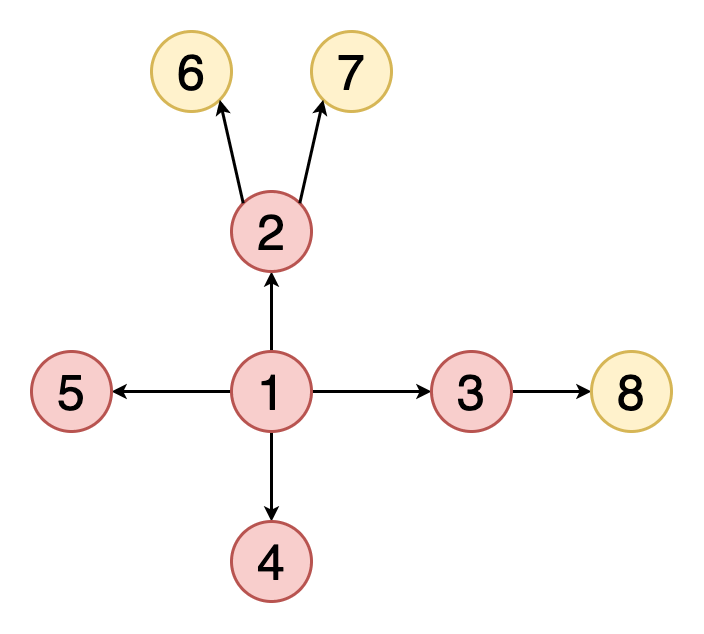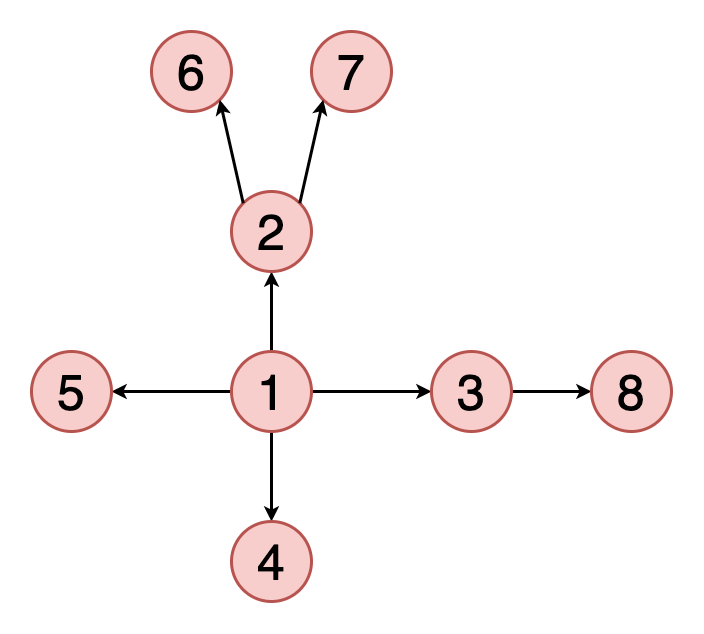
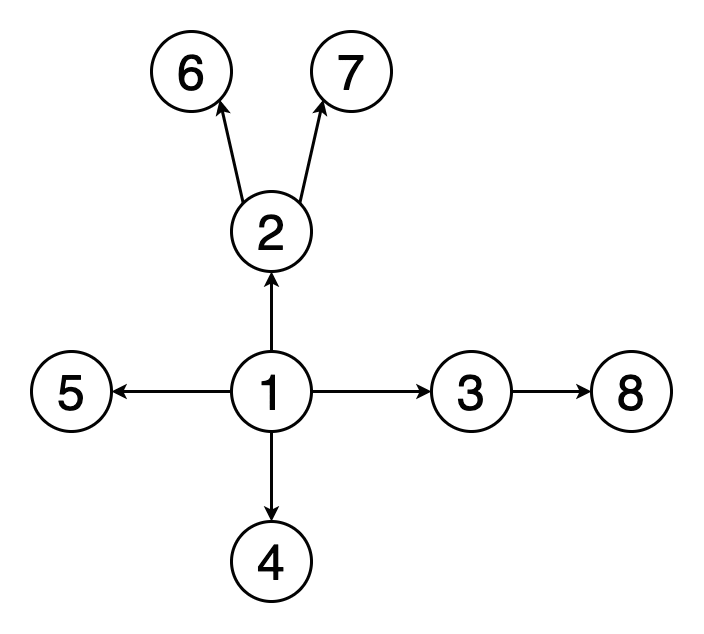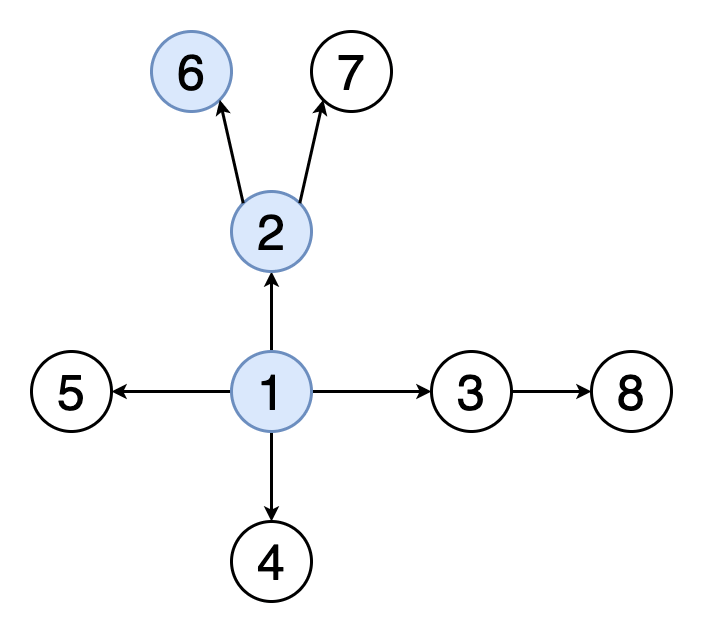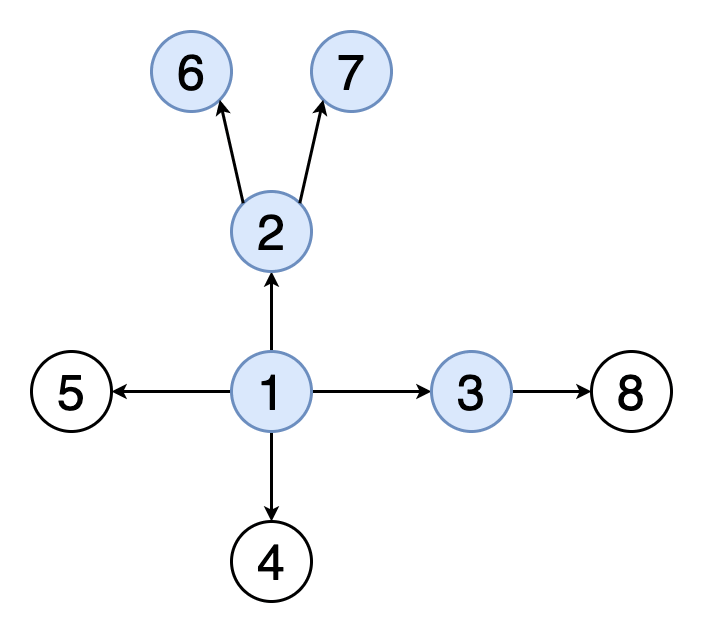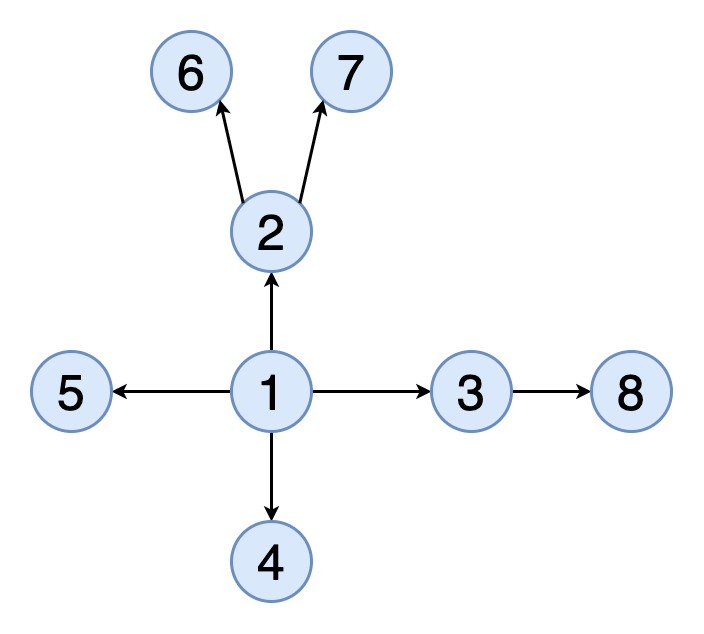
그래프의 탐색
그래프 탐색의 목적은 하나의 정점에서 시작하여 모든 정점에 한 번씩 방문하는 것이다.
그래프의 데이터는 배열처럼 정렬되어 있지 않으므로, 원하는 자료를 찾으려면 하나씩 모두 방문해서 찾아야 한다.
가장 대표적인 그래프 탐색 알고리즘으로는 BFS와 DFS가 있다.
BFS (Breadth-First Search)
: 너비를 우선적으로 탐색하는 방식 (너비 우선 탐색)
시작 정점에서 가까운 정점부터 탐색하며, 더 이상 탐색할 정점이 없다면 그 다음 떨어져 있는 정점을 순서대로 방문한다.
- 주로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
DFS (Depth-First Search)
: 깊이를 우선적으로 탐색하는 방식 (깊이 우선 탐색)
하나의 경로를 끝까지 탐색한 후, 찾는 값이 아니라면 다음 경로로 넘어가 탐색한다.
- 한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색할 때 사용한다.
- BFS보다 탐색 시간은 오래 걸리지만 모든 노드를 완전히 탐색할 수 있다.