트리(Tree)
: 정점을 가리키는 간선이 하나밖에 없는 구조를 가지고 있는 방향 그래프의 일종
트리의 특징
- 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가진다.
- 정점이
n개인 트리는 반드시n -1개의 간선을 가진다. - 루트에서 특정 정점으로 가는 경로는 유일하다.
이진 트리(Binary Tree)
: 각 정점이 최대 2개의 자식을 가지는 트리
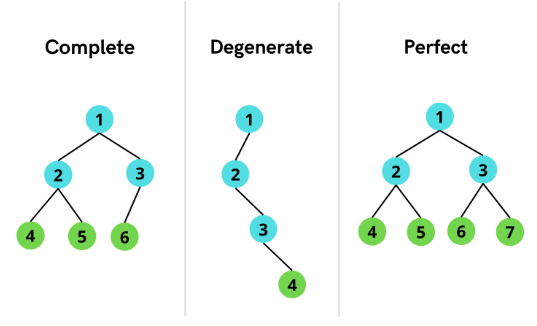
이진 트리의 종류
완전 이진 트리
: 마지막 레벨을 제외하고 모든 정점이 채워져 있는 트리
편향 트리
: 한 방향으로만 정점이 이어져 있는 트리
포화 이진 트리
: 마지막 레벨까지 모든 정점이 채워져 있는 트리
이진 트리의 특징
- 정점이
n개인 이진 트리는 최악의 경우 높이(height)가N이 될 수 있다.
(n개의 정점을 가진 편향 트리) - 정점이
n개인 포화 / 완전 이진 트리의 높이는log N이다.
(레벨이 증가됨에 따라 2개씩 정점이 증가하기 때문) - 높이가
h인 포화 이진 트리는2ʰ - 1개의 정점을 가진다.
(e.g. 높이가 3인 포화 이진트리의 정점 개수는 2³ - 1 = 7개) - 보통 이진 트리 자체를 사용하는 경우는 많지 않고, 다음 자료구조에 응용된다.
- 이진 탐색 트리
- 힙
- AVL 트리
- 레드 블랙 트리
이진 트리의 구현 방법
: 1차원 배열 혹은 요소에 링크가 2개 존재하는 연결 리스트로 구현할 수 있다.
배열
- 0번째 index는 편의상 비워둔다. (
undefined) - Left =
index * 2 - Right =
index * 2 + 1 - Parent =
floor(index / 2)
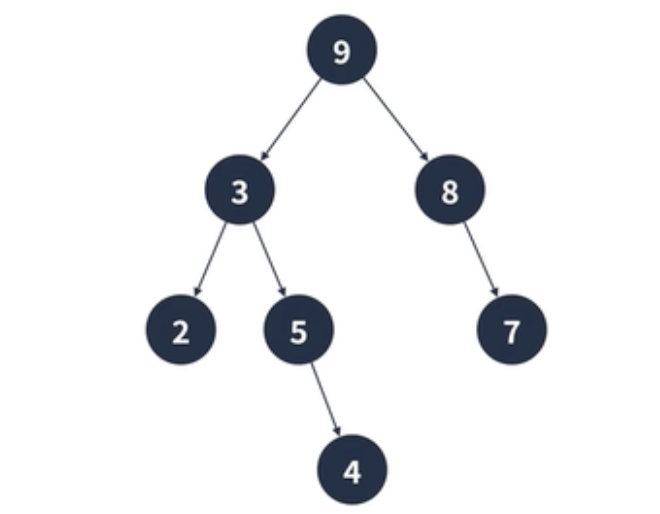
위의 트리를 배열로 나타내면 아래와 같다.
const tree = [undefined, 9, 3, 8, 2, 5, undefined, 7, undefined, undefined, undefined, 4];
const tree = [ u, // 0
9, // 1
3, 8, // 2 3
2, 5, u, 7, // 4 5 6 7
u, u, u, 4 ﹒ ﹒ ﹒ ﹒ // 8 9 10 11
];연결 리스트
위의 트리를 연결 리스트로 나타내면 아래처럼 표현할 수 있다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class Tree {
contructor(node) {
this.root = node;
}
display() {
// Level Order
const queue = new Queue();
queue.enqueue(this.root);
while (queue.size) {
const currentNode = queue.dequeue();
console.log(currentNode.value);
if (currentNode.left) queue.enqueue(currentNode.left);
if (currentNode.right) queue.enqueue(currentNode.right);
}
}
}
const tree = new Tree(new Node(9));
tree.root.left = new Node(3);
tree.root.right = new Node(8);
tree.root.left.left = new Node(2);
tree.root.left.right = new Node(5);
tree.root.right.right = new Node(7);
tree.root.left.right.right = new Node(4);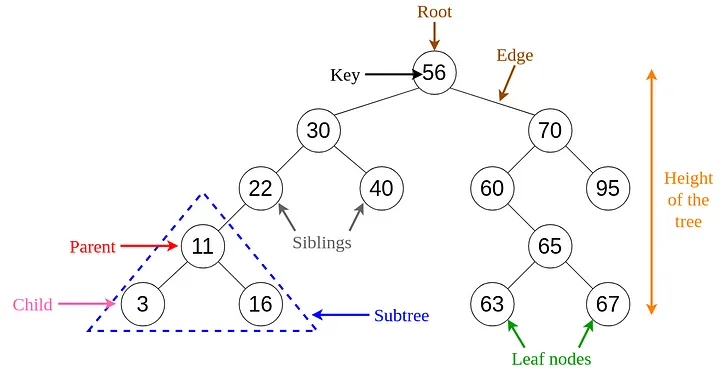






알고리즘 너무 어려워요 ㅠㅠ 트리 자료구조 배울때 힘들었는데 깔끔하게 정리해주셔서 좀더 이해가 갔습니다