동적 계획법 (Dynamic Programming)

지은·2023년 5월 25일

Algorithm

목록 보기

26/33

다이나믹 프로그래밍

: 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법

이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다.
즉, 한 번 해결한 문제는 다시 해결하지 않는다. (효율성 ↑)
완전 탐색을 이용했을 때 매우 비효율적인 시간 복잡도를 가지는 문제라고 하더라도, 다이나믹 프로그래밍을 사용하면 시간복잡도를 획기적으로 줄일 수 있다.

완전 탐색 (Exhaustive search, Brute force)

: 모든 경우의 수를 시도하는 방법

상대적으로 구현이 간단하고, 해가 존재하면 항상 찾게 된다.

경우의 수에 따라 실행 시간이 비례하기 때문에, 입력값의 범위가 작은 경우 유용하다.
참고 - [알고리즘] 완전탐색

다이나믹 프로그래밍의 조건

다이나믹 프로그래밍은 문제가 다음 조건을 만족할 때 사용할 수 있다.

1. 최적 부분 구조 (Optimal Substructure)

: 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결 할 수 있다.

2. 중복되는 부분 문제 (Overlapping Subproblem)

: 동일한 작은 문제를 반복적으로 해결해야 한다.

구현 방법

다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식으로 구성된다.

보텀업 방식 : 반복문 사용
탑다운 방식 : 재귀와 메모이제이션 사용

1. 보텀업 방식 (Bottom-up Approach)

: 가장 작은 하위 문제부터 시작하여, 그 결과를 이용하여 점진적으로 큰 문제의 해결책을 구하는 방식

일반적으로 반복문을 사용하여 구현된다.
보텀업 방식은 계산해야 할 하위 문제의 수가 적은 경우에 유리하다.
모든 하위 문제를 한 번씩만 계산하므로 중복 계산을 피할 수 있다.
보텀업 방식에서 사용되는 결과 저장용 리스트는 DP 테이블이라고 부른다.

구현 절차

가장 작은 하위 문제에 대한 해결책을 계산한다.
작은 하위 문제의 해결책을 이용해 조금 더 큰 문제에 대한 해결책을 계산한다.
위의 단계를 반복하여 큰 문제의 해결책을 계산한다.

2. 탑다운 방식 (Top-down Approach)

: 큰 문제를 해결하기 위해 작은 하위 문제들을 재귀적으로 호출하여 해결하는 방식

일반적으로 재귀 함수를 사용하여 구현된다.
탑다운 방식은 중복 계산이 발생할 수 있다.
하지만 메모이제이션 기법을 사용하여 한 번 계산한 하위 문제의 해결책을 저장하고, 재사용함으로써 중복 계산을 피할 수 있다.

구현 절차

큰 문제를 해결하기 위한 함수를 정의하고, 함수 내에서 작은 하위 문제들을 재귀적으로 호출한다.
작은 하위 문제들을 해결하는 함수를 정의하고, 이 함수도 작은 하위 문제들을 재귀적으로 호출한다.
base case(종료 조건)에 도달하면 작은 하위 문제의 해결책을 반환한다.

메모이제이션 (Memoization)

: 다이나믹 프로그래밍을 구현하는 방법 중 하나로, 한 번 계산한 결과를 메모리 공간에 메모하는 기법

같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져온다.

값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 한다.

예시 - 피보나치 수열

다이내믹 프로그래밍으로 해결할 수 있는 대표적인 문제로는 피보나치 수열이 있다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ...
피보나치 수열을 점화식으로 표현하면 다음과 같다.
a𝑛 = a𝑛₋₁ + a𝑛₋₂ ( 𝑛 번째 피보나치 수는 𝑛₋₁ 번째와 𝑛₋₂ 번째를 더한 것과 같다.)
a₁ = 1 (1번째 피보나치 수는 1이다.)
a₂ = 1 (2번째 피보나치 수는 1이다.)

점화식

: 인접한 항들 사이의 관계식

이러한 점화식을 알게 된다면 𝑛이 얼마나 큰 수가 되더라도 모든 피보나치 수를 구할 수 있다.

실제 프로그래밍 상에서 재귀 함수를 이용해 점화식을 그대로 소스 코드로 옮겨 구현할 수 있다.

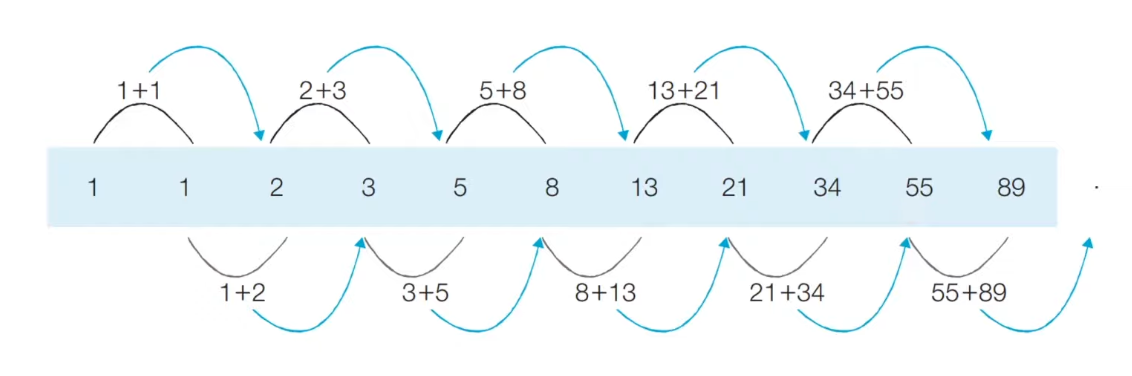
수열(Sequence)은 선형적인 데이터이므로, 프로그래밍에서는 이러한 수열을 표현하기 위해 배열이나 리스트를 사용할 수 있다.

다이나믹 프로그래밍에서도 각각의 계산된 결과를 담기 위해 배열이나 리스트를 사용한다.
값을 별도로 테이블과 같은 공간에 기록한다고 하여, 이러한 배열이나 리스트를 테이블이라고 부르기도 한다.

단순 재귀 코드

피보나치 함수를 단순한 재귀 함수로 구현하면 아래와 같다.

function fibo(n) {
  if (n === 1 || n === 2) return 1; // 재귀함수 종료 조건

  return fibo(n - 1) + fibo(n - 2); // 점화식을 그대로 옮기면 된다.
}

console.log(fibo(9)); // 34

이렇게 단순 재귀 함수로 구현한 피보나치 함수는 지수 시간복잡도O(2ⁿ)를 가지게 된다.

fibo(9)를 계산하기 위해 fibo(1), fibo(2), fibo(3), ...는 여러 번 호출된다. ➡️ 중복되는 부분 문제❗️
위의 코드로 fibo(30)을 계산하려고 한다면, 2³⁰ = 약 10억 가량의 연산을 수행해야 한다..

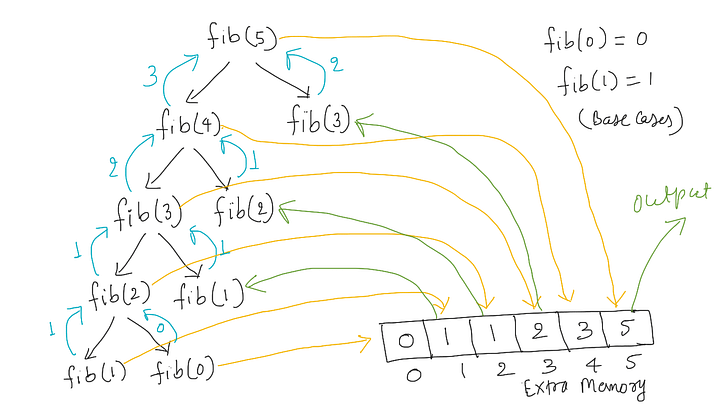
탑다운 다이나믹 프로그래밍 코드

피보나치는 다이나믹 프로그래밍의 사용 조건인 최적 부분 구조와 중복되는 부분 문제를 충족하기 때문에, 다이내믹 프로그래밍을 사용해 해결할 수 있다.

최적 부분 구조 : 큰 문제를 작은 문제로 나눌 수 있다.
중복되는 부분 문제: 동일한 작은 문제를 반복적으로 해결한다.

// 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
function fibo(n) {
  const memo = []; // 한 번 계산한 값을 저장할 메모이제이션 할 배열 (중복 계산 피하기 위해)
  
  if (n === 1 || n === 2) return 1; // 재귀함수 종료 조건
  
  if (memo[n]) return memo[n]; // 이미 계산한 값이라면 메모한 값을 가져와 반환
  
  memo[n] = fibo(n - 1) + fibo(n - 2); // 아직 계산하지 않은 문제라면 점화식에 따라서 계산하고 결과값을 메모
  
  return memo[n];
}

console.log(fibo(9)); // 34

메모이제이션을 이용한 피보나치 함수는 중복 계산을 하지 않기 때문에, 선형 시간복잡도O(n)를 가진다.

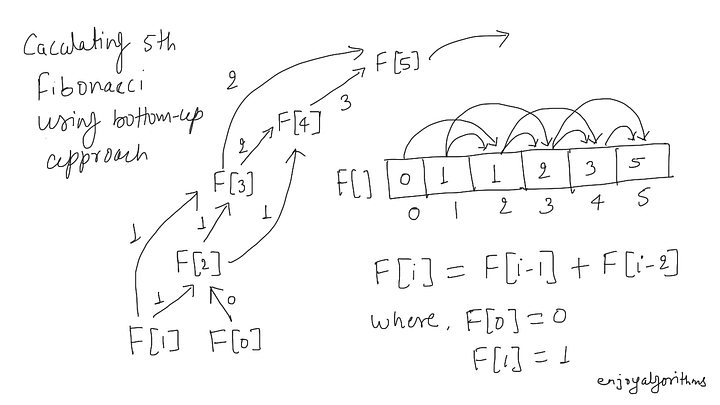
보텀업 다이나믹 프로그래밍 코드

// 반복문으로 구현 (보텀업 다이나믹 프로그래밍)
function fibo(n) {
  const table = []; // DP 테이블
  
  table[1] = 1;
  table[2] = 1;
  
  for (let i = 3; i <= n; i++) { // table에 저장한 값을 이용해 차례대로 1,2,3 ... n번째 피보나치 수까지 구한다.
    table[i] = table[i - 1] + table[i - 2];
  }
  
  return table[n];
}

console.log(fibo(9)); // 34