비교식 정렬

: 다른 요소와 비교를 통해 정렬하는 방식

• 버블 정렬
• 선택 정렬
• 삽입 정렬
  ➡️ 시간 복잡도 O(n²)

분산식 정렬

: 요소를 분산하여 정렬하는 방식

• 병합 정렬
• 퀵 정렬
• 힙 정렬
  ➡️ 시간 복잡도 O(n log n)

분할 정복

: 문제를 작은 2개의 문제로 분리하고, 더 이상 분리가 불가능할 때 처리한 후 합치는 전략

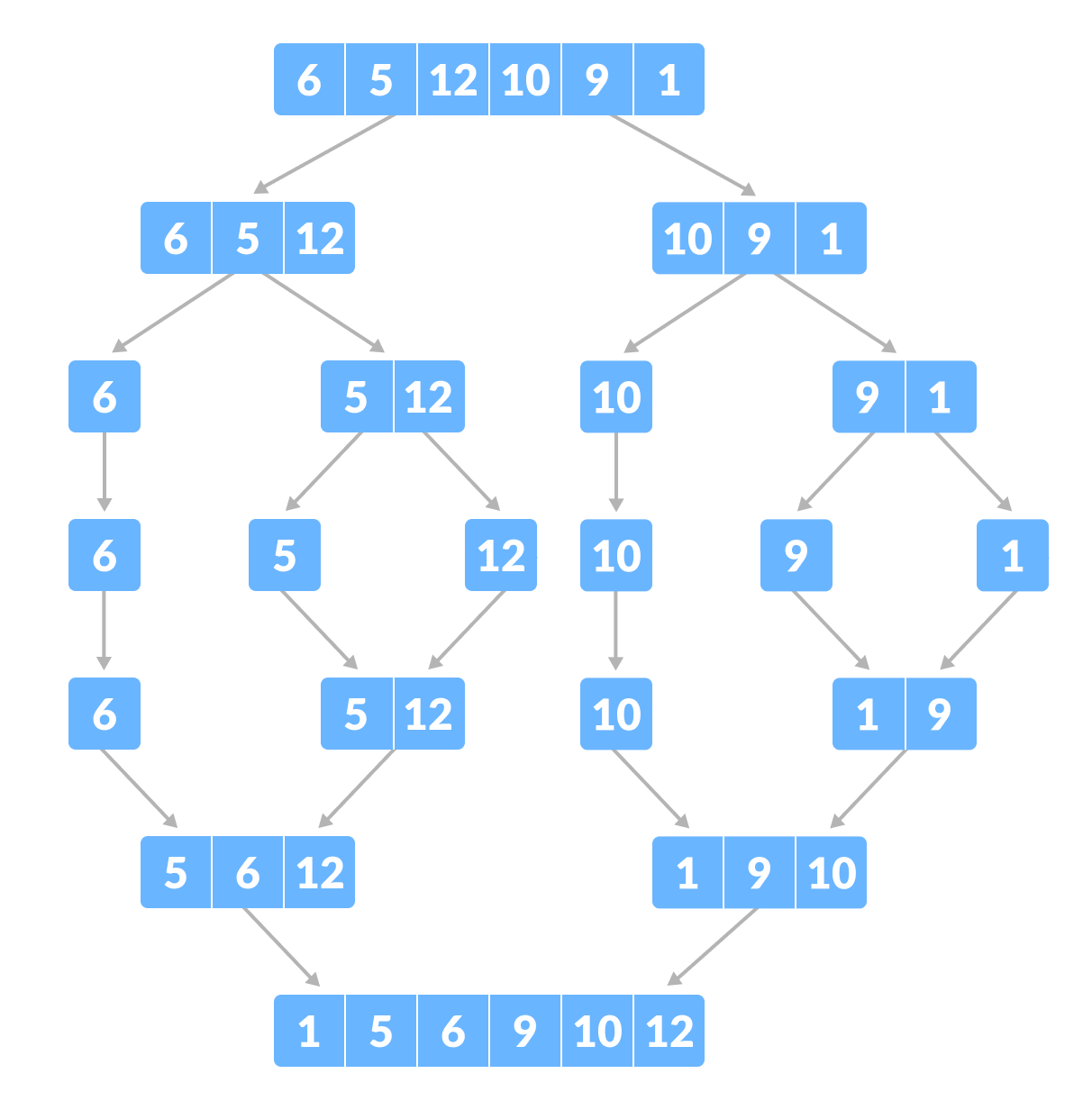
병합 정렬 (Merge Sort)

: 분할 정복 알고리즘을 이용한 최선과 최악이 같은 안정적인 정렬 알고리즘

• 요소들을 절반으로 나눈다. → 분할
• 요소가 하나만 남을 때까지 계속해서 절반으로 나눈다.
• 모든 요소가 나누어졌다면, 합치기 시작한다. → 정복
• 합칠 때, 두 요소 중 작은 요소를 앞에 배치한다.

의사 코드

// 전체 배열을 계속해서 절반으로 나누는 함수 (배열 하나당 요소가 1개씩 될 때까지)
function mergeSort(arr) {
  // 재귀 함수 탈출 조건
  만약 (배열의 길이가 1이 된다면) {
    배열을 리턴한다. // 요소가 1개 남은 배열이 리턴된다.
  }
  
  // 재귀적으로 반복될 코드
  mid = 배열의 중간값
  left = 0부터 mid 앞까지;  // 배열을 절반으로 나눴을 때 왼쪽에 있는 값들
  right = mid부터 끝까지; // 배열을 절반으로 나눴을 때 오른쪽에 있는 값들
  
  쪼갠 왼쪽 배열과 오른쪽 배열을 다시 쪼갠다.
  모든 배열이 요소가 1개씩 남도록 쪼개지면, merge 함수로 전달하여 합친다.
};

// 두 배열의 요소를 오름차순으로 정렬해 하나로 합쳐주는 함수
function merge(left, right) { 
  정렬된 배열을 담을 변수 sortedArr를 만든다.
    
  반복문 (left 배열과 right 배열 둘 중 하나라도 빈 배열이 될 때까지) {
    각 배열의 맨 왼쪽(제일 작은 수)끼리 비교한다.
    만약 (left[0]이 right[0]보다 작다면) {
      sortedArr에 left[0]을 추가하고, left 배열에서 삭제한다.
    } 만약 right[0]이 더 작다면 {
     sortedArr에 right[0]을 추가하고, right 배열에서 삭제한다.
    }
  }
  left나 right 배열 중 하나가 빈 배열이 되어서,
  반복문이 끝나면, [...sortedArr, ...left, ...right]를 리턴한다. // 이때 완전히 정렬된 배열이 만들어진다.
};

풀이

function mergeSort(arr) {
  // base case
  if (arr.length < 2) {
    return arr;
  }
  
  // recursive case
  const mid = Math.floor(arr.length / 2);
  const left = arr.slice(0, mid);
  const right = arr.slice(mid);
  
  return merge(mergeSort(left), mergeSort(right));
} // O(log n) 

function merge(left, right) { 
  const sortedArr = [];
  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      sortedArr.push(left.shift());
    } else {
      sortedArr.push(right.shift());
    }
  }
  
  return [...sortedArr, ...left, ...right];
} // O(n)

병합 정렬은 O(n log n)의 시간 복잡도를 가진다.

이 글은 아래 링크를 참고하여 작성한 글입니다.
JavaScript Algorithms - 27 - Merge Sort Solution