퀵 정렬 (Quick Sort)

: 분할 정복 알고리즘을 이용한 매우 빠르지만 최악의 경우에는 이차 시간 O(n²)이 소요될 수도 있는 불안정 정렬 알고리즘

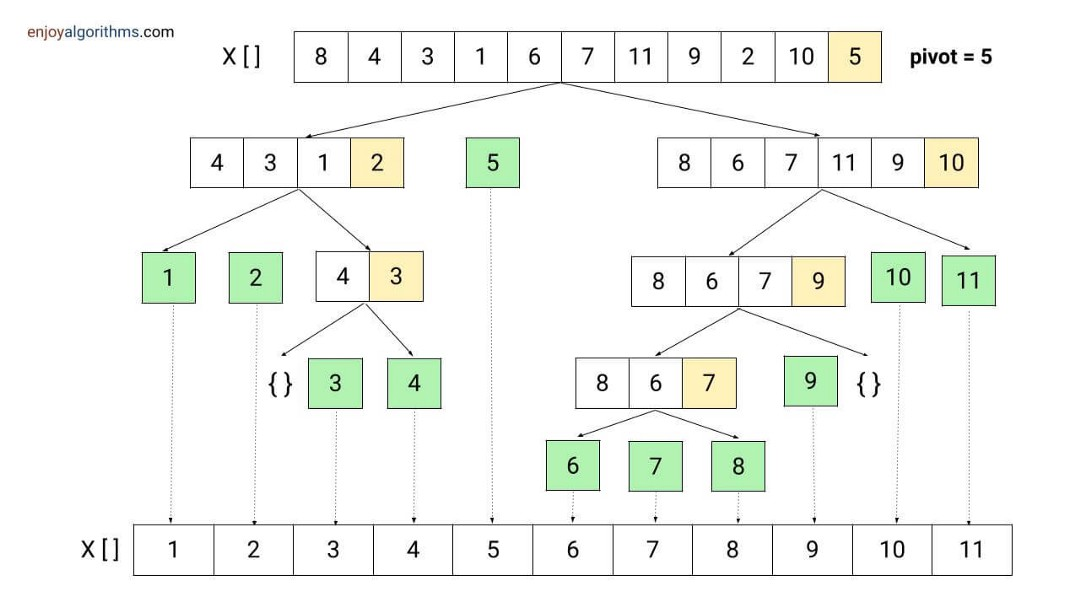
• 마지막 요소가 Pivot이 된다.
  Pivot을 기준으로 Pivot보다 작으면 좌측, Pivot보다 크면 우측으로 나눈다. → 분할
• 나뉜 요소에서 다시 마지막 요소가 Pivot이 된다. Pivot을 기준으로 다시 좌측과 우측으로 나눈다.
• 더 이상 나눌 수 없는 상태가 되면 그대로 합쳐준다. → 정복

의사 코드

function quickSort(arr) {
  // 재귀 함수 탈출 조건
  만약 (배열의 길이가 1이 된다면) {
    배열을 리턴한다. // 요소가 1개 남은 배열이 리턴된다.
  }
  
  // 재귀적으로 반복될 코드
  pivot = 맨 뒤의 요소
  left = []; // pivot보다 작은 요소들을 담을 배열
  right = []; // pivot보다 큰 요소들을 담을 배열
  
  반복문 (pivot을 제외한 나머지 요소를 순회) {
    만약 (요소가 pivot보다 작다면) {
      left 배열에 넣는다.
    } 요소가 pivot보다 크다면 {
      right 배열에 넣는다.
    }
  }
  
  재귀를 이용해서 left, right 배열을 다시 quickSort 함수에 넣는다.
  return [...quickSort(left), pivot, ...quickSort(right)]
}

풀이

function quickSort(arr) {
  // base case
  if (arr.length < 2) {
  	return arr;
  }
  
  // recursive case
  let pivot = arr[arr.length - 1];
  let left = [];
  let right = [];
  
  for (let i = 0; i < arr.length - 1; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  } // O(n)
  
  return [...quickSort(left), pivot, ...quickSort(right)]; // O(log n)
}

퀵 정렬은 O(n log n)의 시간복잡도를 가진다.

이 글은 아래 링크를 참고하여 작성한 글입니다.
JavaScript Algorithms - 25 - Quick Sort Solution