이진 탐색의 특징
- 반드시 정렬이 되어있어야 사용할 수 있다.
- 배열 또는 이진 트리를 이용하여 구현할 수 있다.
O(log N)의 시간 복잡도로 탐색 속도가 상당히 빠르다.
이진 탐색 트리 (Binary Search Tree)
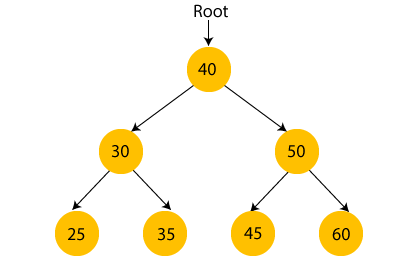
이진 탐색을 위한 이진 트리로, 왼쪽의 서브트리는 루트보다 작은 값이 모여있고, 오른쪽의 서브트리는 루트보다 큰 값이 모여있다.
JavaScript로 이진 탐색 트리 구현하기
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
// 루트가 비어있는 경우
if (this.root === null) {
this.root = newNode;
return;
}
// 루트가 비어있지 않은 경우
let currentNode = this.root; // 루트 노드부터 탐색 시작
while (currentNode !== null) {
// 현재 탐색중인 노드보다 newNode의 값이 큰 경우 -> 오른쪽
if (currentNode.value < value) {
if (currentNode.right === null) { // 현재 노드의 오른쪽 자식이 비었다면
currentNode.right = newNode; // 현재 노드의 오른쪽 자식 자리에 넣는다.
break; // 반복문 탈출
}
currentNode = currentNode.right; // 현재 노드의 오른쪽 자식이 채워져있다면, 오른쪽 자식을 탐색한다.
// 현재 탐색중인 노드보다 newNode의 값이 작은 경우 -> 왼쪽
} else {
if (currentNode.left === null) { // 현재 노드의 왼쪽 자식이 비었다면
currentNode.left = newNode; // 현재 노드의 왼쪽 자식 자리에 넣는다.
break; // 반복문 탈출
}
currentNode = currentNode.left; // 현재 노드의 왼쪽 자식이 채워져있다면, 왼쪽 자식을 탐색한다.
}
}
}
has (value) {
let currentNode = this.root; // 루트 노드부터 탐색 시작
while (currentNode !== null) {
if (currentNode.value === value) { // 찾았으면 true 리턴
return true;
}
if (currentNode.value < value) { // 현재 노드보다 찾는 값이 크다면
currentNode = currentNode.right; // 오른쪽 자식을 탐색한다.
} else { // 현재 노드보다 찾는 값이 작다면
currentNode = currentNode.left; // 왼쪽 자식을 탐색한다.
}
}
return false; // 순회를 다 했는데 못찾았다면 false 리턴
}
}예시
const tree = new BinarySearchTree();
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
tree.insert(2);
console.log(tree.has(8)); // true;
console.log(tree.has(1)); // false;위의 트리를 그림으로 나타내면 아래와 같다.

이진 트리 순회 알고리즘
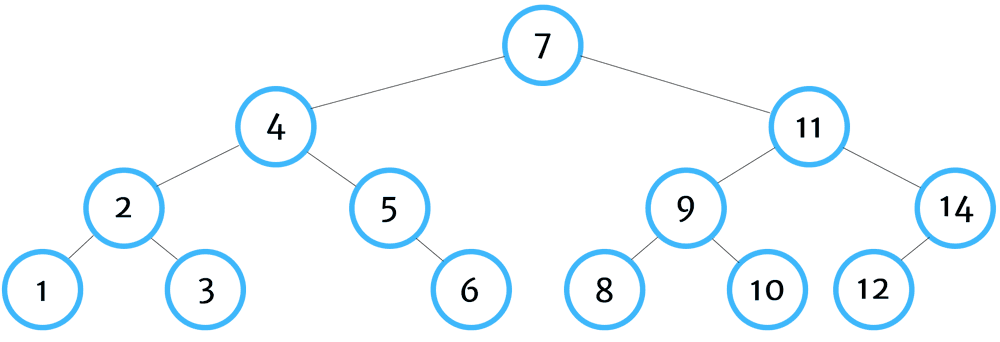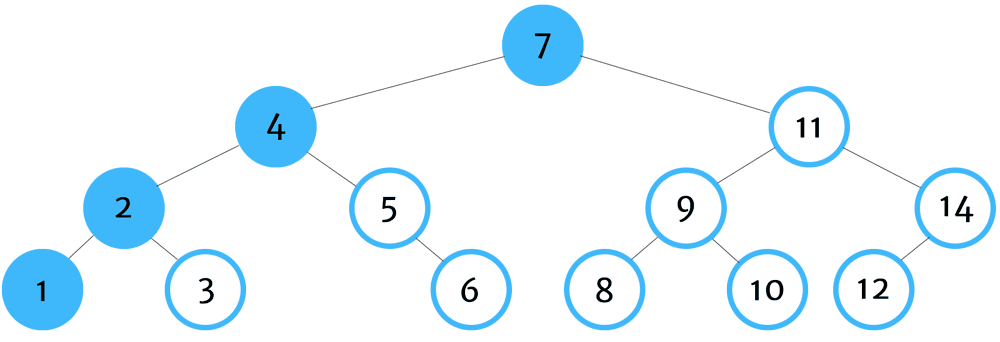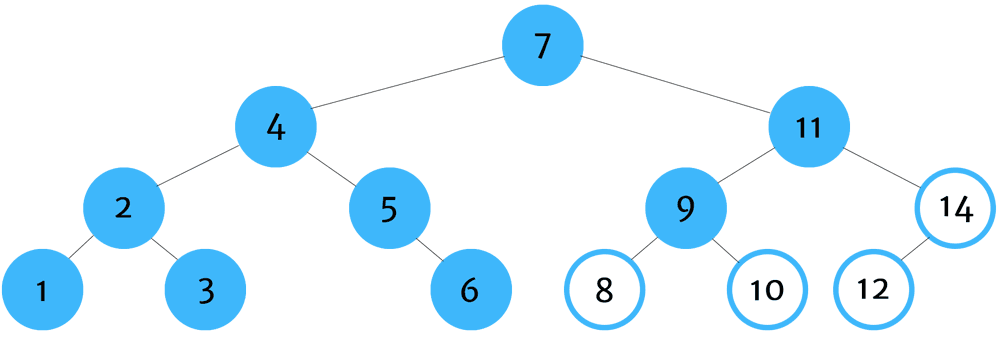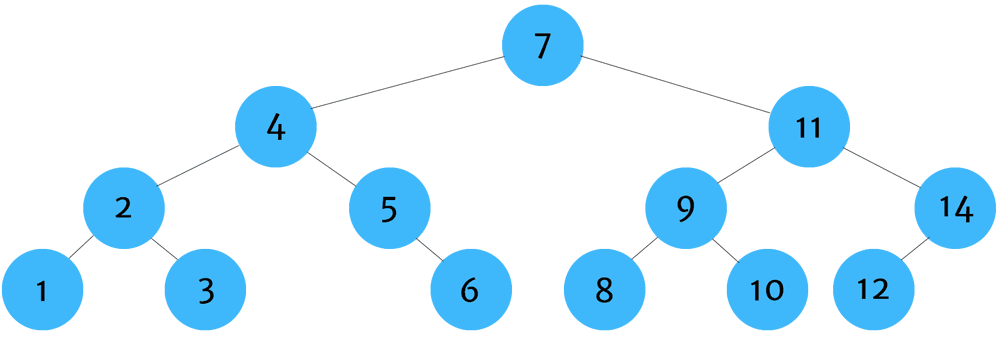
전위 순회 (Pre-Order Traversal)
: 노드에 방문했을 때, 자기 자신 → 왼쪽 자식 → 오른쪽 자식을 처리하는 탐색 방법

class BinarySearchTree {
// ...생략
preOrder(node) {
console.log(node.value);
node.left && this.preOrder(node.left);
node.right && this.preOrder(node.right);
}
}예시
아래의 트리에서 tree.preOrder(tree.root) 해보면 5, 4, 2, 5, 7, 6, 8 이 순서대로 콘솔에 찍힌다.

중위 순회 (In-Order Traversal)
: 노드에 방문했을 때, 왼쪽 자식 → 자기 자신 → 오른쪽 자식을 처리하는 탐색 방법
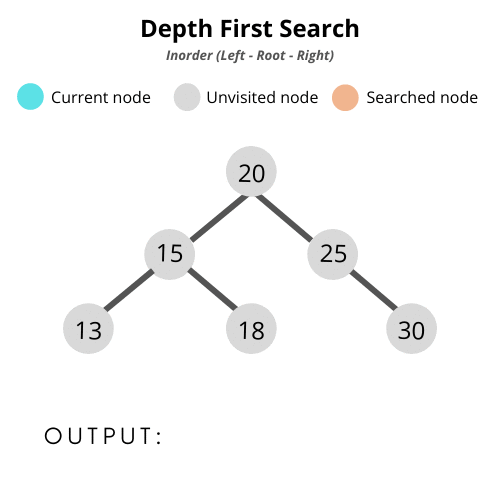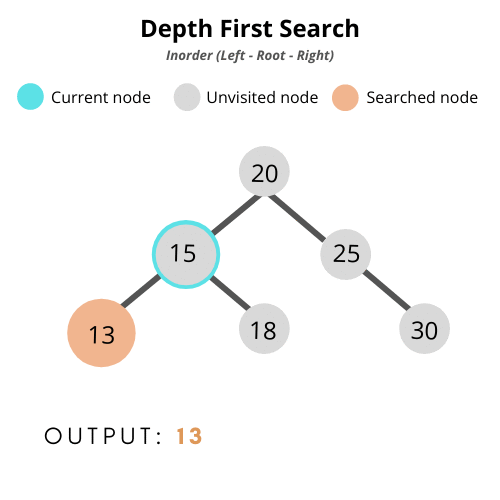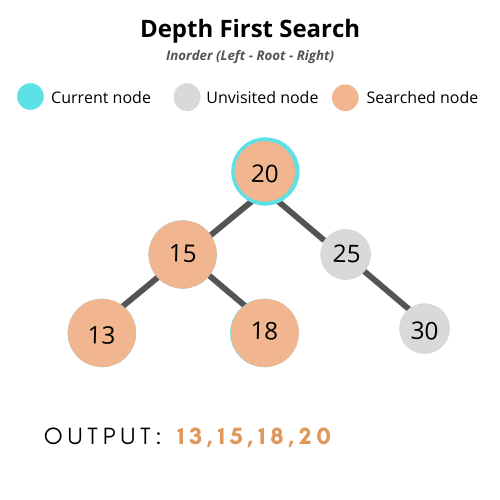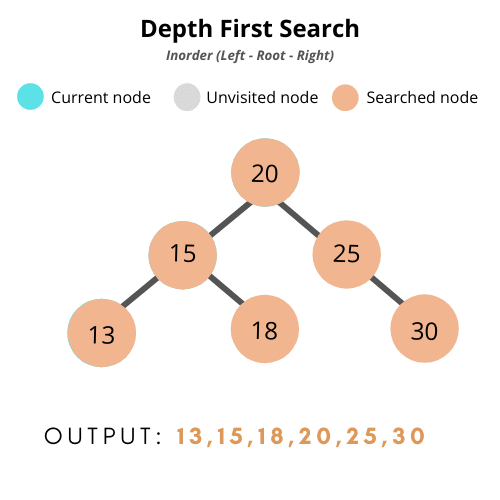
class BinarySearchTree {
// ...생략
inOrder(node) {
node.left && this.inOrder(node.left);
console.log(node.value);
node.right && this.inOrder(node.right);
}
}예시
아래의 예시에서 만든 트리에서 tree.inOrder(tree.root) 해보면 2, 4, 5, 5, 6, 7, 8 이 순서대로 콘솔에 찍힌다.

후위 순회 (Post-Order Traversal)
: 노드에 방문했을 때, 왼쪽 자식 → 오른쪽 자식 → 자기 자신을 처리하는 탐색 방법
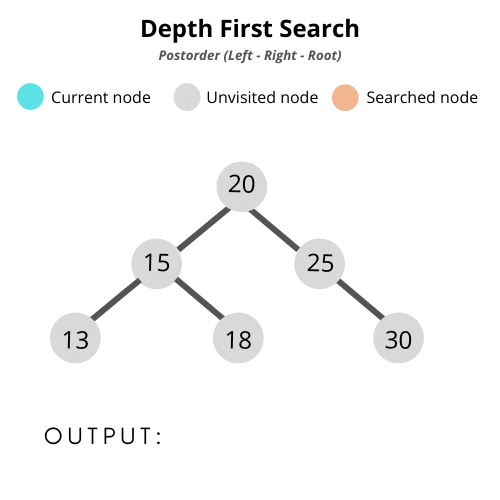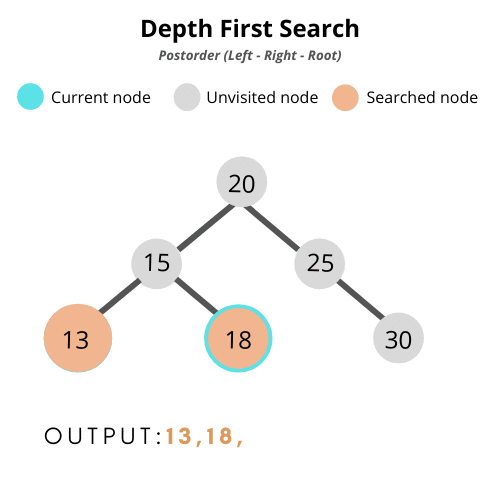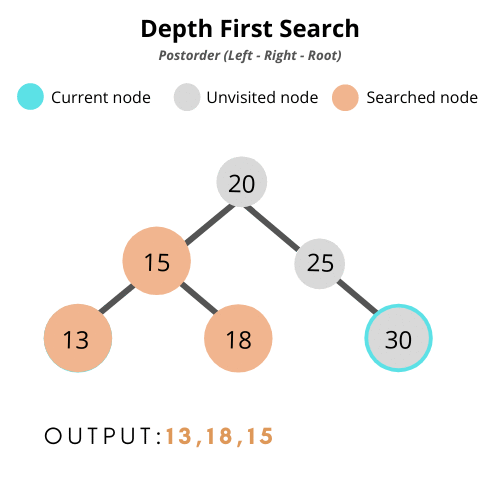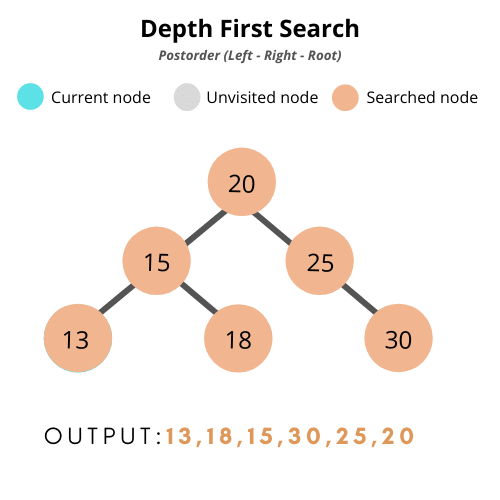
class BinarySearchTree {
// ...생략
postOrder(node) {
node.left && this.postOrder(node.left);
node.right && this.postOrder(node.right);
console.log(node.value);
}
}예시
아래의 예시에서 만든 트리에서 tree.postOrder(tree.root) 해보면 2, 5, 4, 6, 8, 7, 5 가 순서대로 콘솔에 찍힌다.

이 글은 아래 링크를 참고하여 작성한 글입니다.
https://levelup.gitconnected.com/how-to-traverse-a-tree-using-javascript-c9a79826e819






이진탐색.... 머리 아픕니다.. 그치만 정리가 넘 잘돼있네용 잘보고가요 ㅎㅎ