[알고리즘] 시간복잡도(TimeComplexity)

| 시간복잡도 학습에 앞서 궁금했던 점
예를들어, log100인 경우 log의 밑을 10인 상용로그로 가정하는데, 왜 시간 복잡도에선 log100을 6.64, 대략 7번 정도로 판단하는지 이해가 안갔다. 그래서 찾아본 결과 컴퓨터는 0과 1로 이루어진 이진 시스템이기 때문에 일반수학과 달리 log의 밑을 2로 생각한다고 한다.

🪄Tip

• 컴퓨터 과학에서 로그의 밑은 2로 간주
  (알고리즘의 시간복잡도를 분석할 때 사용되는 관례)
• 컴퓨터는 0과 1루어진 이진 시스템을 사용
  따라서, 컴퓨터 연산은 2진수로 처리
  이에따라, 알고리즘의 시간복잡도를 분석할 때, 자주 사용되는 데이터 구조 중 하나인 이진트리(Binary Tree)등과 같은 구조를 고려할 시 로그의 밑을 2로 간주한다.

---

시간 복잡도(TimeComplexity)

=> 알고리즘 선택의 기준이 된다.
=> 주어진 문제를 해결하기 위한 연산 횟수
=> 일반적으로 수행 시간은 1억번의 연산을 1초의 시간으로 간주하여 예측한다.

시간 복잡도 정의하기

• 빅-오메가(Ω(n)) : 최선일 때(best case)의 연산 횟수를 나타낸 표기법
  
  
• 빅-세타(θ(n)) : 보통일 때(average case)의 연산 횟수를 나타낸 표기법
  
  
• 빅-오(O(n)) : 최악일 때(worst case)의 연산 횟수를 나타낸 표기법
  => 코딩 테스트에서는 항상 최악의 케이스(빅-오)를 염두에 두고 임해야 한다.
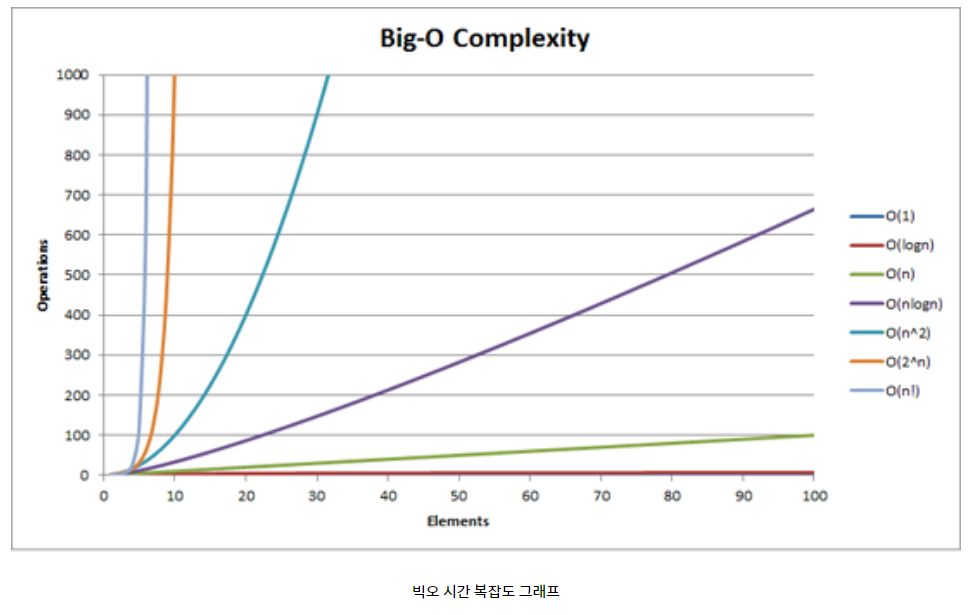
  => 다양한 테스트 케이스를 수행해 모든 케이스를 통과해야하기 때문이다.

                          빅-오(O(n)) 시간 복잡도 그래프

- Operation : 수행 속도
- Elemets : 데이터 크기

그래프 출처 : https://devhwan.me/61

---

시간 복잡도를 고려한 연산 횟수 계산

연산 횟수 = (알고리즘 시간 복잡도) * (데이터의 크기)

=> 시간 복잡도는 항상 최악일 때,
   즉, 데이터의 크기가 가장 클 때를 기준으로 한다.

---

EX1)
[백준]2750번 | 시간 제한:2초
(주어진 시간 제한이 2초이기 때문에, 2억번의 연산 안에 값을 출력할 수 있어야 한다!(1초는 약 1억번의 연산))

N개의 수가 주어졌을 때 이를 오름차순 정렬하는 프로그램을 작성하시오.

| 입력
//고려해야 할 데이터 크기=1,000,000(가장 큰 값)
1번째 줄에 수의 갯수(1<=N<=1,000,000) 2번째 줄부터는~

|출력
1번째 줄부터 N개의 줄에 오름차순 정렬한 결과를~

• 해당 문제에 대한 시간 복잡도는 어떻게 생각해야 할까?

  => 최대 데이터 크기 1,000,000(백만)

• 해당 문제 알고리즘 적합성 평가

  • 버블 정렬(N^2)
    : (1,000,000)^2=1,000,000,000,000>200,000,000(2억번)
    => 부적합 알고리즘
     : 주어진 시간 2초보다 더 큰 시간동안 연산을 수행하므로 시간초과 발생

  • 병합 정렬(NlogN)
    : 1,000,000log(1,000,000)=약 20,000,000<200,000,000
    => 적합 알고리즘
     : 주어진 시간보다 적은 연산 횟수로 값 도출 가능(약 0.2초 만에 수행)

  ---

  시간 복잡도 도출 기준

  1) 상수는 시간 복잡도 계산에서 제외한다.
  2) 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.

1) 상수는 시간 복잡도 계산에서 제외한다.

• 연산 횟수가 N인 경우

EX1) 
public class 시간복잡도_판별원리1{
  public static void main(String [] args){
	int N=100000;
	int cnt=0;
	for(int i=0; i<N; i++){ //N번
	  System.out.println("연산 횟수:" + cnt++);
	}
  }
}

• 연산 횟수가 3N인 경우

public class 시간복잡도_판별원리2{
  public static void main(String [] args){
	int N=100000;
	int cnt=0;
	for(int i=0; i<N; i++){ //10만번
	  System.out.println("연산 횟수:" + cnt++);
	}
	for(int i=0; i<N; i++){ //10만번
	  System.out.println("연산 횟수:" + cnt++);
	}
	for(int i=0; i<N; i++){ //10만번
	  System.out.println("연산 횟수:" + cnt++);
	}
  }
}
// 총 30만번의 연산을 하지만, 시간 복잡도에서 상수는
// 계산에 큰 영향도가 없기에 제외한다.

=> 결국 1번 예제나, 1-1번 예제는 코딩테스트에서 큰 차이가 없으며, 상수를 제외시키므로 두 예제의 시간 복잡도는 O(n)으로 동일하다.
=> 시간 복잡도는 주로 입력 크기에 따른 알고리즘의 성장 추세를 이해하는 데에 초점을 맞추고 있으며, 이런 맥락에서는 상수 계수의 영향력을 무시하고 알고리즘들을 비교하는 것이 일반적

ex) N이 1억이나 1조와 같이 매우 큰 값이 될 때는 상수 계수의 영향력이 작아져서 둘 사이의 성능 차이가 미미해질 수 있기 때문에

2) 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.

• 연산 횟수가 N^2인 경우

public class 시간복잡도_판별원리3 {
  public static void main(String [] args){
	int N=100000;
	int cnt=0;
	for(int i=0; i<N; i++){ // N번
	  for(int j=0; j<N;j++){ // N번
	  System.out.println("연산 횟수:" + cnt++);
	}
	}
  }
}

=> for문이 N번씩 2번 돌리는 이중 포문이므로 O(N^2)
=> 만약 일반 for문이 10개 더 있다 하더라도, 시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하므로 해당 코드에서는 이중 for문이 전체 코드의 시간복잡도 기준이 된다.

---

| 결론
맞는 알고리즘을 구현했음에도 불구하고 시간 초과가 발생했다면,
시간 복잡도의 원리를 통해 문제가 되는 코드 부분을 도출하여 효율적인 구조로 수정해 문제를 해결할 수 있다.

1) 알맞은 알고리즘 사용하기
(시간 복잡도를 잘 따질 줄 알아야한다.)
2) 비효율적인 로직을 찾아서 효율적으로 변경하기
-> 가장 시간 복잡도를 크게 잡아먹는 부분을 먼저 파악한다.

| 내가 푼 시간 복잡도 문제
백준 24265

참고 : Do it! 알고리즘 코딩 테스트 자바편