동적 프로그래밍이란?
동적 프로그래밍은 큰 문제를 풀 때, 큰 문제의 일부인 작은 문제를 푸는 과정에서 발생하는 중복을 해결하는 방법이다.
이때 큰 문제의 해답에 그보다 작은 문제의 해답이 포함되어 있는 것을 최적 부분 구조(Optimal Substructure)를 가졌다고 표현한다.
대표적인 예시로 피보나치 수열이 있다.
피보나치 수열은 다음의 정의를 갖는다.
f(n) = f(n-1) + f(n-2)
f(1) = f(2) = 1
즉, n은 n-1과 n-2 피보나치 수를 모두 갖고 있다.
만약 이 문제를 재귀호출로 푼다면 어떨까?
fib(n)
{
if (n == 1 or n == 2)
then return 1
else return (fib(n-1) + fib(n-2))
}이렇게 푸는 방식은 매우 비효율적인 방식이다.
예를들어, fib(5)를 구하면 fib(1)과 fib(2)도 중복으로 계산해야 한다.
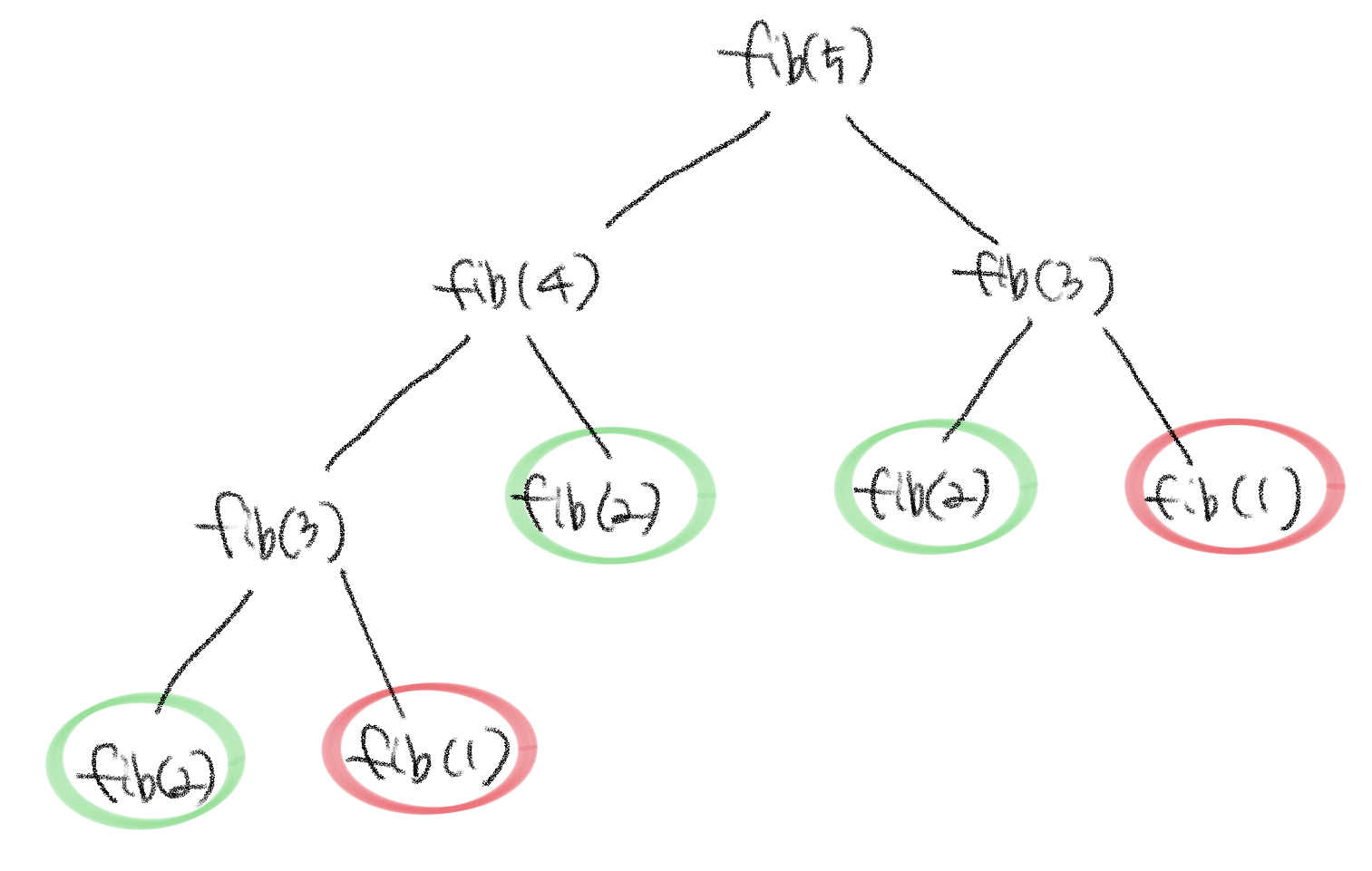
숫자가 더 커진다면 중복 호출의 정도는 더 심해질 것이다.
만약 fib(3)을 매번 호출하지 않고, 실행 결과를 잠시 저장해두고 필요할 때 사용하는 것은 어떨까?
이렇게 부분 결과를 저장해두고 사용하는 것이 동적 프로그래밍의 핵심이다.
또 중복 호출로 인해 비효율적인 연산을 여러번 발생하는 경우는 동적 프로그래밍을 사용하기 적합한 예시다.
동적 프로그래밍 구현하기
bottom-up
아래에서 위로 저장해가면서 해를 구하는 것을 말한다.
fibo(n)
{
f[1] <- f[2] <- 1;
for i <- to n
f[i] <- f[i-1] + f[i-2];
return f[n];
}top-down
중복된 재귀호출을 피하기 위해 한 번 호출한 것을 메모해두고 사용하는 방식을 말한다. 이때 메모하는 행위를 Memoization이라고 한다.
fibo(n)
{
if(f[n] != 0) then return f[n];
else {
if (n = 1 or n = 2)
then f[n] <- 1
else f[n] <- fib(n-1) + fib(n-2);
return f[n];
}
}동적 프로그래밍 적용 예시
대표적인 동적 프로그래밍 문제를 살펴보자.
P9465. 스티커
이 문제는 스티커를 떼어낼 때마다 점수를 매길 때, 점수의 최댓값을 구하는 것이다.
스티커를 떼어낼 때 제한 조건은 다음과 같다.
- 스티커 한 장을 떼면, 그 스티커와 변을 공유하는 스티커는 뗄 수 없다.
이러한 제약 조건을 고려하여 노란색 별이 표시된 스티커를 제거한다면, 1) 직전에 스티커를 제거한 경우와 2) 직전에 스티커를 제거하지 않은 경우 를 확인할 수 있다. 이때 두 가지 경우에서 더 큰 경우를 저장하는 것이다.
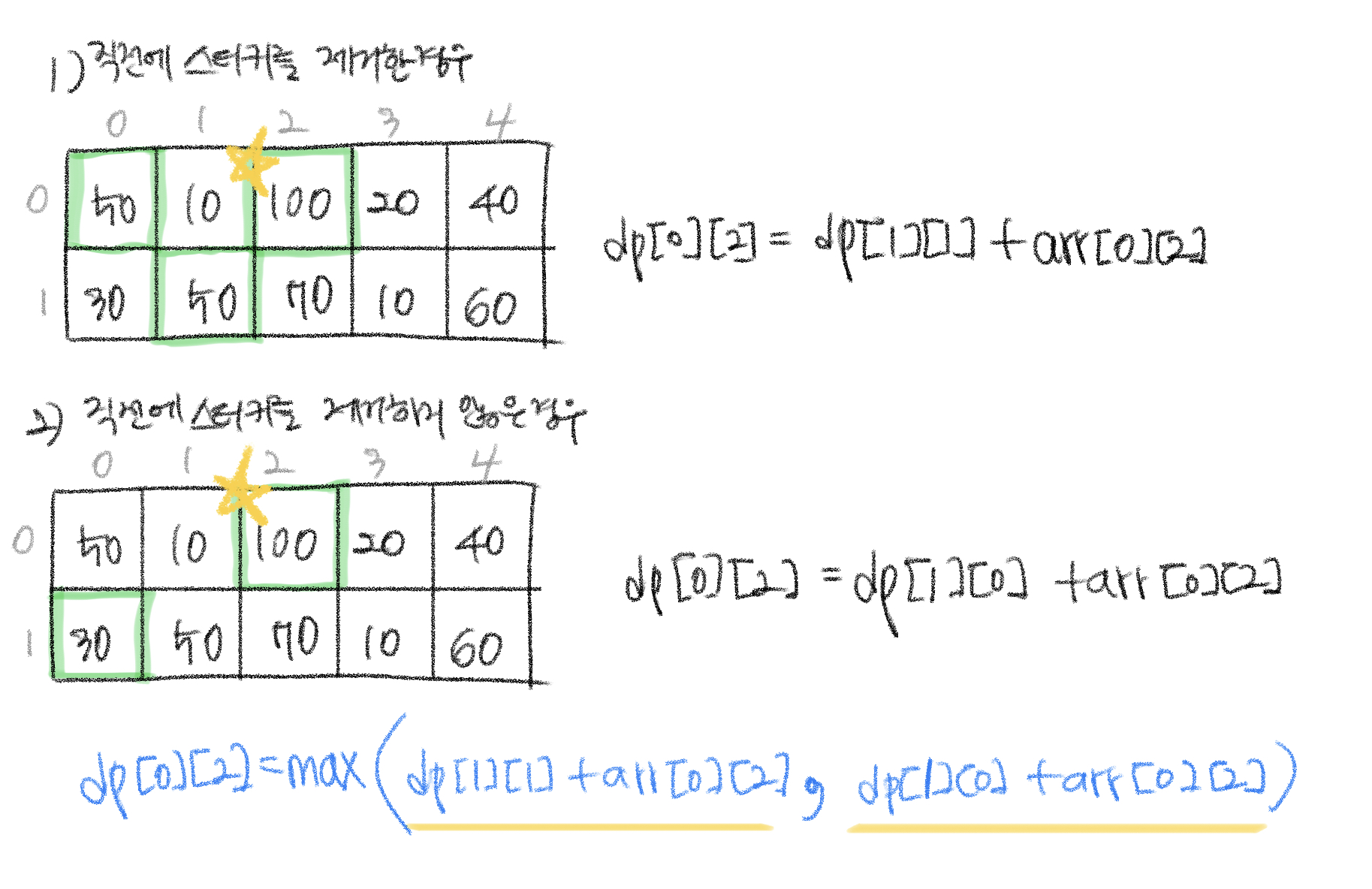
빨간색 별도 마찬가지다.

이 규칙을 재귀적으로 나타내면 다음과 같다.
dp 배열은 큰 해를 구하기 위해 계산한 작은 문제들을 저장하는 최적 부분 구조 배열이고, arr 배열은 스티커 점수를 저장한다.
만약 i가 1이라면,
dp[0][0] = arr[0][0]
dp[1][0] = arr[1][0]
i가 2라면
dp[0][1] = dp[1][0] + arr[0][1]
dp[1][1] = dp[0][0] + arr[1][1]
i가 3 이상이라면
dp[0][i] = max(dp[1][i-1] + arr[0][i], dp[1][i-2] + arr[0][i])
dp[1][i] = max(dp[0][i-1] + arr[1][i], dp[0][i-2] + arr[1][i])
이렇게 스티커를 떼어가다가 최종적으로 dp[0][n-1]과 dp[1][n-1] 중에 더 큰 것이 답이다.
⭐️ 코드
t = int(s.readline())
for i in range(t):
n = int(s.readline())
arr = [list(map(int, s.readline().split())), list(map(int, s.readline().split()))]
for k in range(1, n):
# 두번째 값까지는 대각선 값 더해주기
if k == 1:
s[0][k] += s[1][k-1]
s[1][k] += s[0][k-1]
# 세번째 값부터 대각선과 대각선 왼쪽을 살펴본다.
else:
s[0][k] += max(s[1][k-1], s[1][k-2])
s[1][k] += max(s[0][k-1], s[0][k-2])
print(max(s[0][n-1], s[1][n-1]))P9084. 동전
이 문제는 여러 단위의 주어진 동전을 가지고, 목표 금액을 만들 수 있는 경우의 수를 구하는 것이다.
예를들어, 2원과 4원으로 10원을 만들어보자.
첫번째로 2원만 사용하겠다.
2원으로 0원을 만드는 방법은 2원이 0개만 있으면 되기 때문에 방법이 한 가지이다.

다음은 2원과 4원을 함께 사용한다.

2원과 4원을 가지고 8원을 만드는 방법은 다음과 같다.
- 2 + 2 + 2 + 2
- 2 + 2 + 4
- 4 + 4
일단 8원에서 내가 가진 4원을 뺀 나머지 금액인 4원으로 만들 수 있는 가지수를 확인하는 것이다.
즉, dp[8] = dp[8-4] = dp[4]가 되어 dp 테이블에서 인덱스 4 값을 갖는다.
2원만 가지고 만들 수 있는 경우의 수는 1가지이고, 2원과 4원을 함께 사용하여 만들 수 있는 경우의 수는 2가지 이므로 총 3가지 경우의 수를 갖는다.
⭐️ 코드(2차원)
from sys import stdin as s
import sys
T = int(s.readline())
dp = [0]*10001
for _ in range(T):
N = int(s.readline())
coins = list(map(int, s.readline().split()))
M = int(s.readline())
dp = [[0] * (M + 1)for _ in range(N + 1)]
for i in range(N + 1):
dp[i][0] = 1
for j in range(1, N + 1):
for k in range(1, M + 1):
dp[j][k] = dp[j - 1][k]
if k - coins[j - 1] >= 0:
dp[j][k] += dp[j][k - coins[j - 1]]
print(dp[N][M])⭐️ 코드(1차원)
앞에서 계산한 동전 단위로 만들 수 있는 경우의 수를 모두 기억하지 않고, 값을 업데이트해도 된다.
from sys import stdin as s
import sys
T = int(s.readline())
dp = [0] * 10001
for _ in range(T):
N = int(s.readline())
coins = list(map(int, s.readline().split()))
M = int(s.readline())
dp = [0] * (M + 1)
dp[0] = 1
for coin in coins:
for i in range(1, M + 1):
if i >= coin:
dp[i] += dp[i - coin]
print(dp[M])P9251. LCS
LCS(Longest Common Subsequence)는 두 문자열에 공통적으로 나타나는 부분 순서를 말한다.
두 문자열을 살펴보자.
- ACAYKP
- CAPCAK
LCS 문제의 최적 부분 구조는 다음과 같다.
두 수열을 X, Y라고 하고 X 수열 인덱스를 m, Y 수열 인덱스는 n이다.
이때 1) X[m]과 Y[n]이 같은 경우와 2) 그렇지 않은 경우에 따라 LCS 길이는 다르게 업데이트된다.
1) X[m]과 Y[n]이 같은 경우
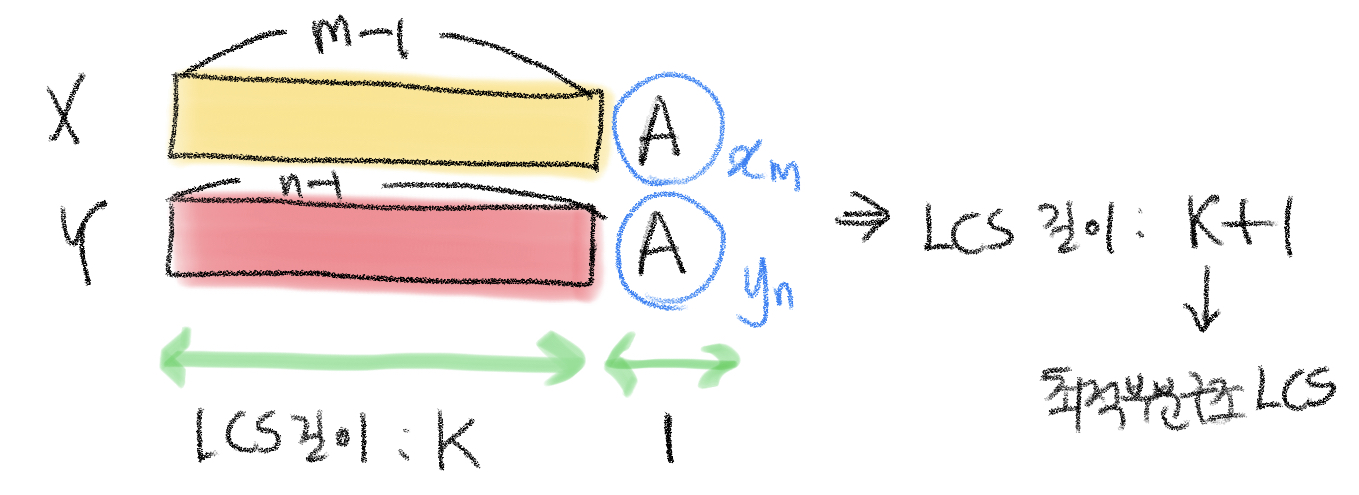
2)X[m]과 Y[n]이 다른 경우
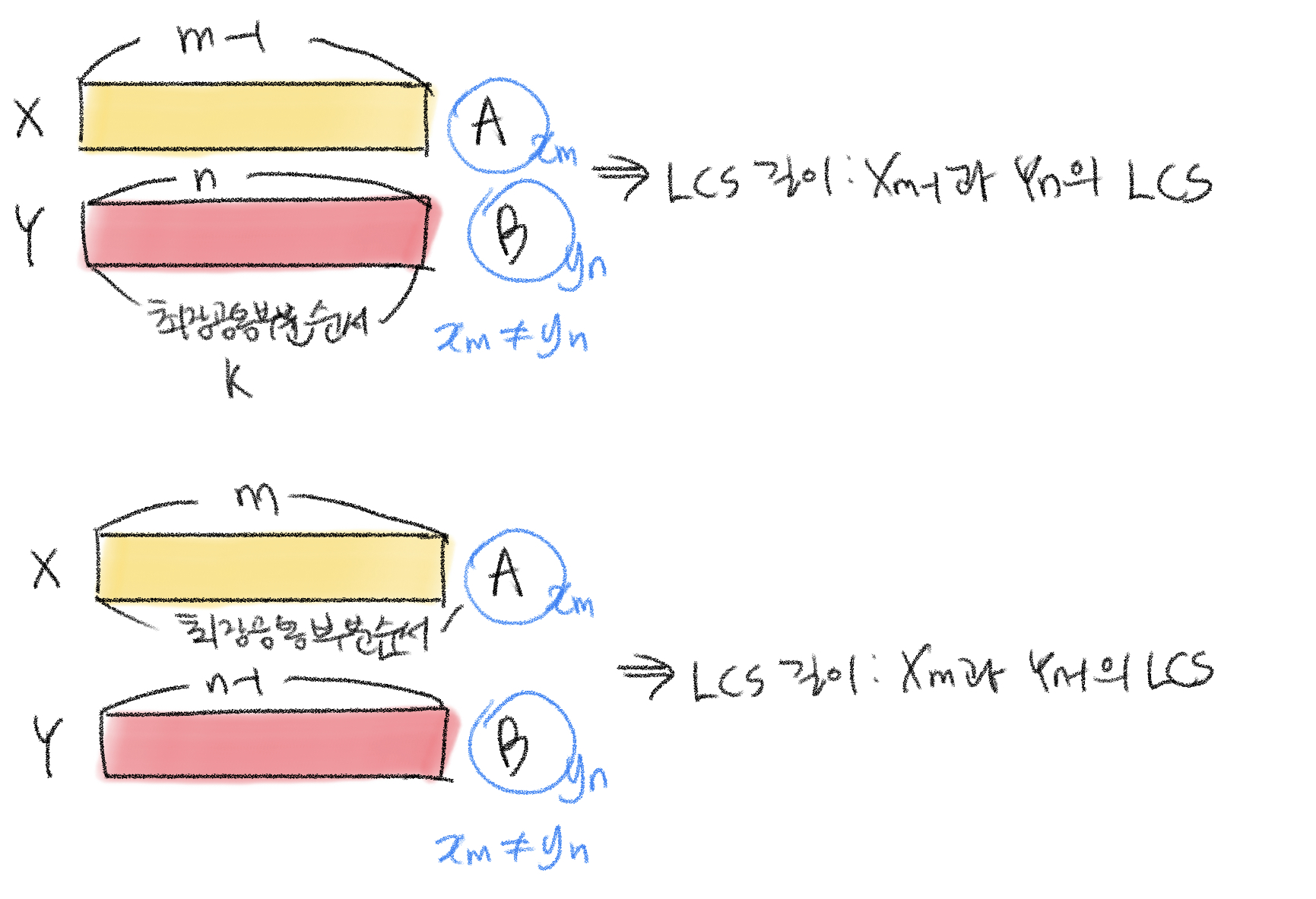
이를 점화식으로 표현하면 다음과 같다.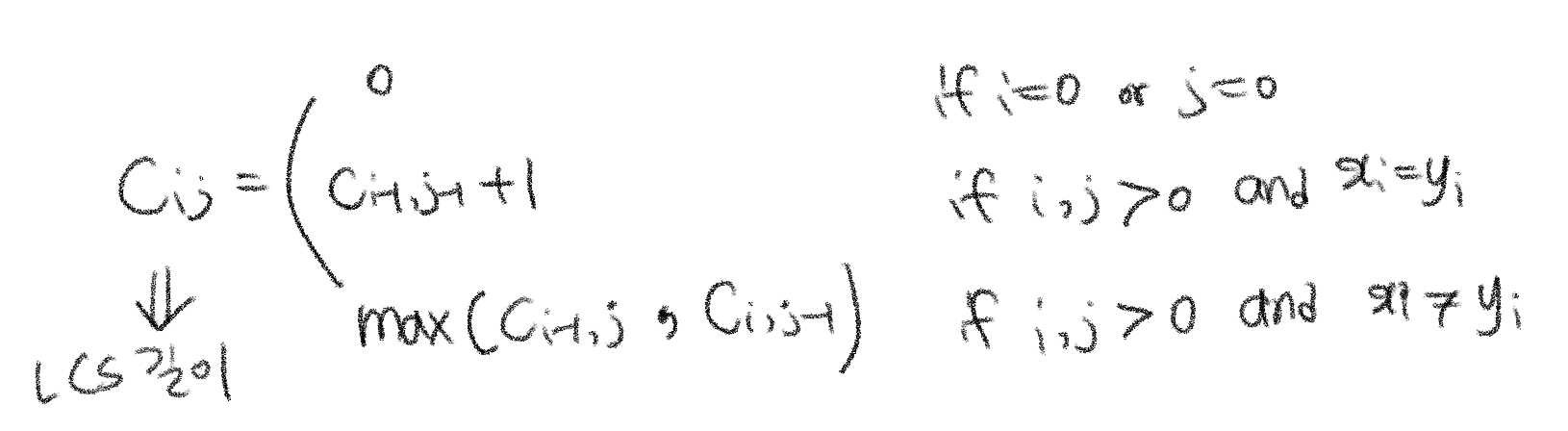
그럼 두 수열을 비교하는 과정을 2차원 배열을 이용해 풀이하겠다.
다음은 위에서 구한 점화식이 반영된 2차원 배열이다. 이차원 배열의 부분 문제의 답을 저장하면서 풀이하여 나온 배열의 가장 마지막 원소인 dp[m][n]이 답이 된다.
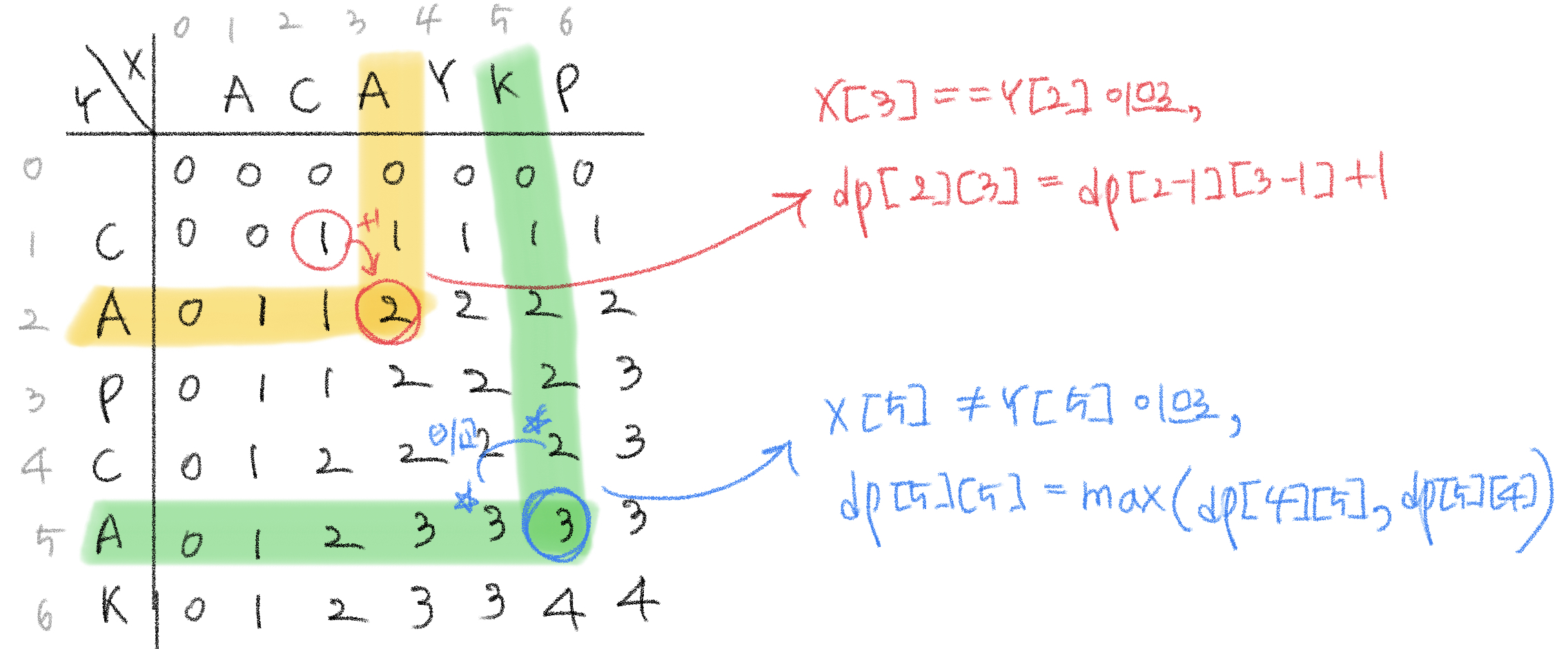
⭐️ 코드
from sys import stdin as s
import sys
a = s.readline().rstrip()
b = s.readline().rstrip()
n = len(a)
m = len(b)
dp = [[0 for _ in range(m+1)] for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
if a[i-1] == b[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else: # 다르다면
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
for i in dp:
print(*i)
print(dp[n][m])P11049. 행렬 곱셈 순서
행렬은 행렬의 결합 법칙에 의해 어떤 순서로 계산을 해도 연산 결과가 같다.
이 문제 예시처럼 A의 크기가 5x3이고, B의 크키가 3x2, C의 크기가 2x6인 행렬곱을 계산하면,
- AB X C 연산 횟수는
(AB의 행렬 연산) + (AB 행렬 연산 결과) X C 행렬로 5x3x2 + 5x2x6 = 30 + 60 = 90번이다. - A X BC 연산 횟수는
A 행렬 X (BC 행렬 연산 결과) + (BC 행렬 연산)로 5 X 3 X 6 + 3 X 2 X 6 = 90 + 30 = 120번이다.
이때 행렬의 계산 비용을 가장 줄이려면 어떤 순서로 계산해야할까?
위 예시처럼 ABC 행렬에서 AB 행렬과 BC 행렬은 최적 부분 구조 관계를 갖는다. 따라서 각 행렬의 최소 비용과 두 행렬을 곱하는 비용을 더한 값이 답이 된다.

그렇다면 다음 행렬이 주어졌을 때 계산 과정을 알아보자.
- 행렬 A: 5 x 3
- 행렬 B: 3 x 2
- 행렬 C: 2 x 6
- 행렬 D: 6 x 5
각 좌표가 의미하는 바는 다음과 같다.
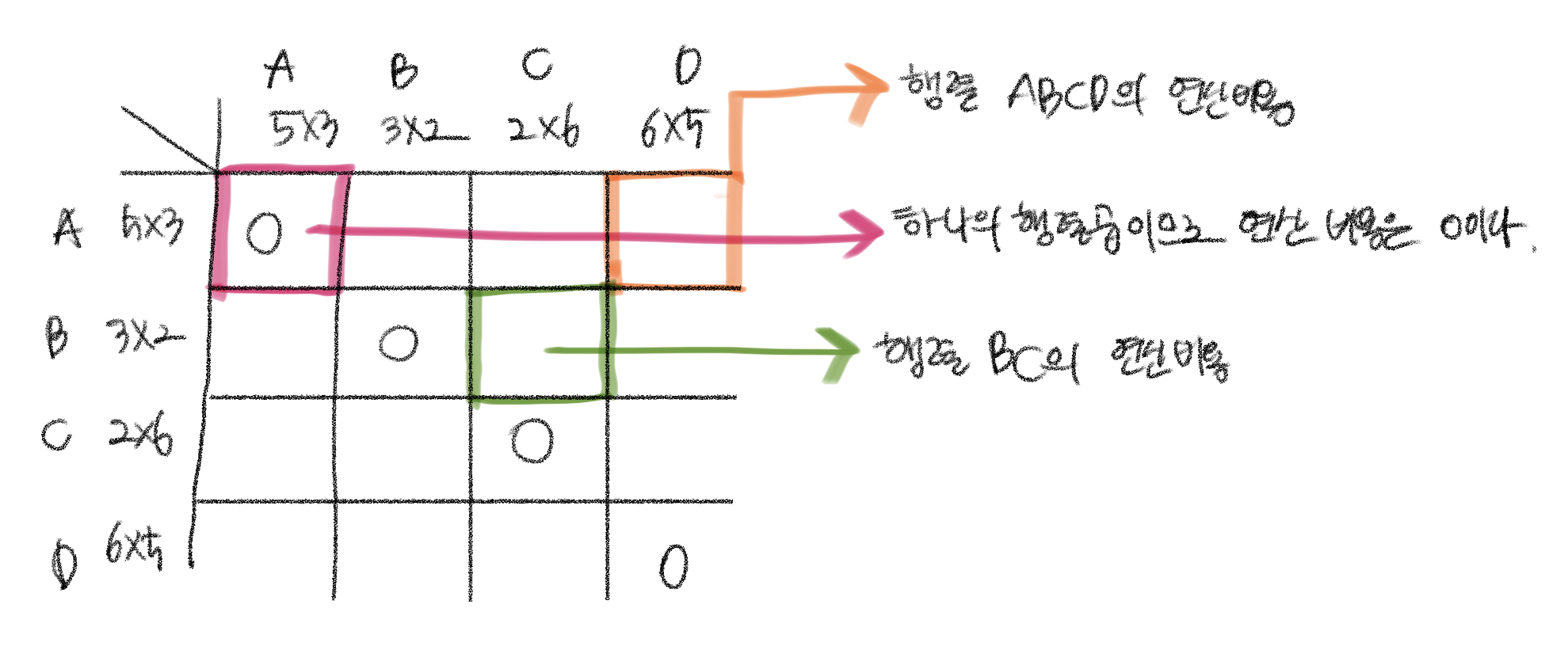
A 행렬과 B 행렬의 연산 횟수를 구한다.(5로 시작하여 2로 끝나는 행렬) 두 행렬 계산 방법은 AB만 존재한다.
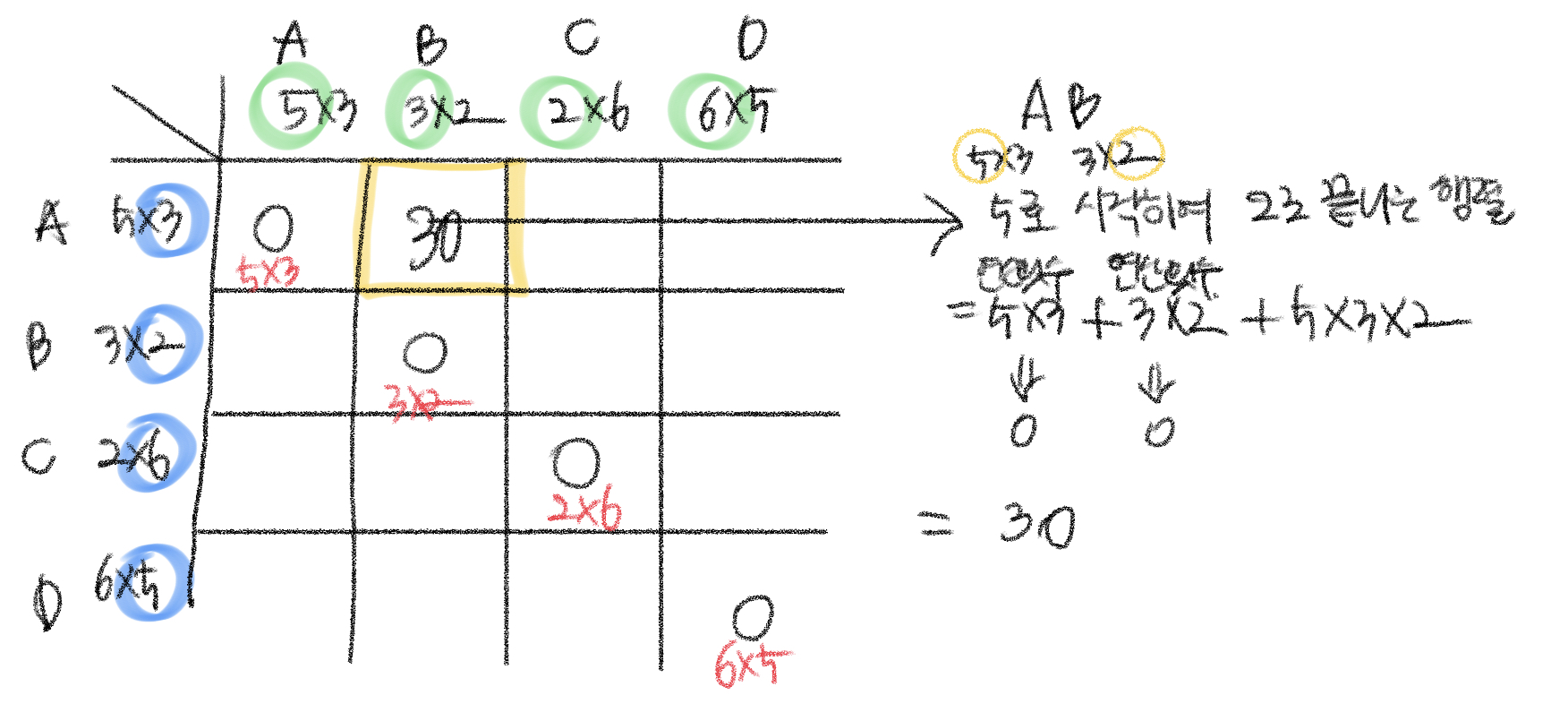
B행렬과 C 행렬의 연산 횟수를 구한다.(3으로 시작하여 6으로 끝나는 행렬) 두 행렬 계산 방법은 BC만 존재한다.
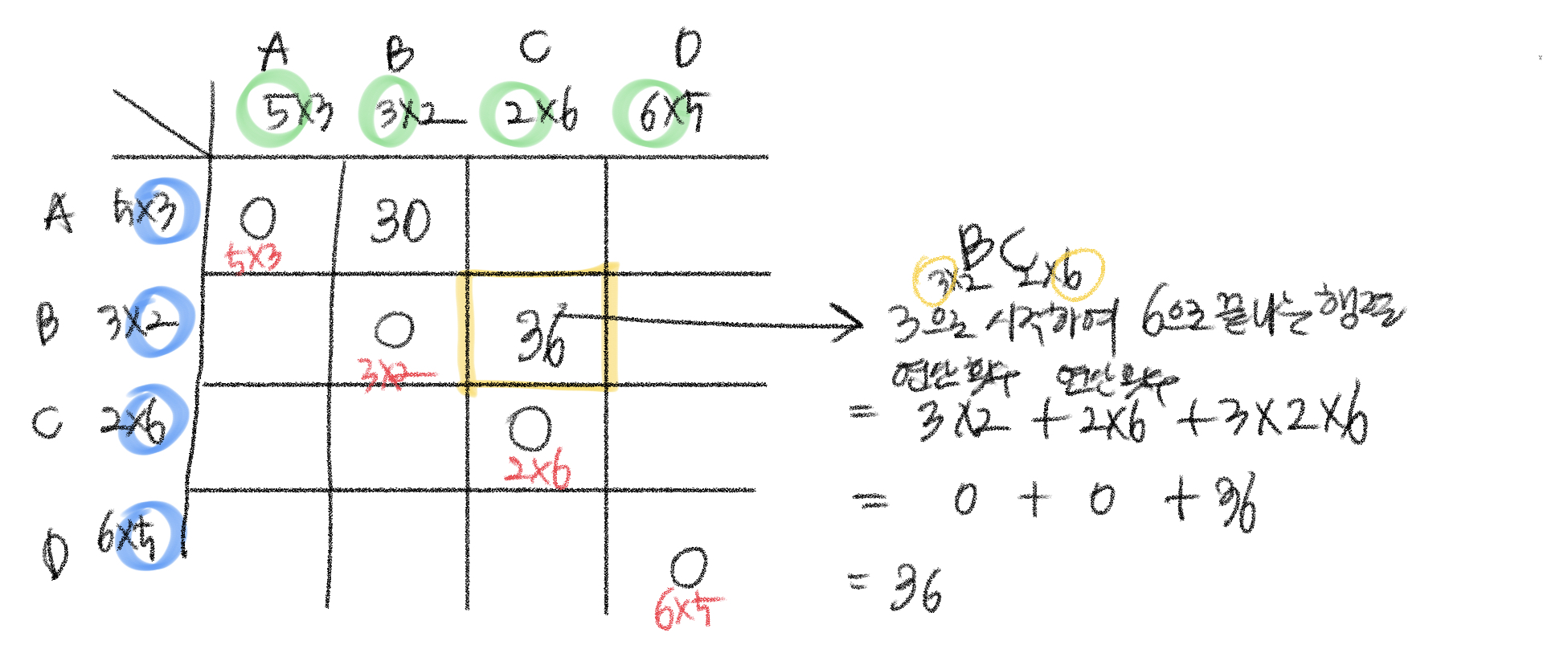
A행렬, B행렬, C행렬의 연산 횟수를 구한다.(5로 시작하여 6으로 끝나는 행렬)
A행렬 X (B행렬 X C행렬), (A행렬 X B행렬) X C행렬을 하는 두 가지 방법이 있다. 이때 더 작은 값을 저장하면 된다.
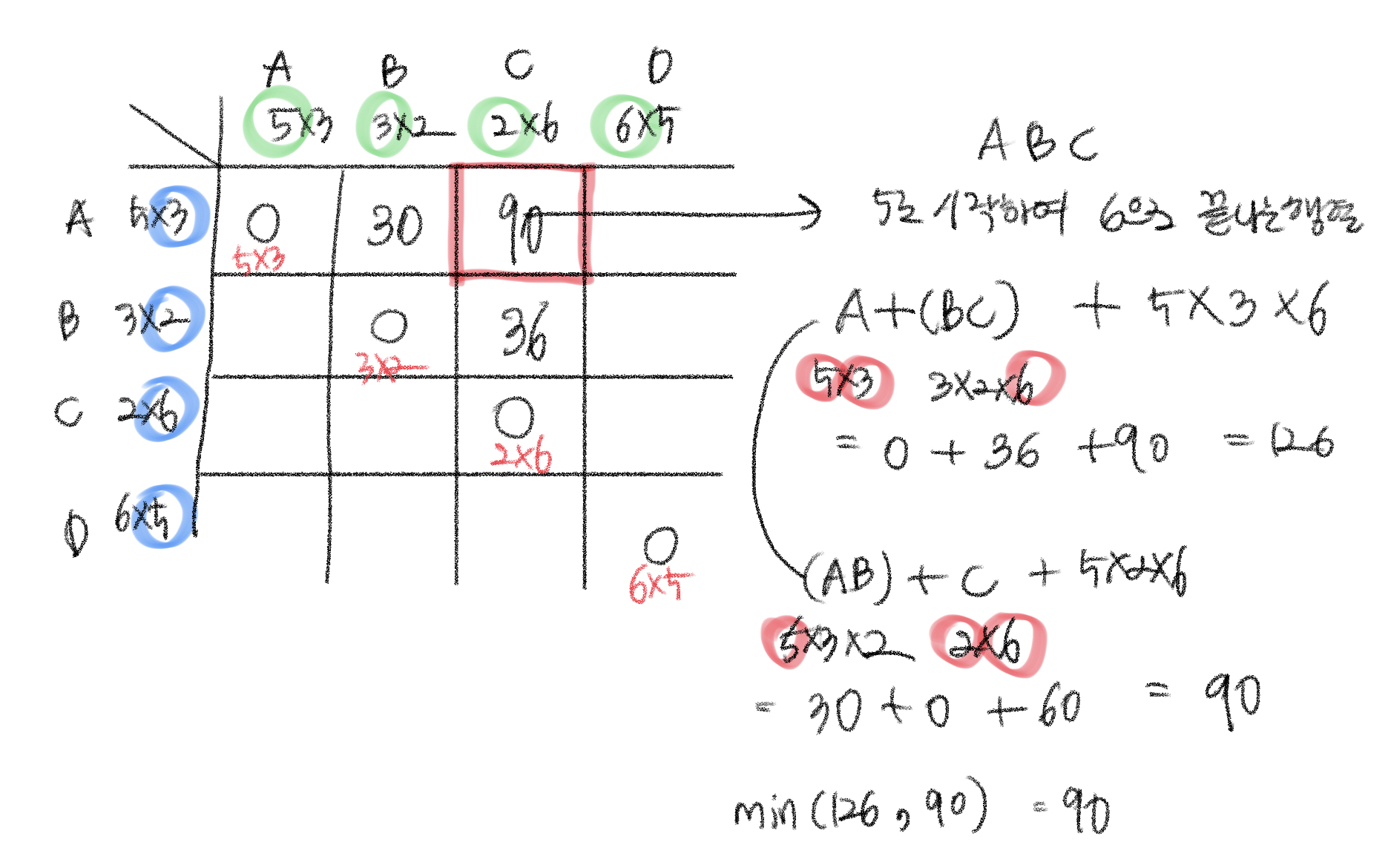
A행렬, B행렬, C행렬, D행렬을 구하는 방법도 다음과 같다.
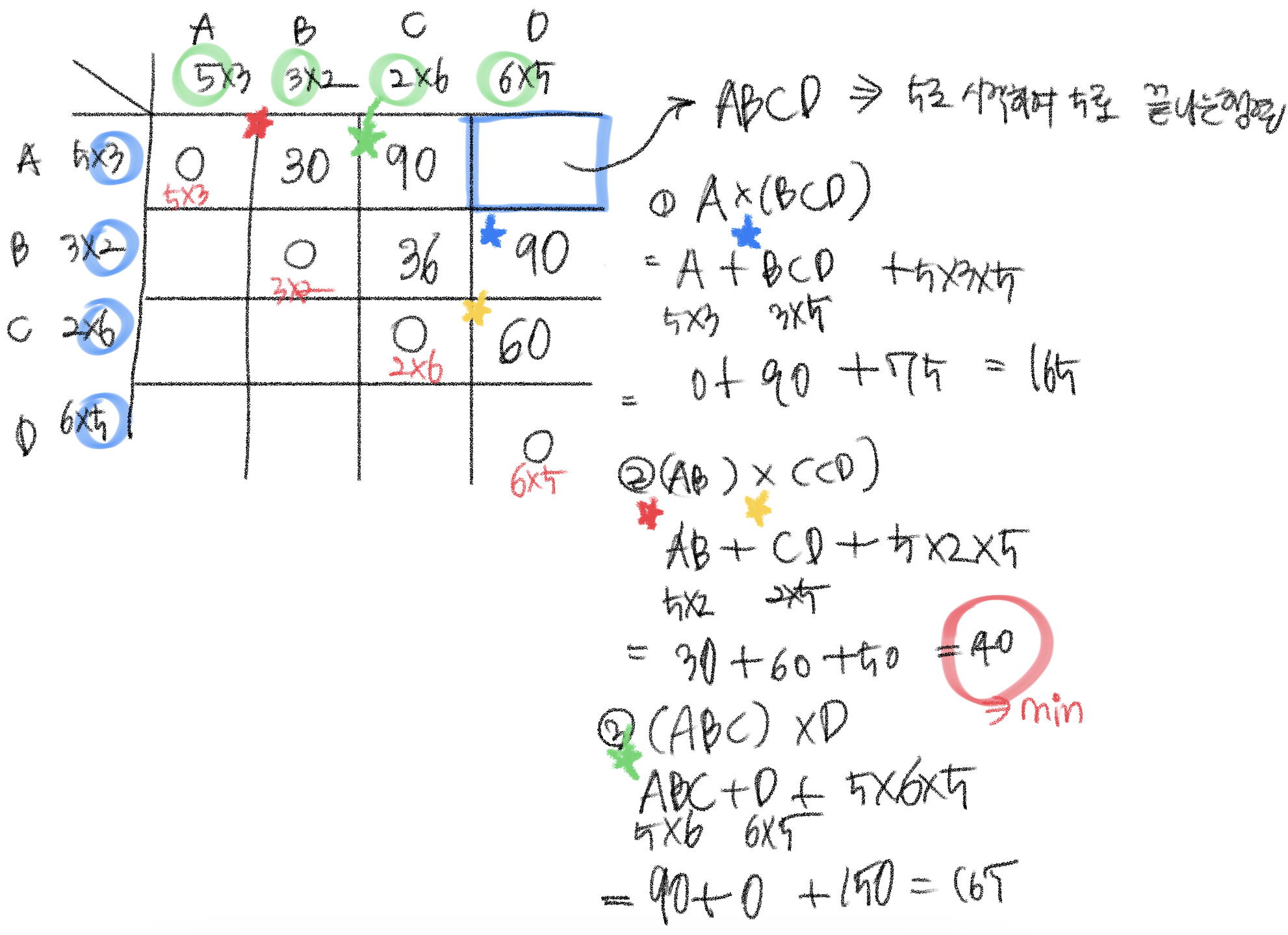
⭐️ 코드
python으로 제출하면 시간초과 발생한다.
from sys import stdin as s
import sys
s = open("input.txt", "rt")
n = int(s.readline())
matrix = [list(map(int, s.readline().split())) for i in range(n)]
dp = [[0] * n for i in range(n)] # 행렬이 하나라면 비용이 0이다.
for cnt in range(n-1):
for i in range(n-1-cnt):
j = i + cnt + 1
dp[i][j] = 2**31 # 가장 큰 수로 업데이트
for k in range(i, j):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + matrix[i][0]*matrix[k][1]*matrix[j][1])
print(dp[0][-1])DP문제는 유형을 파악하는 것과 점화식을 찾는 부분에서 경험이 필요하다고 생각한다. 다양한 문제를 풀이하면서 주어진 시간 안에 적절한 점화식을 찾고 코드로 구현하는 역량을 키워보자.
Reference


잘 보고있어요~