• 코드: https://www.acmicpc.net/problem/2579

설명

계단 오르는 규칙을 살펴보자.

• 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다.
• 연속된 세 개의 계단을 모두 밟을 수 없다.
• 마지막 도착 계단을 반드시 밟아야 한다.

이 규칙을 토대로 4 이상의 하나의 계단을 오를 수 있는 방법은 다음과 같다.

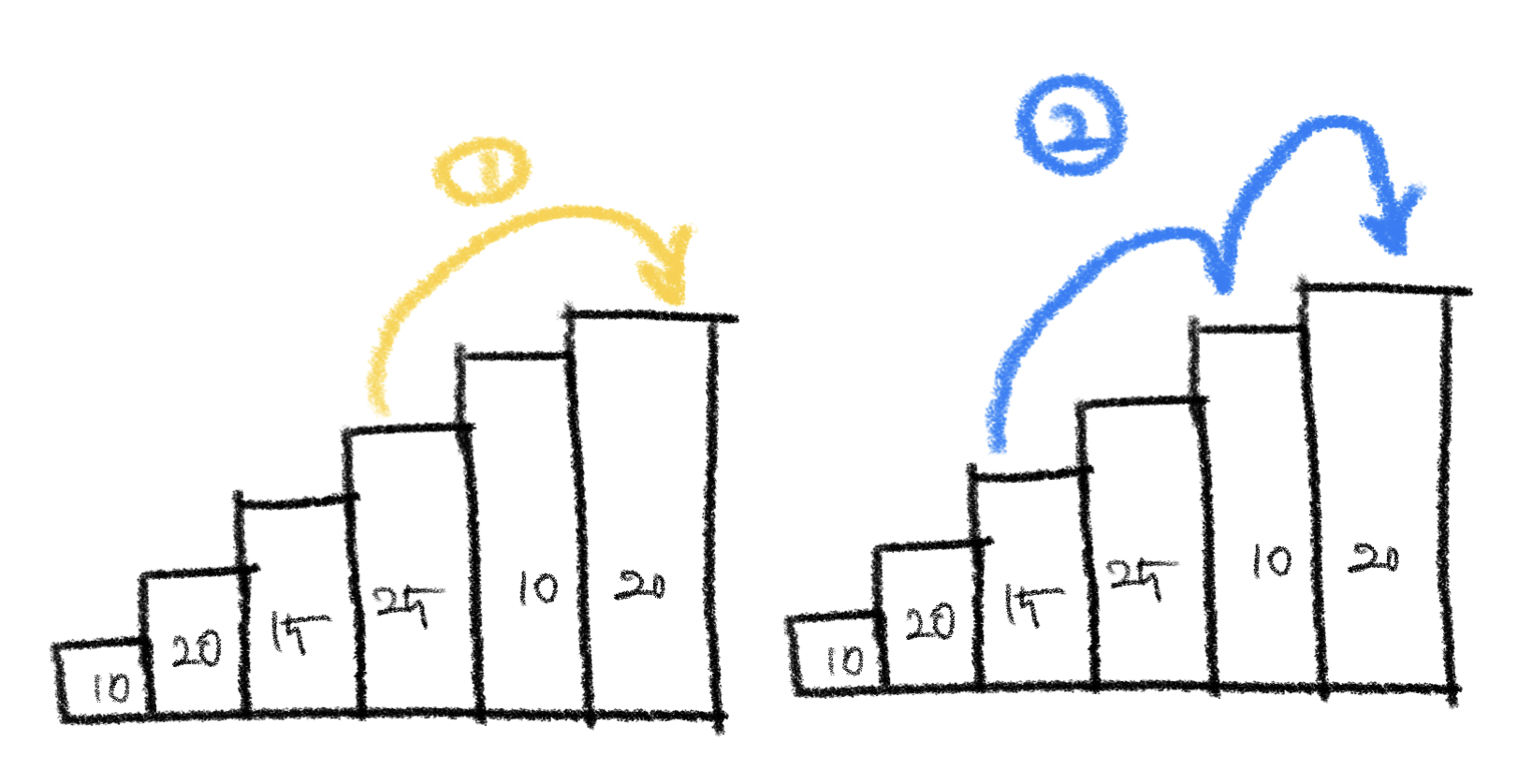
1번은 (n-2)를 밟고 오르는 경우고, 2번은 (n-3)과 (n-1)을 밟고 오른다.
우리는 n번째 칸의 값에 1번과 2번 중 큰 값을 저장하면 되는 것이다.
이를 식으로 표현하면 다음과 같다.
dp[n] = Math.max(dp[n-2], dp[n-3]+stair[n-1]) + stair[n]
2번째에서 dp[n-3]은 n-3까지 계단을 밟는 경우에 가장 큰 값을 의미하고, 그 상태에서 계단 하나를 더 밟는 것이니 계단의 값만 더해주면 된다.
dp 문제는 크게 큰 문제부터 작은 문제로 들어가는 top-down 방식과 작은문제부터 풀어가며 전체 문제를 풀어가는 bottom-up 방식이 있다. bottom-up 방식은 반복문으로 구현된다.

top-down 방식

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class P2579 {
    static int N;
    static Integer[] dp;
    static int[] stairs;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        stairs = new int[N + 1];
        dp = new Integer[N + 1];

        for (int i = 1; i <= N; i++) {
            stairs[i] = Integer.parseInt(br.readLine());
        }

        dp[0] = stairs[0];
        dp[1] = stairs[1];

        if (N >= 2) {
            dp[2] = stairs[1] + stairs[2];
        }

        System.out.println(find(N));
    }

    private static int find(int n) {
        if (dp[n] == null) {
            dp[n] = Math.max(find(n - 2), find(n - 3) + stairs[n - 1]) + stairs[n];
        }
        return dp[n];
    }
}

bottom-up 방식

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class P2579 {
    static int N;
    static Integer[] dp;
    static int[] stairs;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        stairs = new int[N + 1];
        dp = new Integer[N + 1];

        for (int i = 1; i <= N; i++) {
            stairs[i] = Integer.parseInt(br.readLine());
        }

        dp[0] = stairs[0];
        dp[1] = stairs[1];

        if (N >= 2) {
            dp[2] = stairs[1] + stairs[2];
        }

		for(int i = 3; i <= N; i++) {
        	dp[i] = Math.max(dp[i-2], dp[i-3] + stairs[i-1]) + stairs[i];
        }
        System.out.println(dp(N));
    }
}

Reference

• https://girawhale.tistory.com/3
• https://st-lab.tistory.com/132