• 문제 링크: https://www.acmicpc.net/problem/9465

돌던지기 문제를 이해하기 위해 풀어봤다.

설명

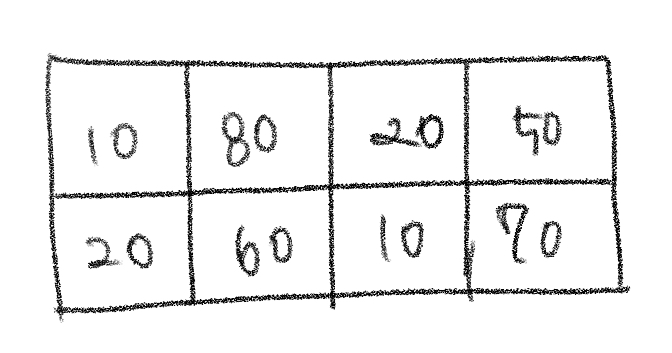
• 뗄 수 있는 스티커 점수의 최댓값을 구한다.
• 한 스티커를 떼면 주변에 붙어있는 스티커(상, 하, 좌, 우)는 뗄 수 없다.

DP를 이용하여 풀이한다.

n이 5인 스티커가 있다.

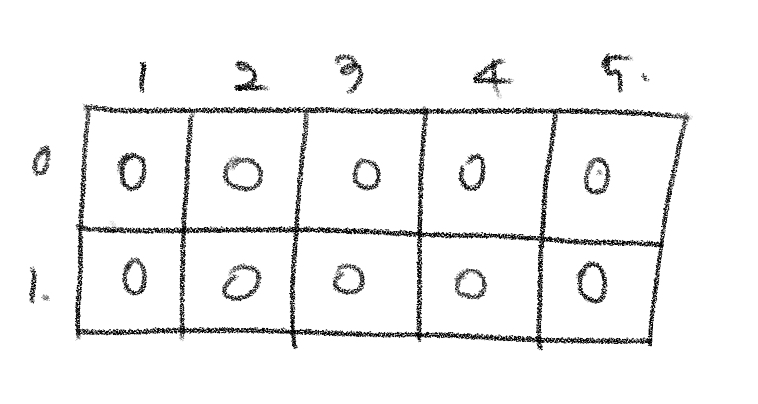
(0,1) 위치의 스티커를 뗀다면 (0,2), (1,1)은 사용할 수 없다.

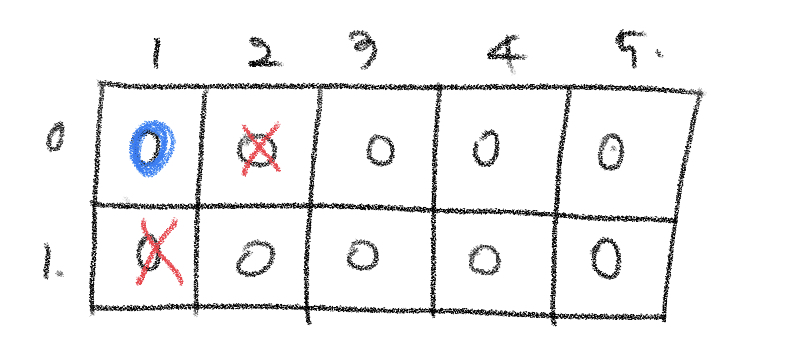
(1,2) 위치의 스티커를 뗀다. 이 경우 1번과 2번 세로줄만 생각했을 때, 가장 스티커의 합이 커지는 경우는 (0,1)과 (1,2)에 있는 스티커를 뗀 경우이다.

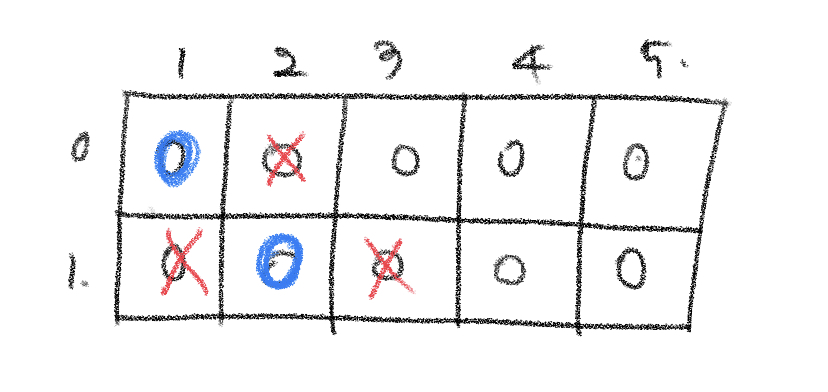
(0,3) 위치의 스티커를 뗀 경우의 수는, 다음과 같다.

즉 (0,3) 기준으로 직전에 있는 왼쪽 대각선 아래, 왼쪽 대각선 아래의 왼쪽을 확인했을 때 더 큰 값을 현재 위치에 넣어준다.

• DP를 고려하면, dp[1][2]에는 (0,1)과 (1,2) 위치의 합을 저장하고 있다.

이렇게 배열의 끝까지 가서, 더 큰 값을 결과값으로 반환한다.

코드

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int T, N;
    static int[][] sticker;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        T = Integer.parseInt(st.nextToken());

        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine());
            N = Integer.parseInt(st.nextToken());
            // 세로 0번째 인덱스는 0으로 두고 1부터 N까지 사용한다.
            sticker = new int[2][N + 1];
            // dp에서 더해나갈 dp 배열
            int[][] dp = new int[2][N + 1];

            // initialize
            for (int j = 0; j < 2; j++) {
                String[] inputs = br.readLine().split(" ");
                for (int k = 1; k <= N; k++) {
                    sticker[j][k] = Integer.parseInt(inputs[k - 1]);
                }
            }

            // 첫번째 column은 앞에 숫자가 없으므로 스티커 배열이 된다.
            dp[0][1] = sticker[0][1];
            dp[1][1] = sticker[1][1];

            for (int j = 2; j <= N; j++) {
                dp[0][j] = Math.max(dp[1][j - 1], dp[1][j - 2]) + sticker[0][j];
                dp[1][j] = Math.max(dp[0][j - 1], dp[0][j - 2]) + sticker[1][j];
            }
            // 맨 마지막 줄에서 더 큰 dp를 갖는 것을 출력한다.
            System.out.println(Math.max(dp[0][N], dp[1][N]));
        }
    }
}

Reference

• https://velog.io/@yanghl98/%EB%B0%B1%EC%A4%80-9465-%EC%8A%A4%ED%8B%B0%EC%BB%A4-JAVA