BOJ - 1504

백준 문제 링크
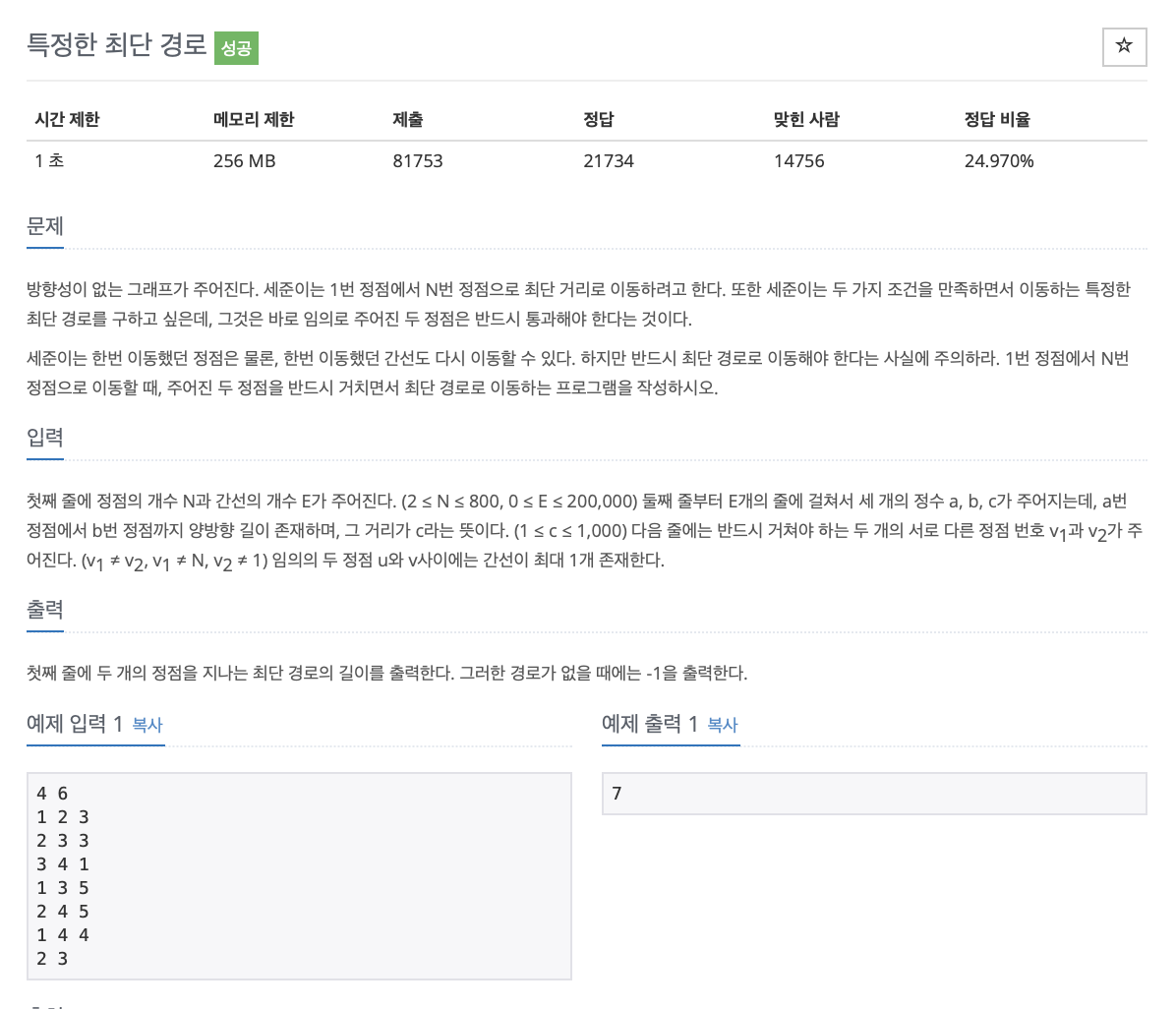
특정한 최단 경로

❓접근법

1. 다익스트라 알고리즘을 사용했다.
2. 문제에서 나온 정점과 간선을 모두 다 graph에 넣어준다.
3. 다익스트라 함수 find_way를 만들어
   distance를 정의하고, 마지막엔 distance를 반환한다.
4. 우리가 구하고자 하는 것은,

• 1번 -> v1 -> v2 -> n 혹은 1 -> v2 -> v1 -> n 중 최단 거리
  • [1 -> v1, v1 -> v2, v2 -> n] 3개의 변수
  • [1 -> v2, v2 -> v1, v1 -> n] 3개의 변수
    총 6개의 변수를 만들어서, 그 중 작은 값을 answer로 지정한다.

5. 만약 answer >= INF이면 -1을, 아니면 answer를 출력하면 끝!

👌🏻코드

import heapq

INF = int(1e9)

n, e = map(int, input().split())

graph = [[] for _ in range(n + 1)]


for _ in range(e):
    
    a, b, c = map(int, input().split())
    graph[a].append((b, c))
    graph[b].append((a, c))
    

def find_way(start):
    
    distance = [INF] * (n + 1)
    
    q = []
    
    heapq.heappush(q, (0, start))
    distance[start] = 0
    
    while q:
        
        dist, now = heapq.heappop(q)
        
        if distance[now] < dist:
            continue
            
        for i in graph[now]:
            
            cost = dist + i[1]
            
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))
                
    return distance

v1, v2 = map(int, input().split())

# 1 ~ v1 까지 가는 방법
a_1 = find_way(1)[v1]

# v1 ~ v2 까지 가는 방법
b_1 = find_way(v1)[v2]

# v2 ~ n 까지 가는 방법
c_1 = find_way(v2)[n]


# 1 ~ v2 까지 가는 방법
a_2 = find_way(1)[v2]

# v2 ~ v1 까지 가는 방법
b_2 = find_way(v2)[v1]

# v1 ~ n 까지 가는 방법
c_2 = find_way(v1)[n]

answer = min((a_1 + b_1 + c_1), (a_2 + b_2 + c_2))

if answer >= INF:
    print(-1)
else:
    print(answer)