BOJ - 1613

백준 문제 링크
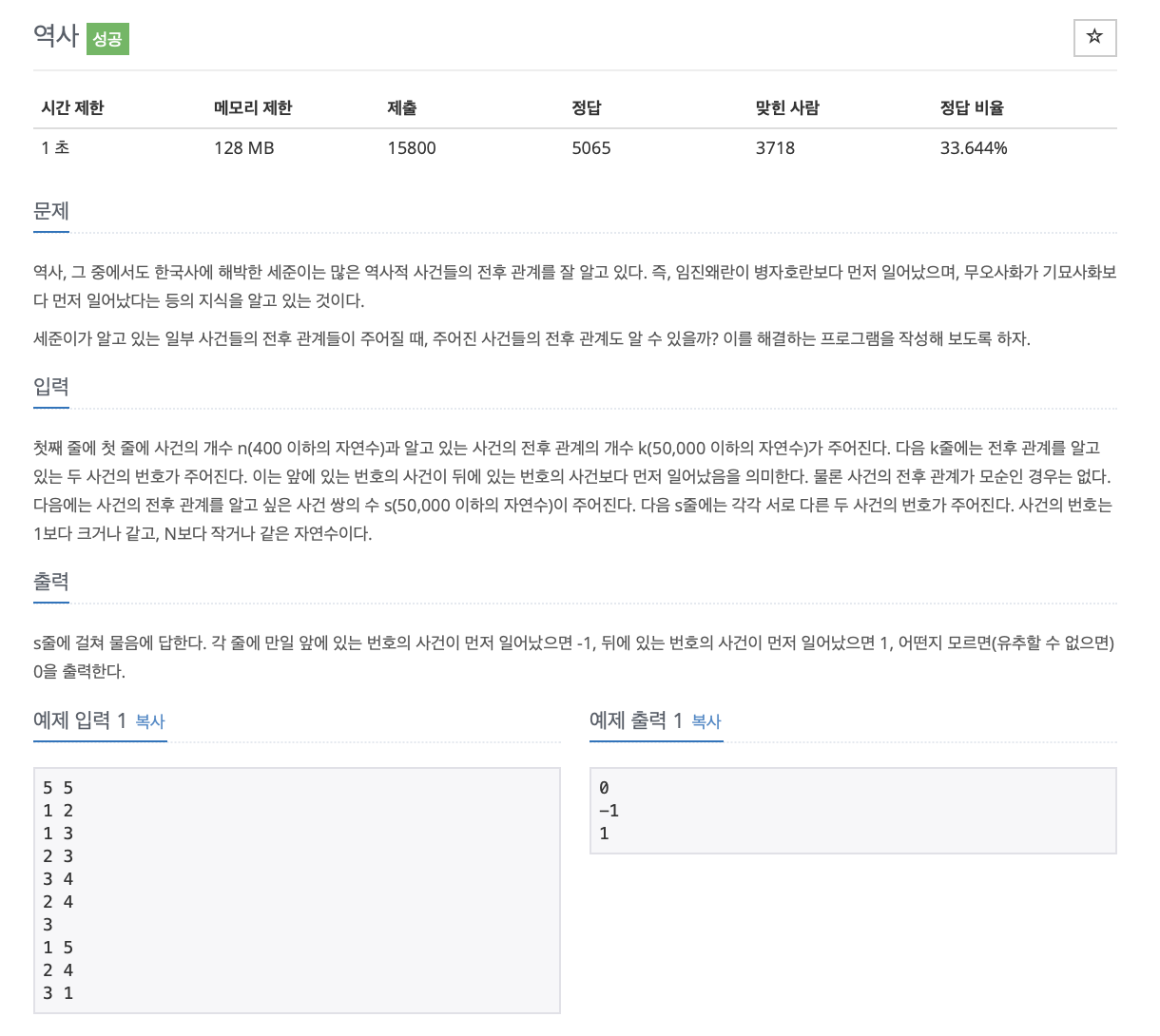
역사

❓접근법

1. 플로이드 워셜 알고리즘을 활용했다.
2. INF로 이루어진 2차원 리스트 graph를 만들고,
   자기 자신은 0으로, 전 후 관계를 아는 번호는 1로 지정한다.
3. 3중 반복문으로 최단 거리 테이블을 갱신한다.
4. 앞의 번호(a), 뒤의 번호(b)를 받은 후 조건을 적용한다.

• graph[a][b] 와 graph[b][a] 둘 다 INF이면 0을 출력
• 둘 중 하나라도 INF가 아닐 때
  • graph[a][b] < graph[b][a] 이면 앞이 더 빠르므로 -1 출력
  • graph[a][b] > graph[b][a] 이면 뒤가 더 빠르므로 1 출력

👌🏻코드

n, k = map(int, input().split())

INF = int(1e9)

graph = [[INF] * (n + 1) for _ in range(n + 1)]

for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0
            
for _ in range(k):
    a, b = map(int, input().split())
    
    graph[a][b] = 1
    
    
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
    
    
s = int(input())
for _ in range(s):
    a, b = map(int, input().split())
    
    if graph[a][b] == INF and graph[b][a] == INF:
        print(0)
        
    else:
        if graph[a][b] < graph[b][a]:
            print(-1)
        else:
            print(1)

❌틀린 코드

import heapq

n, k = map(int, input().split())

INF = int(1e9)

graph = [[] for _ in range(n + 1)]

for _ in range(k):
    a, b = map(int, input().split())
    graph[a].append((b, 1))
   
def dijkstra(start):
    
    distance = [INF] * (n + 1)    
    
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0
    
    while q:
        dist, now = heapq.heappop(q)
        
        if distance[now] < dist:
            continue
            
        for i in graph[now]:
            
            cost = dist + i[1]
            
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost , i[0]))
                
    return distance

s = int(input())

for _ in range(s):
    x, y = map(int, input().split())
    
    if dijkstra(x)[y] == INF and dijkstra(y)[x] == INF:
        print(0)
        
	elif dijkstra(x)[y] != INF or dijkstra(y)[x] != INF:
        if dijkstra(x)[y] < dijkstra(y)[x]:
            print(-1)
        else:
            print(1)

처음엔 다익스트라 알고리즘을 활용했는데, 시간 초과가 났다 ;;;;;