ML_Regularization

wnsdnl·2025년 3월 8일

ML 머신러닝

목록 보기

6/11

📌 편향(Bias)과 분산(Variance)

📍 편향(Bias)

편향이란 추정 결과 한 쪽으로 치우치는 경향을 보임으로써 발생하는 오차이다. 머신러닝 모델 측면에서의 편향은 예측값과 정답값의 차이를 말한다. 따라서 편향이 클수록 예측과 정답 간 차이가 크다고 할 수 있다.

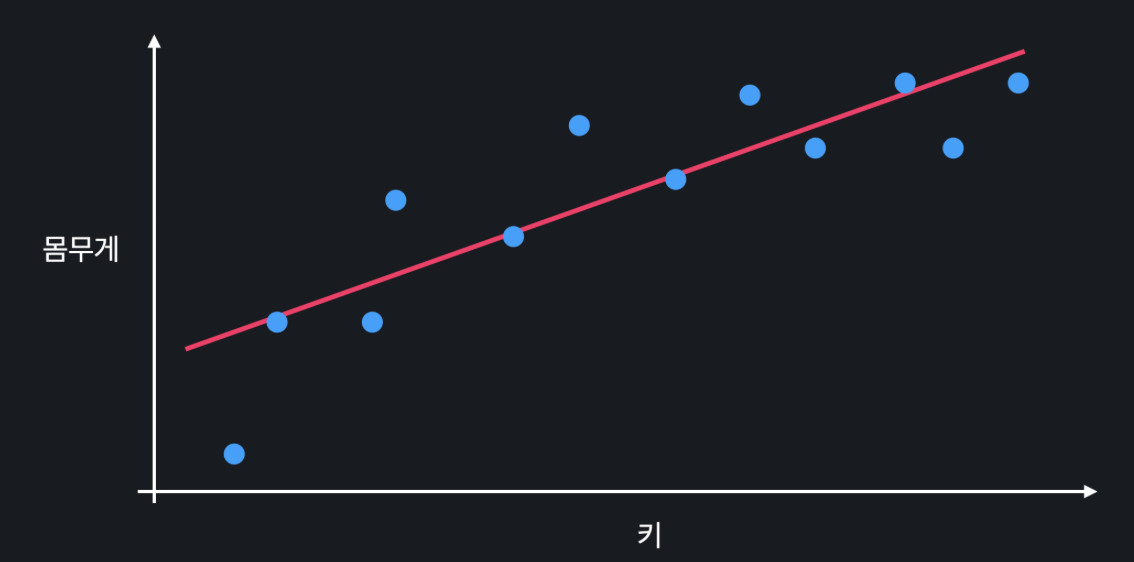
사람의 키를 이용해서 몸무게를 예측하고 싶다고 할 때, 위의 직선은 키와 몸무게의 관계를 잘 표현하고 있는 거 같지 않다. 오히려 곡선으로 나타낼 때 더 잘 표현할 수 있을 거 같다.
이렇게 모델이 너무 간단해서 데이터의 관계를 잘 학습하지 못하는 경우, 모델의 편향이 높다고 할 수 있는 것이다.

편향이 작은 경우는 어떨까?

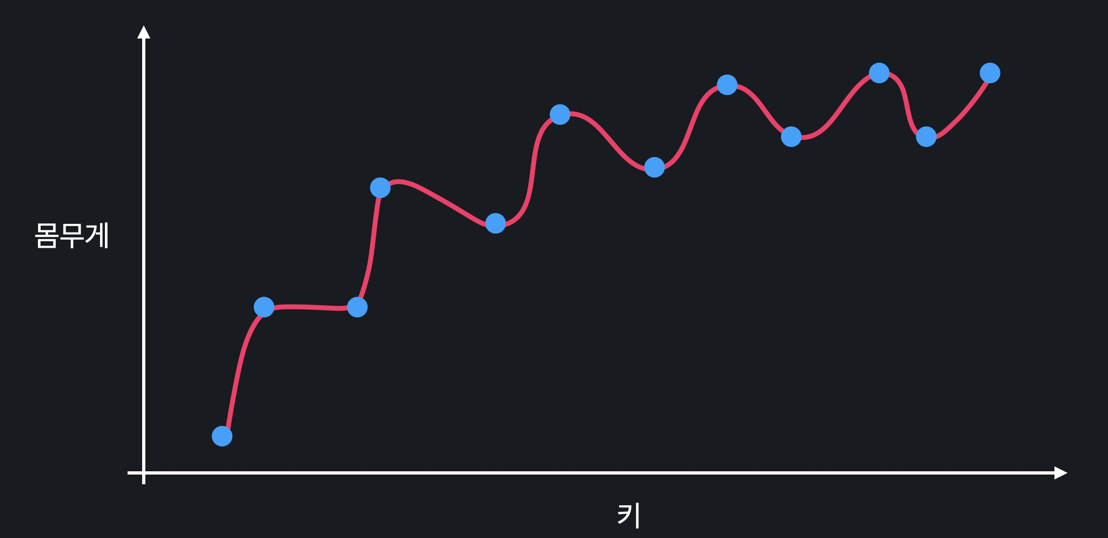
높은 차항의 회귀를 사용해서, 위와 같은 관계를 학습했다고 하자. 이 복잡한 곡선은 training 데이터에 거의 완벽히 맞춰져 있기 때문에 훈련 데이터셋의 예측과 정답간의 오차가 적다. 따라서 이 모델은 편향이 낮은 모델이라 할 수 있다.

📍 분산(Variance)

머신러닝 모델 측면에서 분산이란, 모델이 여러 데이터셋에 대해서 얼만큼 flexibility를 가지는지를 말한다. 분산의 본래 의미와 같이 얼만큼 예측값이 퍼져서 다양하게 출력될 수 있는 정도로 해석한다. (예측값의 변동성)

따라서 다양한 데이터 셋 간에 성능 차이가 많이 나면 분산이 높다고 하고, 성능이 비슷하면 분산이 낮다고 한다.

위에서 봤던 단순한 직선 모델과 복잡한 곡선 모델을 이용해서 처음 보는 test 데이터의 몸무게를 예측해 본다고 하자.

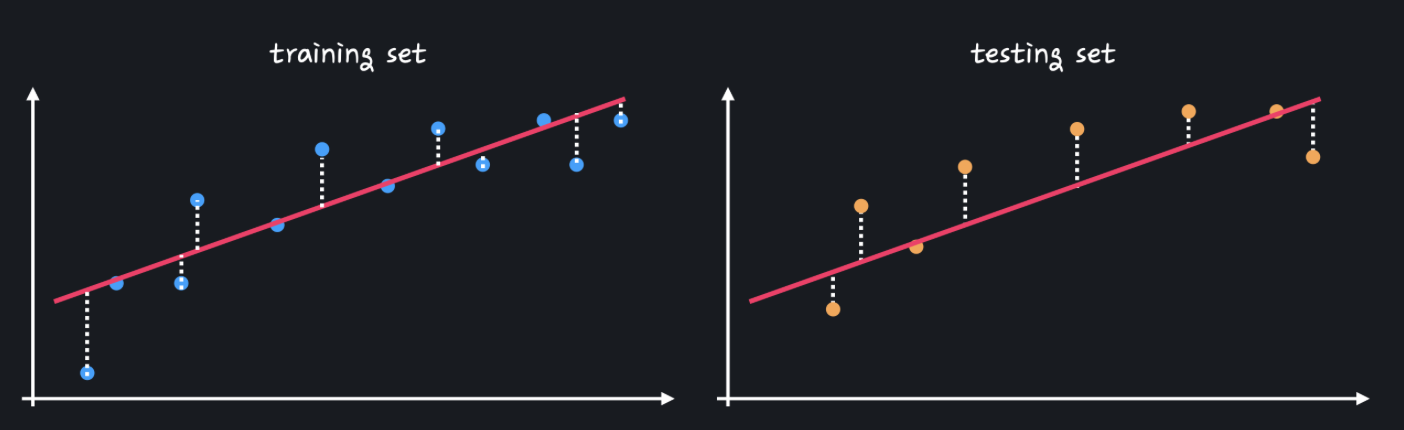
위의 사진을 보면 training set을 사용했을 때와 test set을 사용했을 때 성능에 큰 차이가 없다. 이는 다양한 데이터 셋을 사용해도 일관된 성능을 보인다는 것이므로 직선 모델은 분산이 작다. (데이터셋들에 대한 예측값의 변동폭이 작다 = 분산이 작다)

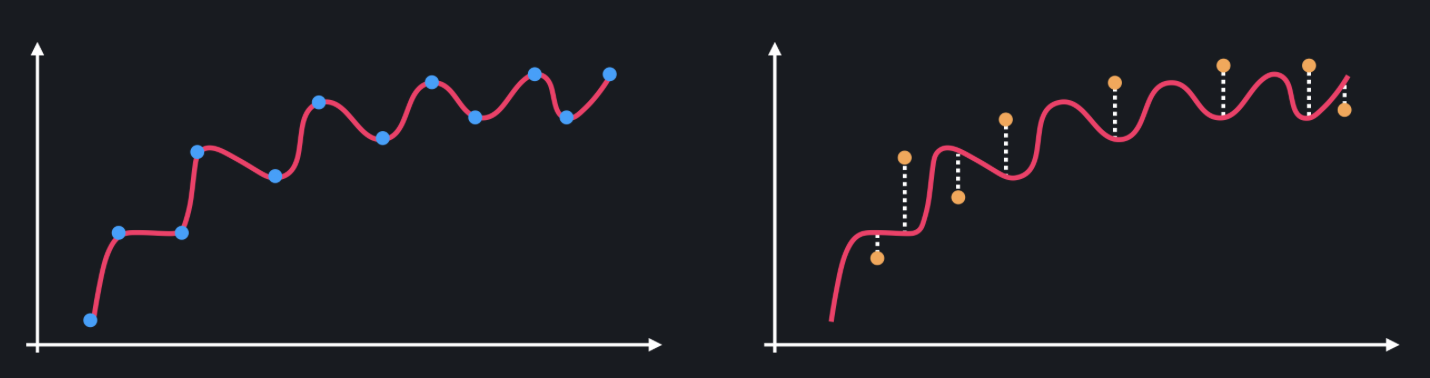
그에 비해 곡선 모델은 training 데이터에 대해서는 거의 완벽한 성능을 보이지만 test 데이터에 대해서는 상당히 안 좋은 성능을 보인다.
모델이 training 데이터를 가지고 학습할 때 키와 몸무게의 관계를 배우기보다는 아예 데이터 자체를 외워버리기 때문에 처음 보는 test 데이터 셋에 모델을 적용해 보면 성능이 아주 떨어지는 거다. 즉, 새로운 데이터에 대한 일반화 성능이 떨어진다.
따라서 복잡한 곡선 모델은 예측의 변동폭이 상당히 크기 때문에 분산이 크다고 볼 수 있다. (데이터셋이 바뀔 때마다 모델의 예측값의 변화가 크다. = 분산이 크다)

정리하자면 다음과 같다.

편향
- 편향이 높다: 주어진 데이터의 관계를 잘 학습하지 못한다
- 편향이 낮다: 주어진 데이터의 관계를 아주 잘 학습한다.

분산
- 분산이 높다: 데이터 셋에 따라 성능의 편차가 크다.
- 분산이 낮다: 어떤 데이터 셋에 적용해도 성능이 비슷하게 나온다.

📍 Bias-Variance Trade off

편향이 크고 분산이 작으면 모델이 데이터에 Underfit(과소적합) 되었다고 한다.

편향이 작고 분산이 크면 모델이 데이터에 Overfit(과적합) 되었다고 한다.

따라서 모델이 training 데이터의 관계를 잘 나타내지 못하면 과소적합, 관계를 지나치게 잘 나타내면 과적합이 된다.

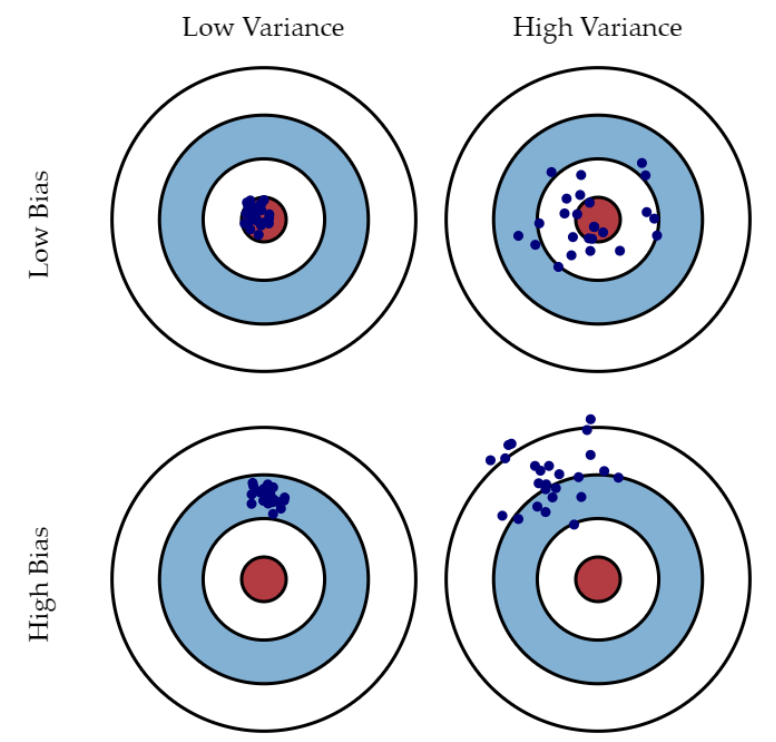
알다시피 편향과 분산은 trade-off 관계에 있기 때문에 하나가 줄어들수록 다른 하나는 늘어난다. 따라서 이 둘 사이의 적당한 관계를 찾아내는 것이 중요하다. 그래프로 표현하면 아래와 같다.

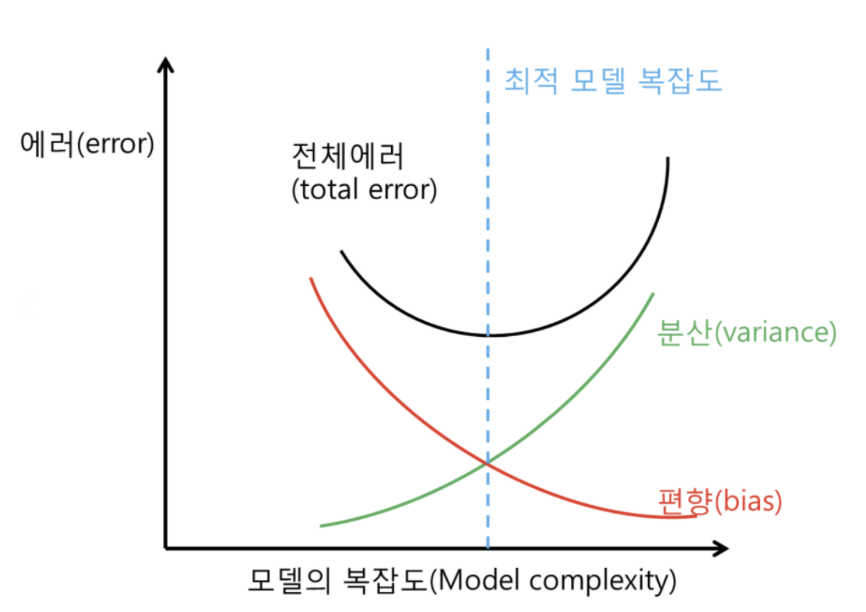
모델의 복잡도가 증가할 수록 분산은 커지고, 편향은 작아진다. 전체 에러는 초반에 감소하다가 분산이 커지고 과적합이 되기 시작하면서 다시 증가한다.
따라서 전체 에러가 증가하기 직전까지가 모델의 최적 복잡도라 할 수 있다.

봤다시피 모델의 복잡도가 증가할 수록 과적합이 되어서 성능이 안 좋아지는데, Big-data(데이터 수가 많음)가 전제된다면 성능이 유지될 수는 있다.

Big-data가 전제되면 훈련 데이터가 모집단과 거의 유사하다. 이는 여러 데이터셋을 sampling 해도 모두 비슷한 결과가 나올 수 있기 때문에 모델의 복잡도를 높여도 전체 에러가 증가하지 않는 것이다. 이는 많은 양의 데이터를 학습하는 딥러닝에서 자주 일어날 수 있는 일이다.

그럼 Big-data가 전제되지 않을 때, 모델의 복잡도는 올리면서 과적합을 방지할 수 있는 방법은 없을까?

그 방법 중 하나인 Regularization 즉, 정규화에 대해서 알아보자.

📌 Regularization (정규화)

‘정규화’라는 기법은 학습 과정에서 모델이 과적합 되는 것을 예방한다.

예를 들어 다음과 같은 과적합이 된 모델이 있다고 하자.

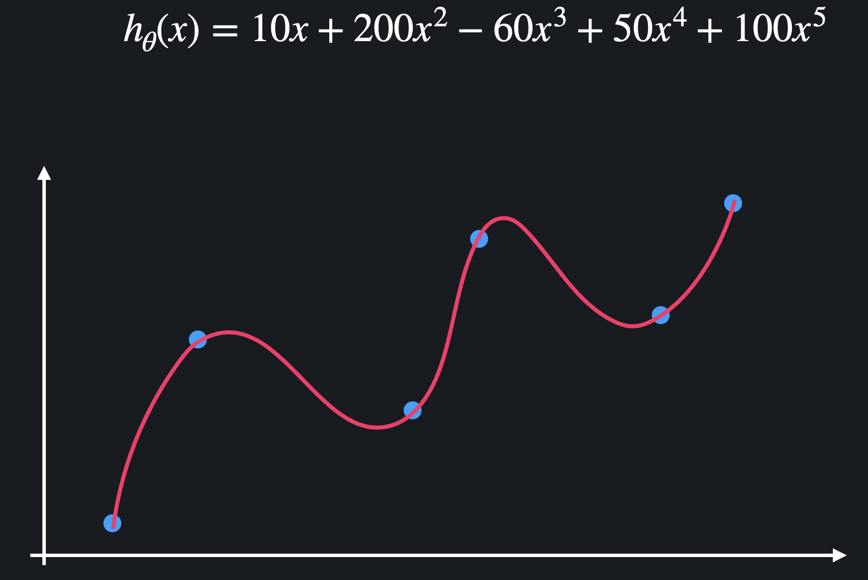
과적합된 함수는 보통 위아래로 엄청 왔다 갔다 한다는 특징이 있다. 많은 굴곡을 이용해서 함수가 training 데이터를 최대한 많이 통과하도록 하는 것이다.
함수가 이렇게 급격하게 변화한다는 건 함수의 계수, 즉 가설 함수의 $\theta$ 값들이 굉장히 크다는 뜻이다. (그래프가 휘게 되려면 높은 계수가 필요)

따라서 정규화는 모델을 학습시킬 때 $\theta$ 값들이 너무 커지는 것을 방지해준다. $\theta$ 값들이 너무 커지는 걸 방지하면 training 데이터에 대한 오차는 조금 커질 수 있어도, 위아래로 변동이 엄청 심하던 가설 함수를 좀 더 완만하게 만들 수 있다. 그 결과는 아래와 같다.

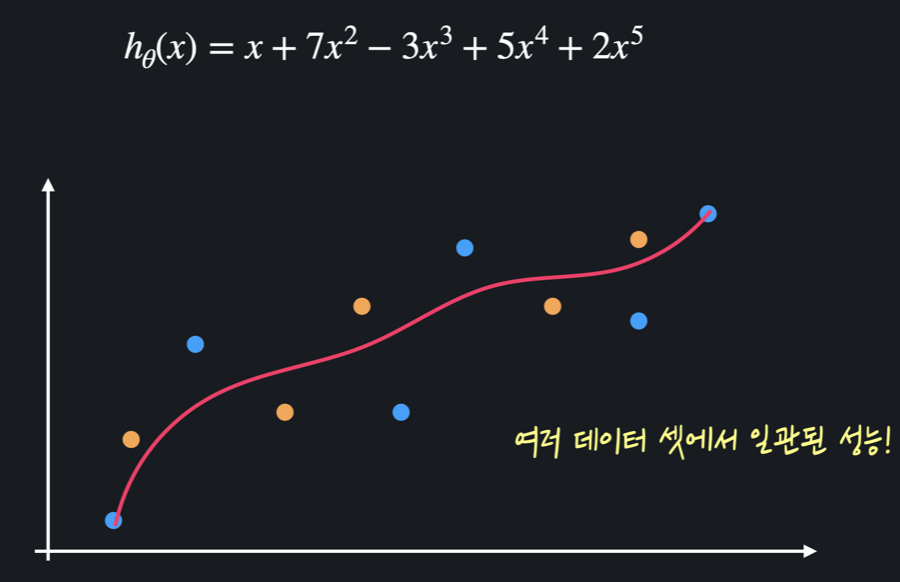
정규화를 하면 정규화를 하기 전보다 여러 데이터 셋에 대해 더 일관된 성능을 보이기 때문에 과적합을 막을 수 있다.

정규화를 하는 기법에는 L1 정규화와 L2 정규화가 있다.

📍 L1 Regularization

우리가 봐왔던 손실 함수는 다음과 같다.

J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2

이때는 손실 함수의 아웃풋이 작을수록 더 좋은 가설 함수고, 손실 함수의 아웃풋이 클수록 더 안 좋은 가설 함수라고 했었다. 따라서 훈련 데이터셋에 대한 평균 제곱 오차가 작을 수록 손실 함수의 아웃풋도 더 작으므로 좋게 평가했다.

하지만 과적합을 배우고 난 후에는 어떤가? 훈련 데이터셋에 대해서 오차가 0에 가까울 만큼 작다고 해서 그 모델이 무조건적으로 성능이 좋은 건 아니었다. 모델의 복잡도가 올라가 $\theta$ 가 굉장히 커져버려 훈련 데이터에 과적합되었을 수도 있기 때문이다. 이러면 알다시피 새로운 데이터들에 대해서는 일반화 능력이 떨어지기에 성능은 안 좋은 것이다.

따라서 이제부턴 좋은 가설 함수의 기준을 조금 바꿔준다. training 데이터에 대한 오차도 작고 $\theta$ 값들도 작아야 좋은 가설 함수다. $\theta$ 가 크면 함수가 많이 휘게 되면서 훈련 데이터셋에 과적합이 될 가능성이 크기 때문에 $\theta$ 값들도 작아야 한다는 기준을 추가한 것이다.

그래서 손실 함수에 다음과 같은 정규항을 추가한다.

\lambda\sum_{i=1}^{n}|\theta_i|

L1 Regularization의 정규항은 $\theta$ 값들의 절댓값을 모두 더해준다. ( $\theta_0$ 은 과적합과 상관이 없기 때문에 $\theta_0$ 의 절댓값은 더해주지 않는다.)

여기서 $\lambda$ 는 $\theta$ 값들이 커지는 것에 대해서 얼마나 많은 페널티를 줄 건지를 정해주는 역할을 한다. 예를 들어 $\lambda$ 가 100이면 $\theta$ 값들이 조금만 커져도 손실 함수가 굉장히 커지는 반면, $\lambda$ 가 0.01이면 $\theta$ 값들이 커져도 손실 함수는 별로 안 커지기 때문에 평균 제곱 오차를 줄이는 게 중요한 문제가 된다.
따라서 $\lambda$ 는 데이터에 대한 오차 줄이기와 $\theta$ 값 줄이기 중 어떤 것을 더 중요하게 볼지를 $\lambda$ 로 결정시킬 수 있다. $\lambda$ 가 클수록 $\theta$ 값을 줄이는 게 더 중요하고 $\lambda$ 가 작을 수록 데이터의 오차를 줄이는 게 더 중요해진다.

손실 함수와 정규항을 결합시킨 식은 아래와 같다.

J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{i=1}^{n}|\theta_i|

L1 정규화를 사용하는 모델을 Rasso 회귀 모델, 줄여서는 Rasso 모델이라고 한다.

📍 L2 Regularization

L2 정규화는 L1 정규화와 같은 개념이지만 정규항에서 차이가 있다. L2 정규화의 정규항은 다음과 같다.

\lambda\sum_{i=1}^{n}\theta_i^2

L2 정규화는 $\theta$ 의 절댓값이 아닌 제곱값을 더해주는 것이다. L1 정규화와 마찬가지로 $\theta$ 값이 크면 손실이 커지기 때문에 $\theta$ 값들이 커지는 것을 방지해준다. 손실 함수와 결합시킨 식은 아래와 같다.

J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{i=1}^{n}\theta_i^2

이렇게 L2 정규화를 사용하는 회귀 모델을 Ridge 회귀 모델, 줄여서 Ridge 모델이라고 한다.

정리하자면 L1, L2 정규화는 손실 함수의 두 항(데이터의 오차, $\theta$ 값들의 절댓값 혹은 제곱합)을 모두 줄이는 방향으로 가설 함수를 찾게 된다. 그리고 둘 중에 무엇을 더 중요하게 볼지는 $\lambda$ 로 결정한다.

💡 구현

sklearn으로 한 번 L1, L2 정규화를 구현해보자.
일단 L1 정규화는 Lasso 모델을 불러와서 사용하면 끝이다.

from sklearn.linear_model import Lasso

model = Lasso(alpha=0.1, max_iter=1000)

alpha값은 $\lambda$ 를 의미한다. max_iter 는 최대 몇 번 반복할지를 나타낸다.

L2 정규화는 여기서 Ridge 모델을 불러와 똑같이 진행하면 된다.

from sklearn.linear_model import Ridge

model = Ridge(alpha=0.1, max_iter=1000)

📍 정규화 일반화

정규화는 모델의 파라미터(즉 학습을 통해 찾고자 하는 값들 - 회귀의 경우 $\theta$ )에 대한 손실 함수를 최소화 하는 모든 알고리즘에 적용할 수 있다. 따라서 다중 회귀, (다중) 다항 회귀, 로지스틱 회귀 모델 모두 정규화를 적용할 수 있다. 방법은 그냥 모델의 손실 함수에 정규화 항 $\lambda\sum_{i=1}^{n}|\theta_i|$ , 또는 $\lambda\sum_{i=1}^{n}\theta_i^2$ 을 더해주면 된다.

sklearn을 사용할 경우, 다중 회귀 또는 다항 회귀 모델을 만들 때는 LinearRegression() 대신 Lasso() (L1 정규화) 또는 Ridge() (L2 정규화) 모델을 사용하면 된다.

로지스틱 회귀 모델을 구현한 LogisticRegression() 는 기본적으로 L2 정규화를 한다.
어떤 정규화 기법을 사용할지는 모델의 penalty 라는 옵셔널 파라미터로 정해 줄 수 있다. 예시는 아래와 같다.

LogisticRegression(penalty='none')  # 정규화 사용 안함
LogisticRegression(penalty='l1')  # L1 정규화 사용
LogisticRegression(penalty='l2')  # L2 정규화 사용
LogisticRegression()  # 위와 똑같음: L2 정규화 사용

참고로 딥러닝 모델에서도 정규화를 많이 사용하는데, 이때는 파라미터가 $w$ 이다. 딥러닝에서도 똑같이 정규항을 추가하면 되는데 파라미터만 바뀐다. 즉, $\lambda\sum_{i=1}^{n}|w_i|$ , 또는 $\lambda\sum_{i=1}^{n}w_i^2$ 을 더해주면 된다.

📍 L1 Regularization 과 L2 Regularization 의 차이

L1 Regularization 과 L2 Regularization 모두 좋은 가설 함수의 기준은 '데이터에 대한 오차도 작고 $\theta$ 값들도 작다.' 가 될 수 있었다.

그럼 둘의 차이점은 어떻게 될까?

L1과 L2의 차이점은 아래와 같다.

L1 정규화는 여러 $\theta$ 값들을 0으로 만들어 준다. 모델에 중요하지 않다고 생각되는 속성들을 아예 없애주는 것이다.
L2 정규화는 $\theta$ 값들을 0으로 만들기보다는 조금씩 줄여 준다. 모델에 사용되는 속성들을 L1처럼 없애지는 않는다.

그림으로 보면 다음과 같다.

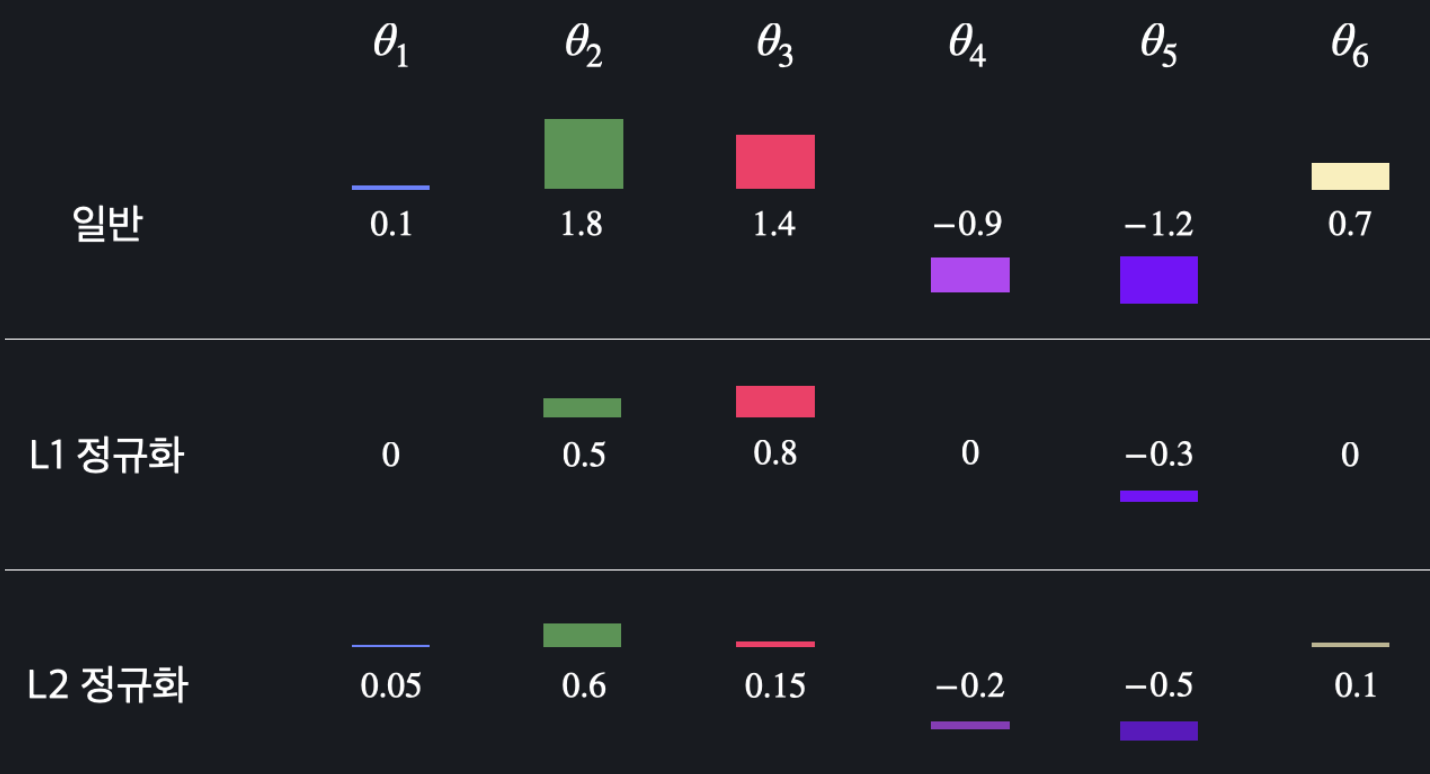
각 막대는 어떤 모델의 $\theta$ 값들을 나타낸다. 보이다시피 L1 정규화는 여러 $\theta$ 값들을 아예 0으로 만들어 버리고, L2 정규화는 전체적으로 $\theta$ 값들을 조금씩 줄여 준다.

따라서 L1 정규화는 어떤 모델에 쓰이는 속성 또는 변수의 개수를 줄이고 싶을 때 사용된다. 예를 들어 속성 20개를 사용해서 2차 다중 다항 회귀 모델을 만든다면 속성은 총 230개가 된다.

속성이 이렇게 많으면 과적합 뿐만이 아니라 모델을 학습시킬 때 많은 자원(RAM, 시간 등)을 소모할 수 있는데, 이럴 때 L1 정규화를 사용하면 많은 $\theta$ 를 0으로 만들어 주기 때문에 사용되는 속성의 개수를 많이 줄일 수 있다.
반대로 딱히 속성의 개수를 줄일 필요가 없다고 생각되면 L2 정규화를 사용하면 되는 것이다.

그러면 왜 L1 정규화는 여러 $\theta$ 값들을 0으로 만들어 주고 L2 정규화는 그러지 않는지 알아보자.

시각화를 하기 위해서 2차 다항 회귀를 예시로 보자.

h_{\theta}(x) = \theta_0 + \theta_1x + \theta_2x^2

💡 L1 정규화

먼저 L1 정규화를 보면 손실 함수는 다음과 같을 것이다.

J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \sum_{i=1}^{2}|\theta_i|

$\theta_0$ 은 정규화 항에 포함되지 않으니까 어떤 상수라고 가정하고 $\lambda$ 는 1이라고 가정한 상태이다.

그리고 이 손실 함수에서 경사 하강법을 진행하여 손실이 최소가 되는 $(\theta_1, \theta_2) = (a, b)$ 를 찾았다고 하자. 또한 정규항 $\sum_{i=1}^{2}|\theta_i|$ 의 값을 일반화 해서 $t$ 라 표현하자. 즉, $|\theta_1| + |\theta_2| = t$ 인 것이다.

이제 $\theta_1$ 과 $\theta_2$ 에 대한 평균 제곱 오차 항과 정규항을 그래프로 표현해보면 다음과 같다.

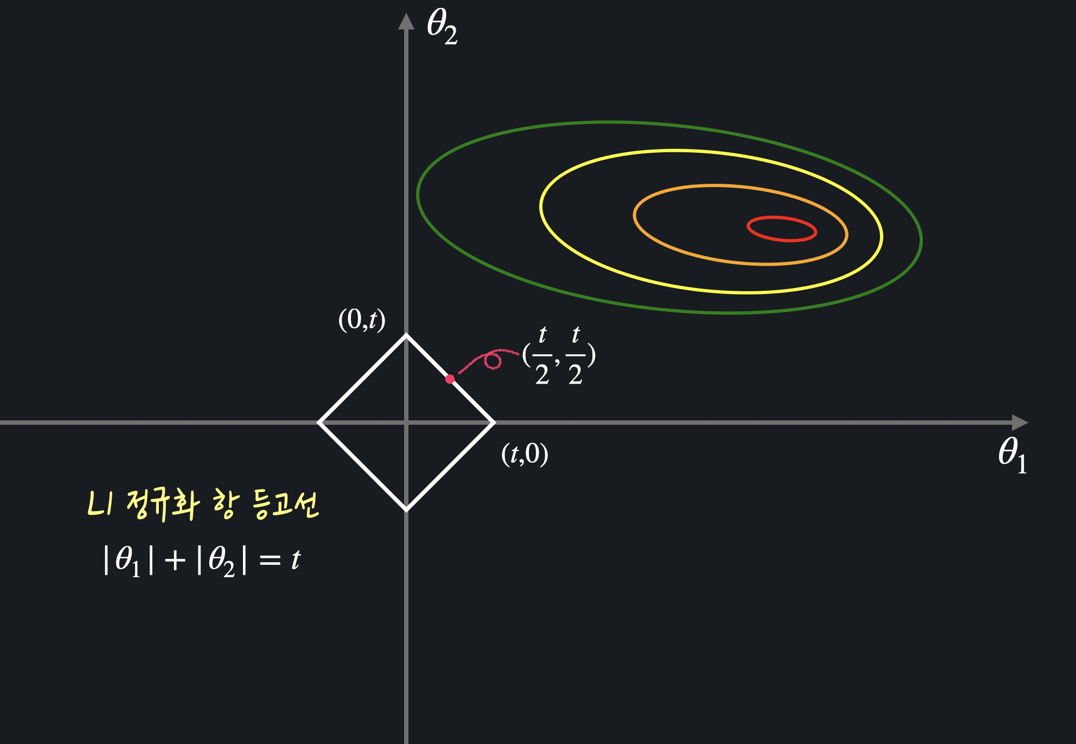
평균 제곱 오차 항 $\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2$ 을 그래프로 표현하면 이전에 봤듯이 등고선 형태로 표현할 수 있다. (복습해보면 최저점(가운데)에서 멀어질 수록 평균 제곱 오차가 커진다.)

그리고 정규항 $\sum_{i=1}^{2}|\theta_i|$ 즉, $|\theta_1| + |\theta_2| = t$ 를 그래프로 나타내면 마름모 형태가 된다.

L1 정규화에서는 이 두 항을 모두 만족하는 최적의 $\theta$ 값을 찾아야 한다. 그래서 일단 최적의 $\theta$ 값 $(a, b)$ 은 무조건 $|\theta_1| + |\theta_2| = t$ 위에 있어야 한다.
그 동시에 평균 제곱 오차 항 그래프와 만나는 지점이 되는 곳을 찾아야 하는데, 이를 표현하면 아래와 같다.

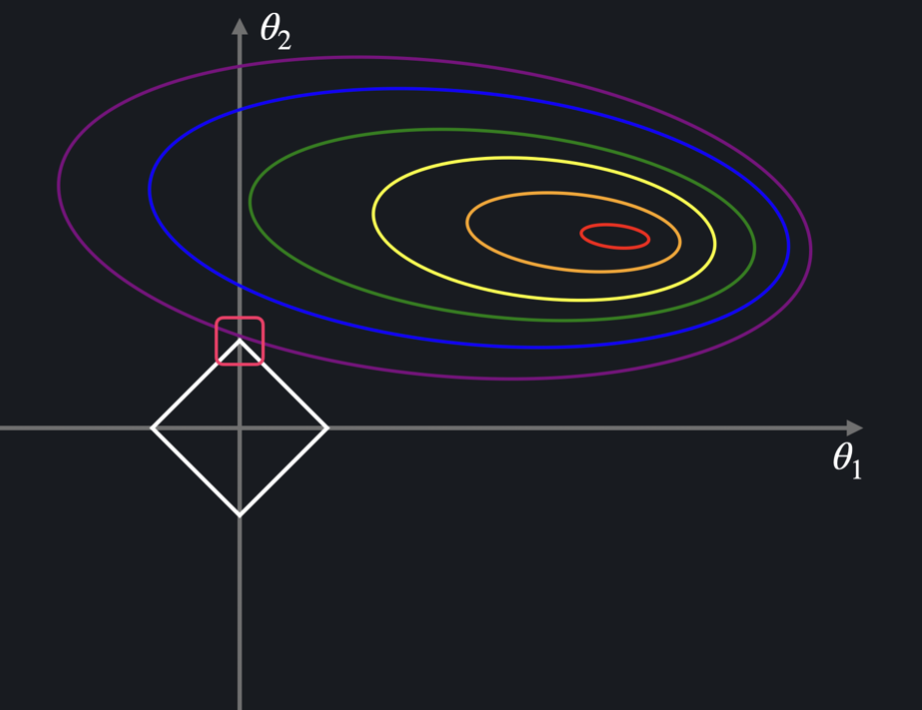
네모 표시한 곳이 평균 제곱 오차 항의 그래프와 정규항 그래프가 처음으로 만나는 지점, 즉 $\theta$ 값의 합이 $t$ 가 되면서 동시에 데이터의 오차는 최소인 지점인 것이다. 이 지점의 좌표는 $(0, t)$ 인데, 이는 정규항의 그래프가 마름모 형태이라 좌표 중 하나가 0이 될 확률이 높기 때문이다.

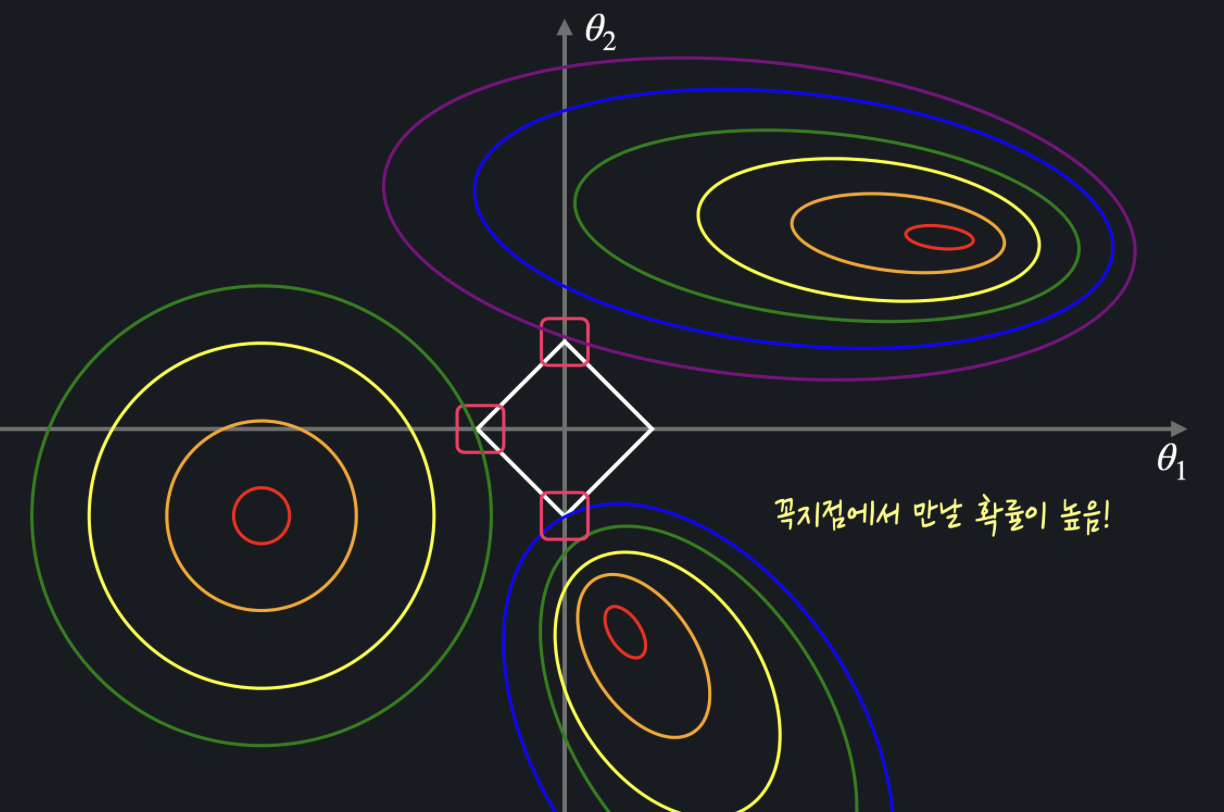
위에서 볼 수 있듯이 $t$ 의 값이 어떻고 (즉 마름모가 얼마큼 크든) 평균 제곱 오차의 그래프가 어떻게 생겼든 마름모와 평균 제곱 오차의 등고선이 닿는 지점은 꼭짓점일 확률이 높아진다.

이렇게 L1 정규화는 정규항의 그래프가 마름모 형태이기 때문에 특정 $\theta$ 값들이 0이 될 확률이 높아지게 되는 것이다.

💡 L2 정규화

이번엔 L2 정규화를 보자. L2 정규화의 손실 함수는 아래와 같다.

J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \sum_{i=1}^{2}\theta_i^2

L2 정규화에서의 정규항은 $\theta_1^2 + \theta_2^2 = t$ 로 나타낼 수 있고, 이를 그래프로 표현하면 원이 나오게 된다. 그러면 원과 평균 제곱 오차 항 그래프를 같이 놓고 보면 다음과 같다.

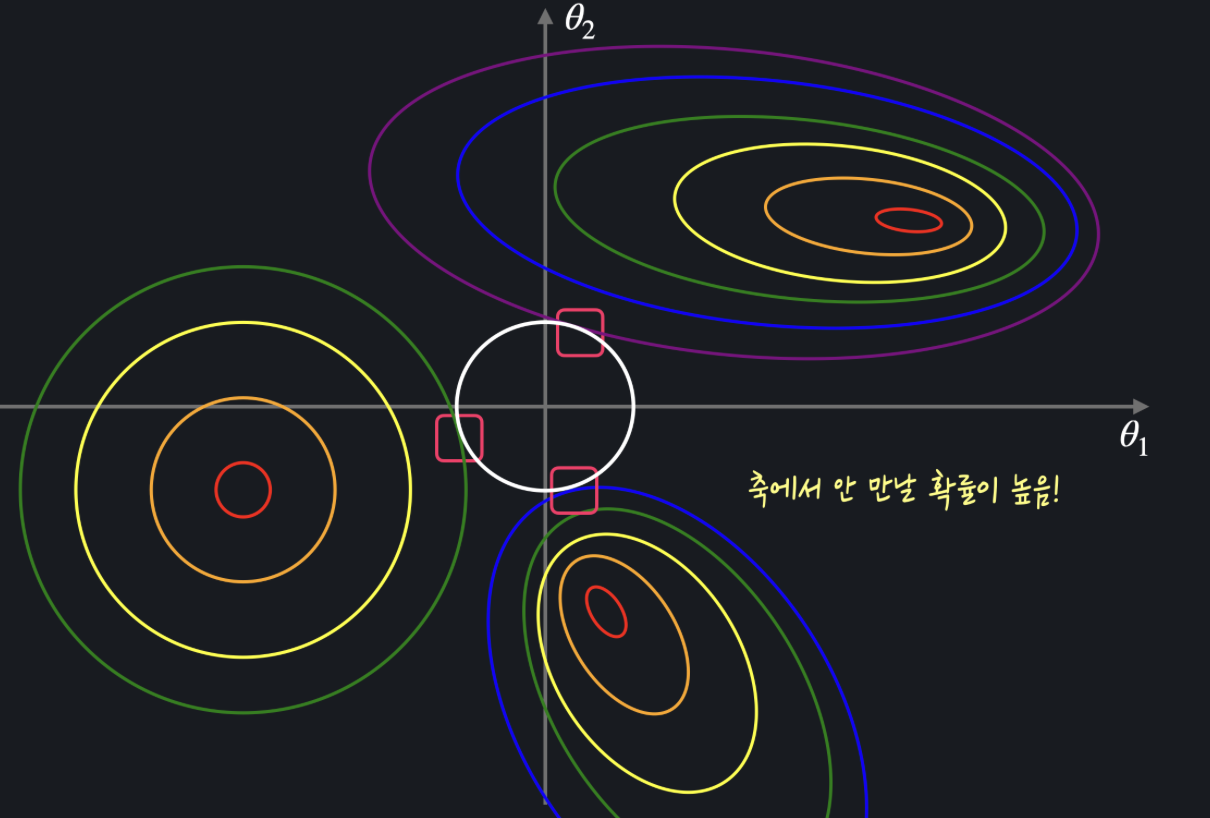
이때는 L1 때의 마름모와 달리 원 모양이기 때문에 평균 제곱 오차의 등고선과 닿는 지점이 축 위가 아닐 확률이 높다.
따라서 최적의 $\theta$ 값 $(a, b)$ 은 둘 다 0이 아닐 확률이 높은 것이다.

이러한 L1, L2 손실 함수에서 정규항의 모양이 달랐기 때문에 L1 정규화는 여러 $\theta$ 값들을 0으로 만들어 주고, L2 정규화는 그러지 않는다는 차이가 발생한 것이다.
우리는 2차항 회귀를 예시로 들었지만, 피처의 개수가 더 많아지면 위처럼 시각화하기는 힘들지만 개념은 똑같다.

출처: https://hye-z.tistory.com/23, 코드잇