ML_분류 문제

wnsdnl·2025년 3월 5일

ML 머신러닝

목록 보기

4/11

📌 분류 문제

머신 러닝은 지도 학습과 비지도 학습 그리고 강화 학습으로 나뉜다. 지도 학습은 또 회귀와 분류로 나뉘는데, 회귀는 연속적인 값을 예측하는 거고 분류는 정해진 몇 개의 값 중에 예측하는 것이다.
예를 들면 어떤 이메일이 스팸인지 아닌지, 어떤 기사가 스포츠 기사인지 정치 기사인지 연예 기사인지... 등등이 있다.

보통 분류 문제를 풀 때는 각 결괏값에 숫자 값을 지정해준다.
예를 들어서 이메일이 스팸인지 아닌지 분류한다면, 이메일에는 0이라는 값을 주고 스팸 이메일에는 1이라는 값을 준다. 이메일의 속성들을 가설 함수에 넣어서 0이 나오면 이메일이고, 1이 나오면 스팸 이메일이라고 할 수 있는 것이다.

📍 선형 회귀를 이용한 분류

공부한 시간을 갖고 시험을 통과할지 예측한다고 하자. 통과를 못한다는 걸 0이라고 표시하고, 통과한다는 걸 1이라고 표시하면 데이터를 아래와 같이 표현할 수 있다.

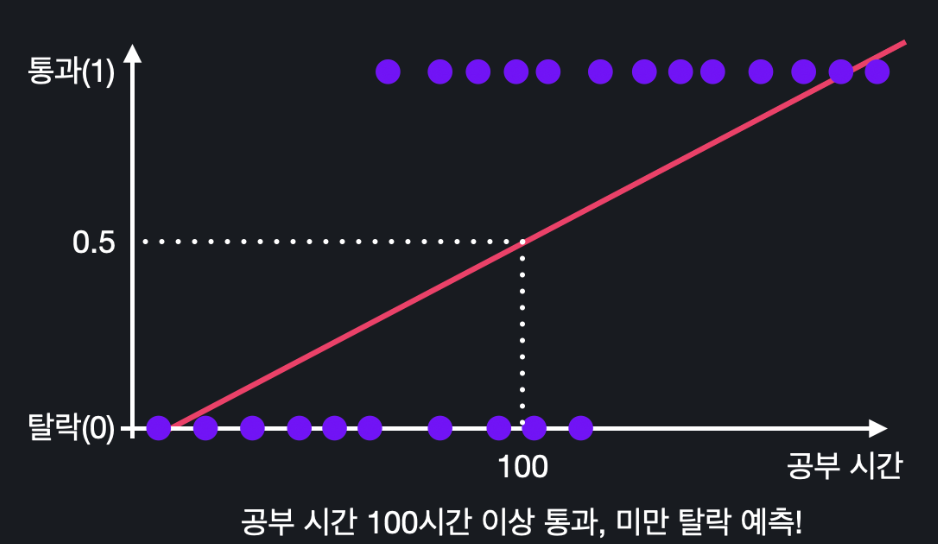
선형 회귀를 하면 이 데이터를 가장 잘 나타내는 최적선을 위와 같이 구할 수 있다.

임계치를 0.5로 하면, 0.5를 넘는 건 통과로 분류하고 0.5가 안 되는 건 통과 못한 걸로 분류할 수 있다. 지금 같은 경우에는 100시간이 딱 0.5가 되는 지점이니까, 100시간 넘게 공부한 사람은 통과로 분류하고, 100시간 밑으로 공부한 사람은 통과 못한 걸로 분류하면 되는 거다.

💡문제점

선형 회귀로 분류 문제를 풀 때는 문제가 있다. 바로 이상치에 민감하다는 것이다. 1000시간을 공부한 새로운 데이터를 추가한다고 했을 때 선형 회귀는 아래와 같이 바뀐다.

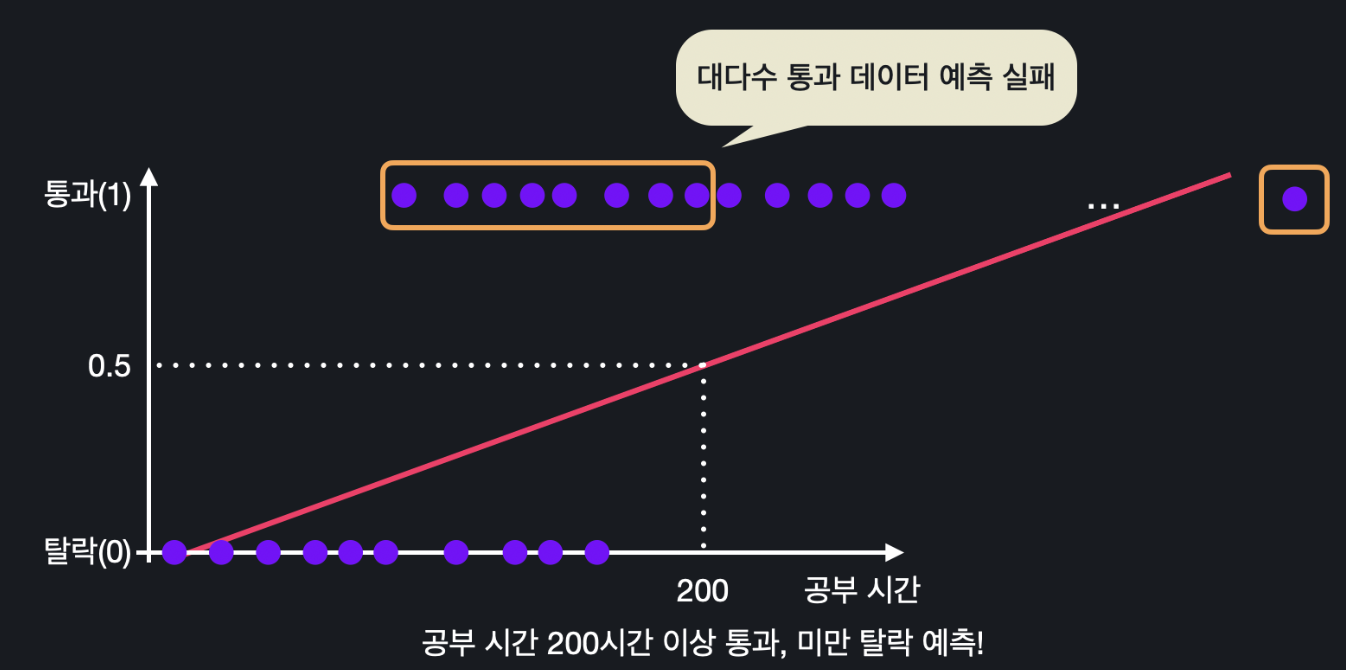
이상치 데이터로 인해 최적선이 바뀌고, 200시간이 아웃풋 0.5가 되는 지점이 된다. 데이터 상으로는 200시간 이하에도 시험을 통과한 학생이 많은데 현재 최적선으로는 200시간 이하는 모두 0.5보다 작으니 시험 탈락으로 분류해버린다. 따라서 선형 회귀로 분류를 하기에는 한계가 있다.

📍 로지스틱 회귀(Logistic Regression)를 이용한 분류

로지스틱 회귀는 데이터에 가장 잘 맞는 시그모이드 함수(Sigmoid)를 찾는 것을 의미한다. 시그모이드 함수는 아래와 같다.

S(x) = \frac{1}{1 + e^{-x}}

그래프에 그리면 아래와 같은 모양이다.

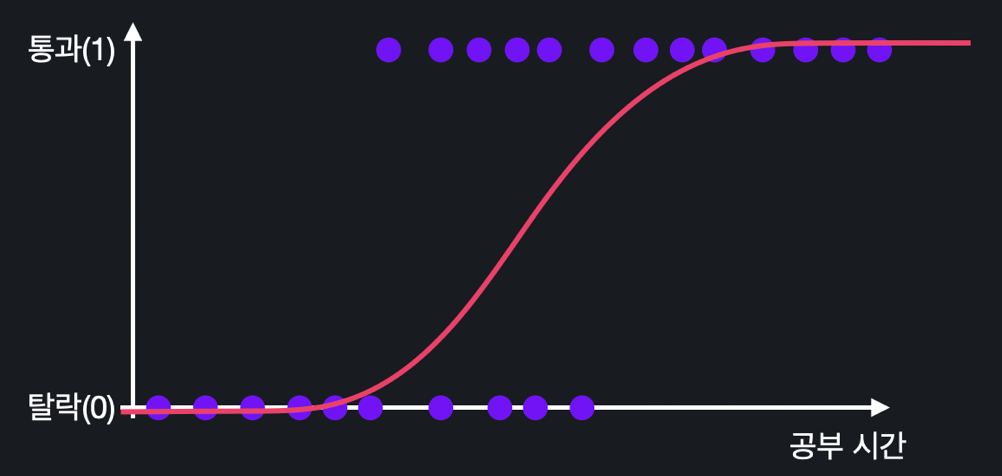
시그모이드 함수의 가장 중요한 특징 중 하나는 무조건 0과 1사이의 값을 리턴한다는 점이다. $x$ 가 양의 무한대로 갈 때는 $e^{-x}$ 가 0이 돼서 결국 1이되고, $x$ 가 음의 무한대로 갈 때는 분모가 $\infty$ 가 되어 결국 0이 된다.

결과가 0과 1 사이라는 것은 무슨 의미일까? 선형 회귀에서 쓰이는 가설 함수는 일차 함수이기 때문에 예측값이 얼마든지 커지고, 작아질 수 있다.
반면 시그모이드 함수의 결과는 항상 0과 1 사이의 값을 보장하기 때문에 이상치 데이터(예를 들면 공부 시간이 1000시간)가 생겨도 크게 영향을 받지 않는다.

💡왜 이름이 로지스틱 '회귀'?

결국 시그모이드 함수의 결과값도 0과 1사이의 연속적인 값을 리턴하기 때문에 회귀라고 볼 수 있다. 그래서 '로지스틱 분류'가 아니라 '로지스틱 회귀'라고 한다.
우리는 주로 시그모이드 함수의 결괏값이 0.5보다 큰지 작은지를 보고 결국 분류를 한다. 그러니까 이름은 로지스틱 회귀지만 사용하는 건 주로 분류라는 점을 기억하면 좋다.

📍 로지스틱 회귀 가설 함수

선형 회귀에서의 가설 함수를 벡터화 해서 표현하면 다음과 같았다.

h_{\theta}(x) = \theta^Tx

그런데 로지스틱 회귀를 할 때는 항상 아웃풋이 0과 1사이가 되도록 해야 한다. 그러기 위해서는 가설 함수 $\theta^Tx$ 를 시그모이드 함수의 인풋으로 넣어주면 된다. 즉, 시그모이드 함수를 활성화 함수(Activation Function)로써 이용하면 된다. 그러면 로지스틱 회귀의 가설 함수는 다음과 같아진다.

h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}}

활성화 함수로서 사용했기 때문에 항상 0과 1사이의 확률값이 나오게 된다. 예를 들어 공부한 시간을 바탕으로 시험을 통과할지 예측하는 분류 문제에서 입력 벡터 $x= \begin{bmatrix} x_0 \\ x_1 \end{bmatrix}$ 가 있다고 가정하자. $x_0$ 은 1로 가정하고 시작했으니 무시한다. $x_1$ 이 50이라고 할 때 이 값에 따른 가설 함수의 결과값이 0.9라면 이는 시험에 통과할 확률이 90%라는 것을 의미한다. 이는 50% 확률을 넘어섰으니 시험에 통과한 학생으로 분류를 한다. 만약 결과값이 0.3이면 확률이 30%니까 시험에 떨어진 학생으로 분류한다.

📍 로지스틱 회귀의 목적

로지스틱 회귀에서도 선형 회귀 때와 마찬가지로 가설 함수에서 최적의 $\theta$ 값을 찾아내는 것이다. 시각화를 위해서 입력 변수가 1개일 때를 봐보자.

입력 변수가 하나 일 때는 가설 함수를 $h_{\theta}(x) = \frac{1}{1 + e^{-(\theta_0 + \theta_1x)}}$ 로 나타낼 수 있다. 이 때 $\theta_0$ 은 시그모이드 함수의 평행 이동을 담당한다.

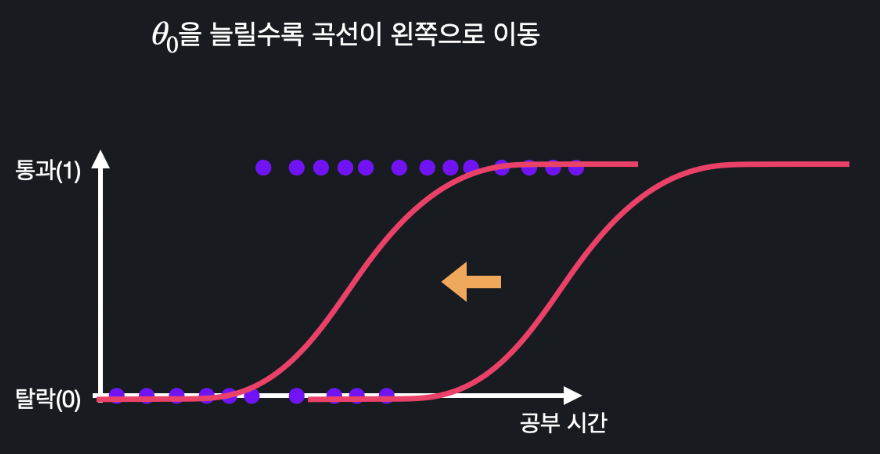
$\theta_1$ 은 시그모이드 함수의 곡선을 늘리고 줄이는 역할을 한다.

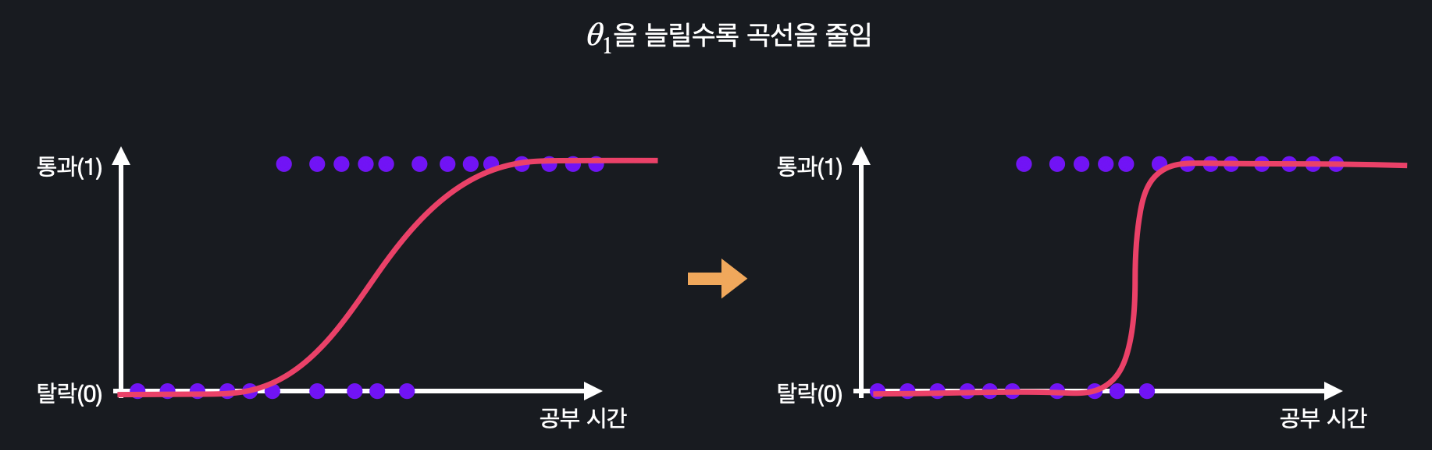
따라서 선형 회귀와 똑같이 이렇게 $\theta_0$ 과 $\theta_1$ 의 값들을 바꿔가면서 갖고 있는 학습 데이터에 가장 잘 맞는 시그모이드 모양의 가설 함수를 찾아내는 게 로지스틱 회귀의 목적인 것이다.
입력 변수가 여러 개일 때도 시각화만 어려워질 뿐, 기본적인 개념은 동일하다.

📍 결정 경계 (Decision Boundary)

Decision Boundary는 말 그대로 데이터를 분류하는 결정 경계선을 의미한다. 로지스틱 회귀에서만 사용하는 용어는 아니고, 분류를 하는 모든 문제들에 적용할 수 있는 개념이다.

속성(공부 시간)이 하나인 로지스틱 회귀 분류 문제에서는 확률이 50%, 즉 0.5가 되는 공부 시간을 찾아본다. 만약 이 시간이 47시간이라면 다음과 같이 결정 경계를 만들어 볼 수 있다.

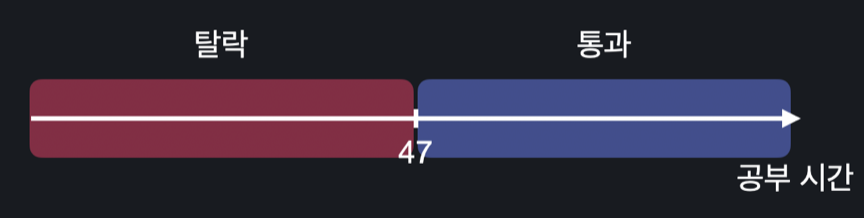
모든 데이터에 대해서 파란색 영역에 있으면, 통과, 빨간색 영역에 있으면 탈락이라고 할 수 있다. 이렇게 분류를 할 때, 분류를 구별하는 경계선을 Decision Boundary라고 부른다.

속성이 2개(공부 시간, 모의고사 성적)라면 가설 함수는 아래와 같이 될 것이다.

h_{\theta}(x) = \frac{1}{1 + e^{-(\theta_0 + \theta_1x_1 + \theta_2x_2)}}

가설 함수를 시각화 하는 것은 어렵지만, 결정 경계를 시각화 하는 것은 쉽다.

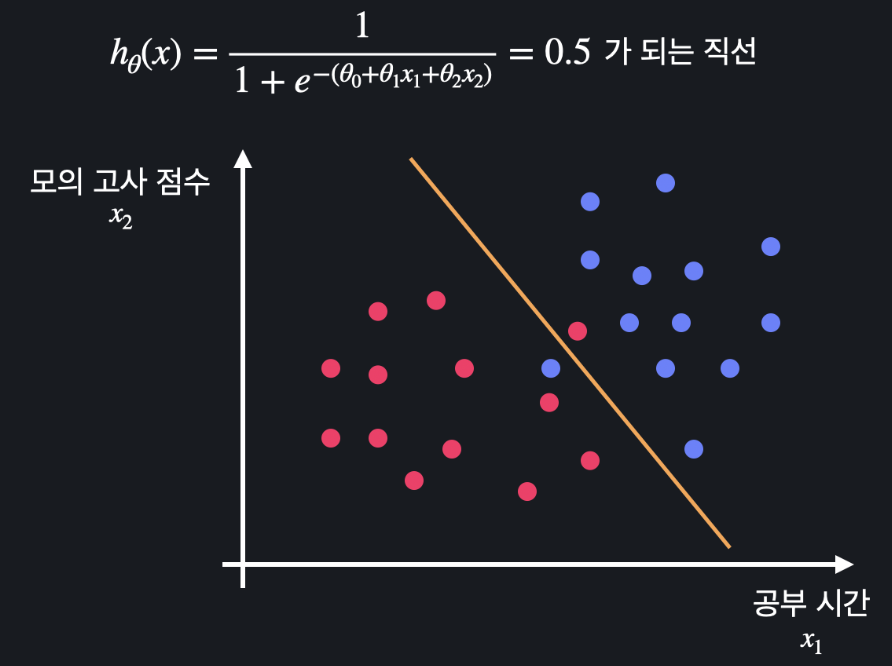
가설 함수 $h_{\theta}(x)$ 가 0.5가 되는 방정식을 풀면 $x_1$ 과 $x_2$ 의 관계식이 나오는데, 이 식이 결정 경계가 된다. 예를 들어 관계식이 $x_2 = -2x_1 + 100$ 로 나왔다면 결정 경계는 위와 같다.

Decision Boundary도 다른 개념들과 비슷하게 변수가 많아질수록 시각적으로 표현하기 힘들어진다.

📍 로그 손실 (Log-Loss / Cross Entropy)

로지스틱 회귀에서도 데이터에 잘 맞는 가설 함수를 찾고, 손실 함수를 이용해서 가설 함수를 평가하는 작업이 있다.
선형 회귀에서는 손실 함수가 MSE(평균 제곱 오차)를 기반으로 이루어졌지만 로지스틱 회귀에서는 로그 손실을 기반으로 한다. 로그 손실에 대해서 먼저 알아보자.

일단 로지스틱 회귀의 가설 함수는 다음과 같았다.

h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}}

그리고 로그 손실은 아래와 같다.

logloss(h_{\theta}(x), y) = \left\{\begin{matrix} -log(h_{\theta}(x)) \\ -log(1 - h_{\theta}(x)) \end{matrix}\right. \begin{matrix} y = 1 \\ y = 0 \end{matrix}

로그 손실을 그림으로 보면 아래와 같다.

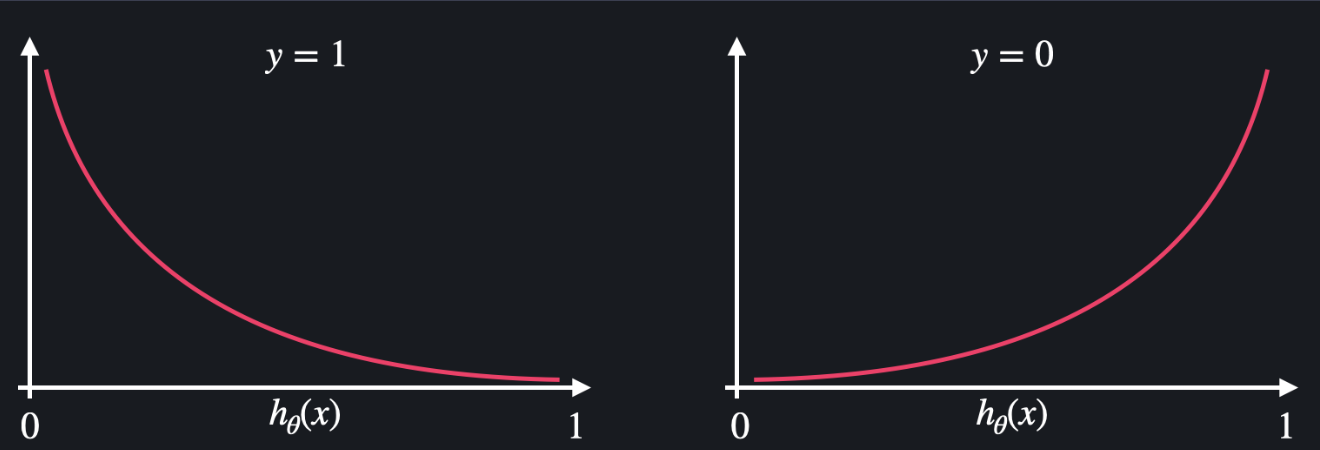
일단 $h_{\theta}(x)$ 는 입력 변수에 대한 가설함수의 예측값이고, $y$ 는 목표 값이다. 로그 손실 함수는 예측값이 실제 결과랑 얼마나 괴리가 있는지 알려 주는 역할을 한다.

그런데 로지스틱 회귀는 분류 알고리즘이다. 그리고 분류가 두 가지라고 가정하면, 가능한 목표 변수가 1과 0밖에 없다. 따라서 이 두 경우에 대해서 식이 다른 거다.

목표 값이 1인 경우, 왼쪽 그래프를 보면 된다. 가설 함수의 예측값 $h_{\theta}(x)$ 가 1에 가까운 아웃풋을 낼 수록 손실은 작아지고, 1과 먼 아웃풋을 낼 수록 더 큰 패널티를 주어 손실은 커진다.

목표 값이 0인 경우, 오른쪽 그래프를 보면 된다. 가설 함수의 예측값 $h_{\theta}(x)$ 가 0에 가까운 아웃풋을 낼 수록 손실은 작아지고, 0과 먼 아웃풋을 낼 수록 더 큰 패널티를 주어 손실은 커진다.

손실의 정도를 로그 함수로 결정하기 때문에 '로그 손실'이라고 하는 것이다.

📍 로지스틱 회귀의 손실 함수

이제 로그 손실을 알아봤으니 이걸 활용해서 로지스틱 회귀의 손실 함수를 만들어보자.
일단 보통 로지스틱 회귀의 로그 손실을 쓸 때는 다음과 같은 형식으로 사용한다.

logloss(h_{\theta}(x), y) = -ylog(h_{\theta}(x)) - (1 - y)log(1 - h_{\theta}(x))

이러면 목표 값 $y$ 가 1이든 0이든 식을 한 줄로 작성할 수 있다.

이제 로지스틱 회귀의 손실 함수를 보면 아래와 같다.

J(\theta) = \frac{1}{m}\sum_{i=1}^{m}[logloss(h_{\theta}(x^{(i)}), y^{(i)})]

우리가 하려는 건, 각 데이터에 대해서 손실을 구한 후, 손실의 평균을 내는 작업이다. 따라서 모든 학습 데이터에 대해서 로그 손실을 계산하고, 평균을 낸다. 그리고 그걸로 가설 함수를 평가하는 것이다. ( $m$ 은 학습 데이터 수)

로그 손실을 손실 함수 식에 완전히 대입하면 아래와 같이 된다.

J(\theta) = \frac{1}{m}\sum_{i=1}^{m}[-y^{(i)}log(h_{\theta}(x^{(i)})) - (1 - y^{(i)})log(1 - h_{\theta}(x^{(i)}))]

참고로 손실 함수가 $\theta$ 에 대한 식인 이유는 가설 함수의 $\theta$ 를 어떻게 바꾸냐에 따라서 학습 데이터의 손실이 결정되기 때문이다.

📍 로지스틱 회귀 경사 하강법

가설 함수와 손실 함수는 좀 다르지만, 경사 하강법을 하는 방법은 선형 회귀랑 거의 같다.

일단 임의의 $\theta$ 값을 지정한 뒤에 이전에도 봤었던 경사하강법 공식을 활용하면 된다.

\theta_i = \theta_i - \alpha \frac{\partial }{\partial \theta_i} J(\theta)

여기서 선형 회귀 때와 다른 점은 손실 함수가 다르고, 또 손실 함수 안의 가설 함수도 다르다는 것인데 신기하게도 편미분을 하면 선형 회귀 때와 동일한 꼴이 나온다.

\theta_j = \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}

단, 여기서 가설 함수 $h_{\theta}(x)$ 는 다르다. 선형 회귀에서는 일차 함수였지만, 로지스틱 회귀에서는 시그모이드 함수이다.

손실 함수의 $\theta$ 에 대한 편미분 식의 유도 과정과 $\sigma^\prime(x) = \sigma(x)(1 - \sigma(x))$ 인 이유를 증명한 노트 필기는 아래에 첨부한다. (유도 과정 중에서 편의상 $h_{\theta}(x^{(i)})$ 를 $h_i$ 로 바꿔 표기했다.)

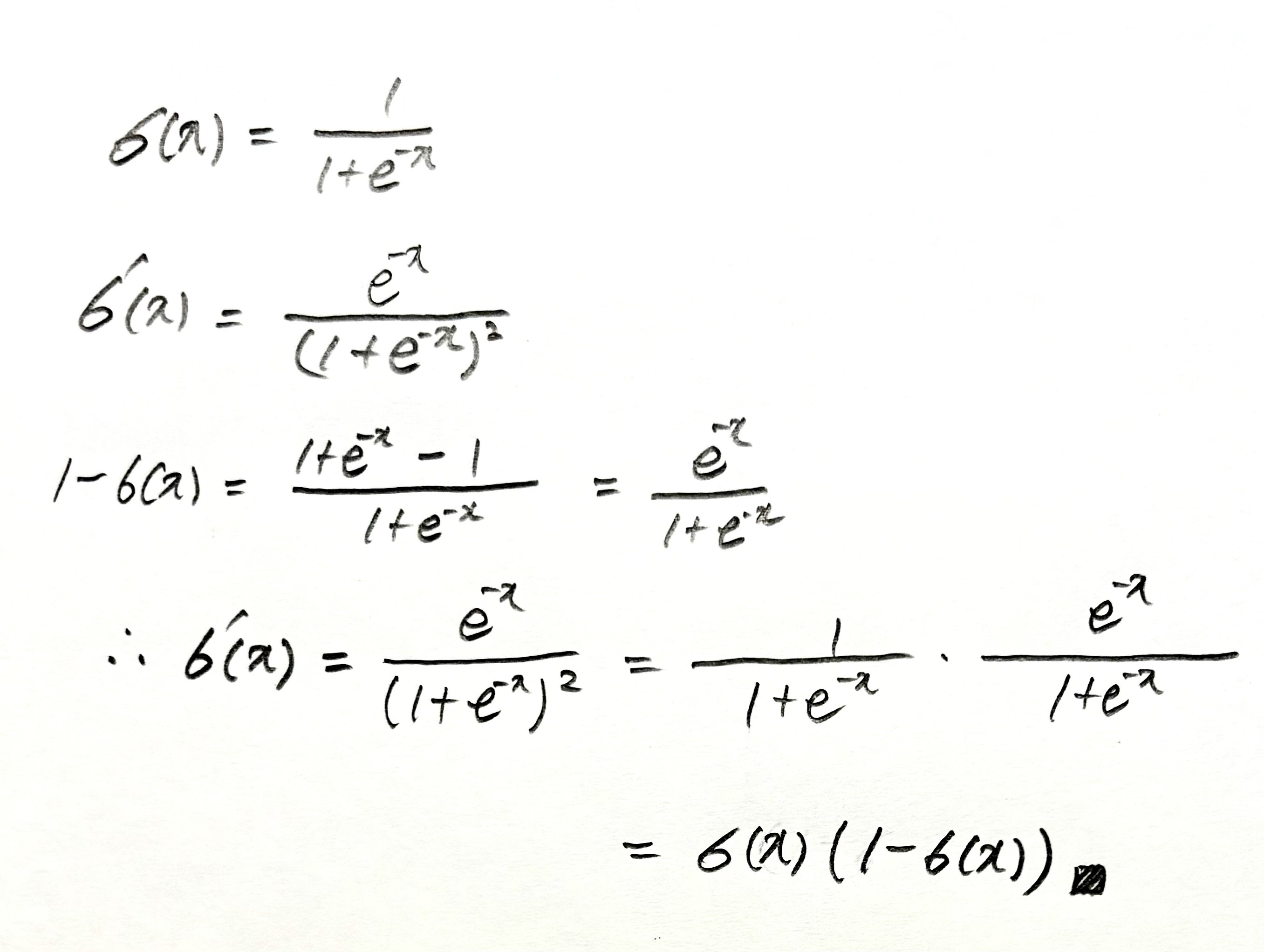
💡 Vectorization

이번에도 선형 회귀 때와 마찬가지로 로지스틱 회귀의 경사 하강법을 벡터와 행렬을 이용해 표현해보자.

일단 입력 변수와 $\theta$ 는 다음과 같이 나타낼 수 있다.

X = \begin{bmatrix} x_0^{(1)} & x_1^{(1)} & \cdots & x_n^{(1)}\\ x_0^{(2)} & x_1^{(2)} & \cdots & x_n^{(2)} \\ \vdots \\ x_0^{(m)} & x_1^{(m)} & \cdots & x_n^{(m)} \\ \end{bmatrix}

\theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \\ \end{bmatrix}

그러면 모든 데이터에 대한 예측값은 $X\theta$ 로 표현할 수 있다.

로지스틱 회귀는 가설 함수 $h_{\theta}(x)$ 가 시그모이드 함수이다. 그러면 $h_{\theta}(x)$ 를 다음과 같이 나타낼 수 있다.

sigmoid(X\theta) = \begin{bmatrix} h_{\theta}(x^{(1)}) \\ h_{\theta}(x^{(2)}) \\ \vdots \\ h_{\theta}(x^{(m)}) \\ \end{bmatrix}

목표 변수 $y$ 는 다음과 같다.

y = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \\ \end{bmatrix}

그러면 예측 오차는 다음과 같다.

error = sigmoid(X\theta) - y = \begin{bmatrix} h_{\theta}(x^{(1)}) - y^{(1)}\\ h_{\theta}(x^{(2)}) - y^{(2)}\\ \vdots \\ h_{\theta}(x^{(m)}) - y^{(m)}\\ \end{bmatrix}

그러면 로지스틱 회귀의 경사 하강법은 다음과 같이 표현할 수 있다.

\theta \leftarrow \theta - \alpha\frac{1}{m}(X^T(sigmoid(X\theta) - y))

이를 바탕으로 로지스틱 회귀 경사 하강법을 코드로 구현해보면 아래와 같다.

import numpy as np

def sigmoid(x):
    """시그모이드 함수"""
    return 1 / (1 + np.exp(-x))
    

def prediction(X, theta):
    """로지스틱 회귀 가정 함수"""
    return sigmoid(X @ theta)
    

def gradient_descent(X, theta, y, iterations, alpha):
    """로지스틱 회귀 경사 하강 알고리즘"""
    m = len(X)  # 입력 변수 개수 저장

    for _ in range(iterations):
        error = prediction(X, theta) - y
        theta = theta - (alpha / m) * (X.T @ error)
            
    return theta

# 입력 변수
hours_studied = np.array([0.2, 0.3, 0.7, 1, 1.3, 1.8, 2, 2.1, 2.2, 3, 4, 4.2, 4, 4.7, 5.0, 5.9])  # 공부 시간 (단위: 100시간)
gpa_rank = np.array([0.9, 0.95, 0.8, 0.82, 0.7, 0.6, 0.55, 0.67, 0.4, 0.3, 0.2, 0.2, 0.15, 0.18, 0.15, 0.05]) # 학년 내신 (백분률)
number_of_tries = np.array([1, 2, 2, 2, 4, 2, 2, 2, 3, 3, 3, 3, 2, 4, 1, 2])  # 시험 응시 횟수

# 목표 변수
passed = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])  # 시험 통과 여부 (0: 탈락, 1:통과)

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    hours_studied,
    gpa_rank,
    number_of_tries
]).T

# 목표 변수 y 정의
y = passed

theta = [0, 0, 0, 0]  # 파라미터 초기값 설정
theta = gradient_descent(X, theta, y, 300, 0.1)  # 경사 하강법을 사용해서 최적의 파라미터를 찾는다

최적의 세타 값:
array([-1.35280508,  1.61640725, -1.83666046, -0.60286277])

📍 분류가 3개 이상일 때

3개 이상을 분류해야 할 때는 어떻게 할까?
예를 들어 메일이 친구 관련 메일인지, 직장 관련 메일인지, 스팸 메일인지를 분류한다고 하자. 그러면 각 옵션에 0, 1, 2 라는 숫자를 붙여준다. 그래프로 나타내면 다음과 같다.

이 그래프에서 파란색 점들이 직장 메일(0), 빨간색 점들이 친구 메일(1), 그리고 주황색 점들이 스팸 이메일이다(2).

그리고 문제를 단순화하는 작업을 진행한다.
처음에는 직장 메일인지 아닌지를 분류한다. 이렇게 하면 2가지 옵션을 분류하는 문제로 바뀌니까 지금까지 배웠던 방식대로 학습시켜서 하면 된다. 그렇게 학습시켜서 구한 가설 함수를 $h_{\theta}^{(0)}(x)$ 이라 하자.
$h_{\theta}^{(0)}(x)$ 은 어떤 이메일이 직장 메일일 확률을 예측하는 가설 함수가 된다.

그 다음은 어떤 이메일이 친구 메일인지 아닌지를 분류한다. 이번에 학습시켜서 구한 가설 함수를 $h_{\theta}^{(1)}(x)$ 이라 하자.
$h_{\theta}^{(1)}(x)$ 은 어떤 이메일이 친구 메일일 확률을 예측하는 가설 함수가 된다.

마지막으로 어떤 이메일이 스팸 메일인지 아닌지를 분류한다. 이번에 학습시켜서 구한 가설 함수를 $h_{\theta}^{(2)}(x)$ 이라 하자.
$h_{\theta}^{(2)}(x)$ 은 어떤 이메일이 스팸 메일일 확률을 예측하는 가설 함수가 된다.

이렇게 3개의 가설 함수를 구한 뒤에는 예측하고 싶은 입력 변수를 3개의 가설 함수에 각각 넣는다. 그러면 그 이메일이 직장 메일일 확률, 친구 메일일 확률, 스팸 메일일 확률을 각각 구할 수 있다. 그림으로 보면 아래와 같다.

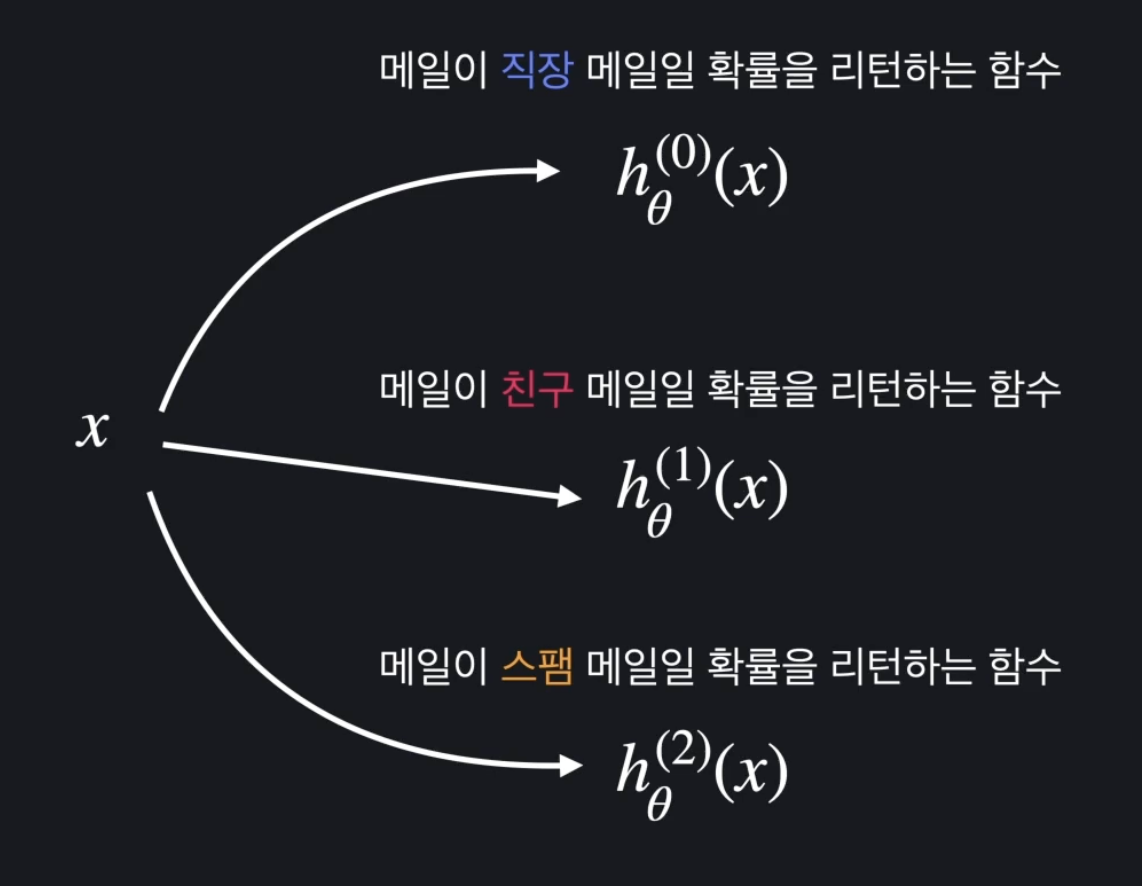
만약 $h_{\theta}^{(0)}(x) = 0.6$ , $h_{\theta}^{(1)}(x) = 0.45$ , $h_{\theta}^{(2)}(x) = 0.78$ 이 나왔다고 하자. 직장 메일일 확률이 60%, 친구 메일일 확률이 45%, 스팸 메일일 확률이 78%이고, 스팸 메일일 확률이 가장 높기 때문에 이 데이터는 스팸 메일로 분류하면 되는 것이다.

📍 로지스틱 회귀에서의 정규 방정식?

선형 회귀에서는 경사 하강법 말고도 정규 방정식으로도 최적의 $\theta$ 값들을 구할 수 있었다. 이건 로지스틱 회귀에서도 적용될까?

정답은 아니다. 이유는 뭘까?

선형 회귀에서는 손실 함수가 convex이면서 편미분 된 원소들이 모두 선형식이었기 때문에 정규 방정식과 같은 단순 행렬 연산으로 최적의 $\theta$ 값들을 구할 수 있었다.
하지만 로지스틱 회귀에서의 손실 함수는 convex이긴 하지만, 편미분 된 원소들이 비선형식이다( $\theta$ 가 $e$ 에 포함). 비선형이기 때문에 단순 행렬 연산으로는 최적의 $\theta$ 값들을 구하기 힘든 것이다.

(참고로 로그 손실, 즉 Cross-Entropy는 convex 하다.)

📍 Iris 데이터 분류 실습

sklearn 으로 Iris 데이터를 로지스틱 회귀를 통해 분류해보는 실습을 해보자.

💡 데이터 준비

from sklearn.datasets import load_iris

import pandas as pd

iris_data = load_iris()

X = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
y = pd.DataFrame(iris_data.target, columns=['class'])

💡 분류하기

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)

y_train = y_train.values.ravel() # y_train 데이터의 형태를 1차원 배열로 변환하는 역할 (2차원 배열이면 경고가 뜰 수 있음)

model = LogisticRegression(solver='saga', max_iter=2000) # 최적화 알고리즘은 saga를 사용하고 이 알고리즘을 2000번 수행(early-stopping 될 수 있음)
model.fit(X_train, y_train)

model.predict(X_test) # 모델이 테스트 데이터로 분류한 결과를 보여줌

model.score(X_test, y_test) # 모델이 테스트 데이터로 분류한 결과들에서 올바르게 분류한 샘플의 비율을 반환 (성능 확인용)

출처: 코드잇

wnsdnl

이전 포스트

ML_다항 회귀

다음 포스트