ML_다항 회귀

📌 다항 회귀 (Polynomial Regression)

다항 회귀란 데이터에 잘 맞는 일차 함수나 직선을 구하는 게 아니라 다항식이나 곡선을 구해서 학습하는 걸 의미한다.

다항 회귀도 피처가 하나인 경우, 피처가 여러 개인 경우 총 2가지로 나눌 수 있다.

📍 단순 다항 회귀

선형 회귀의 가설 함수는 다음과 같다.

만약 단순 다항 회귀의 가설 함수가 3차식이라 가정한다면 가설 함수는 아래와 같을 것이다.

다항 회귀도 선형 회귀와 마찬 가지로 최적의 $\theta_0, \theta_1, \theta_2, \theta_3$ 을 찾는 것이다. 근데 선형 회귀 때와는 다르게 삼차식이 되면서 추가로 생긴 이차항 $x^2$, 삼차항 $x^3$을 어떻게 처리해야 할까?
사실 이 단순 다항 회귀의 가설 함수 꼴은 입력 변수가 3개인 다중 선형 회귀의 가설 함수와 유사하다.

그렇다면 $x, x^2, x^3$ 을 $x_1, x_2, x_3$ 처럼 취급할 수 있다면, 사실상 다중 선형 회귀를 푸는 것과 같은 맥락이 된다. 그럼 어떻게 하면 될까?
지금은 하나의 피처만을 보고 있는 상황이니 아래 사진과 같다.

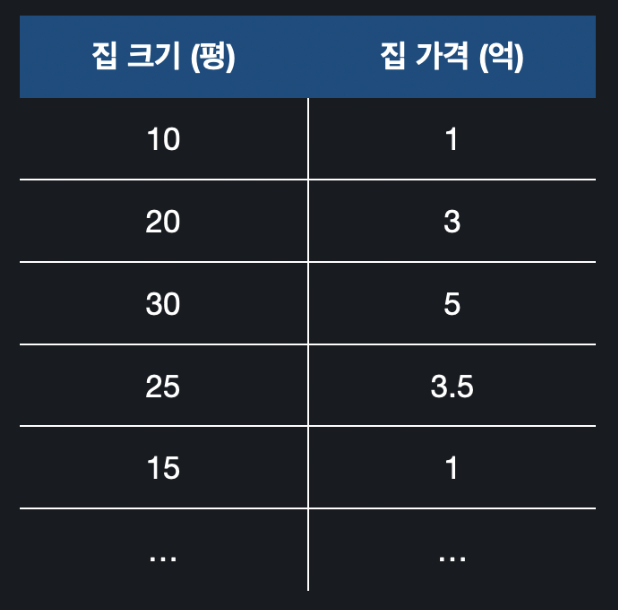
이 상태에선 $x (\approx x_1)$는 집 크기로 사용하면 되지만 $x^2(\approx x_2), x^3 (\approx x_3)$ 으로 사용할 것이 없다. 따라서 아래와 같이 가상의 열을 만들어준다.

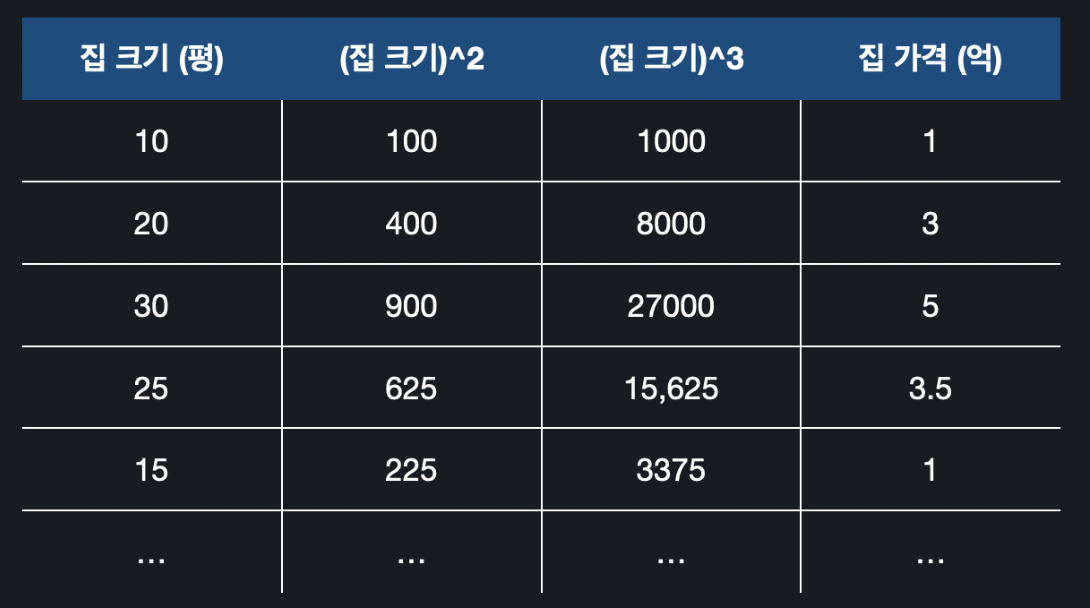
집 크기에 제곱과 세제곱을 한 가상의 열 2개를 추가하게 되면 $x^2(\approx x_2)$ 는 집 크기의 제곱, $x^3 (\approx x_3)$은 집 크기의 세제곱을 담당할 수 있게 된다. 따라서 다항 회귀를 다중 선형 회귀로 풀 수 있게되는 것이다.

📍 다중 다항 회귀

입력 변수가 여러 개인 다항 회귀는 어떻게 될까?

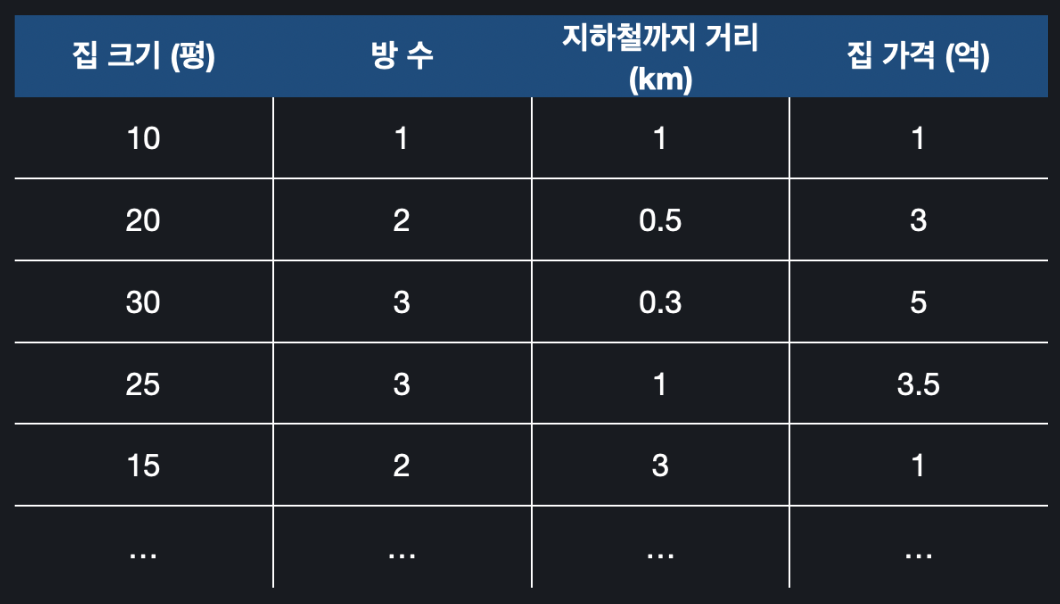
이런 상황에서 만약 다중 선형 회귀를 사용했다면 가설 함수는 $h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3$ 가 됐을 것이다.

근데 만약 데이터의 분포가 이차식과 잘 어울려서 2차 다항 회귀를 사용한다면 가설 함수 꼴은 어떻게 알 수 있을까?
일단 가설 함수의 최대 차수가 2차이기 때문에 기존의 집 크기($x_1$), 방 수($x_2$), 지하철까지 거리($x_3$)들로 만들 수 있는 모든 이차항을 알아내면 된다.

$x_1x_2$
$x_2x_3$
$x_1x_3$
$x_1^2$
$x_2^2$
$x_3^2$

이렇게 총 6개이다. 그러면 다항 회귀 가설 함수는 아래와 같이 작성해볼 수 있다.

이 2차 가설 함수를 다중 선형 회귀로 풀기 위해서 가상의 6개 열을 추가하면 된다. (이렇게 되면 $x_1x_2$를 $x_4$로, $x_2x_3$를 $x_5$로, .. 와 같이 간주할 수 있는 것이다.)

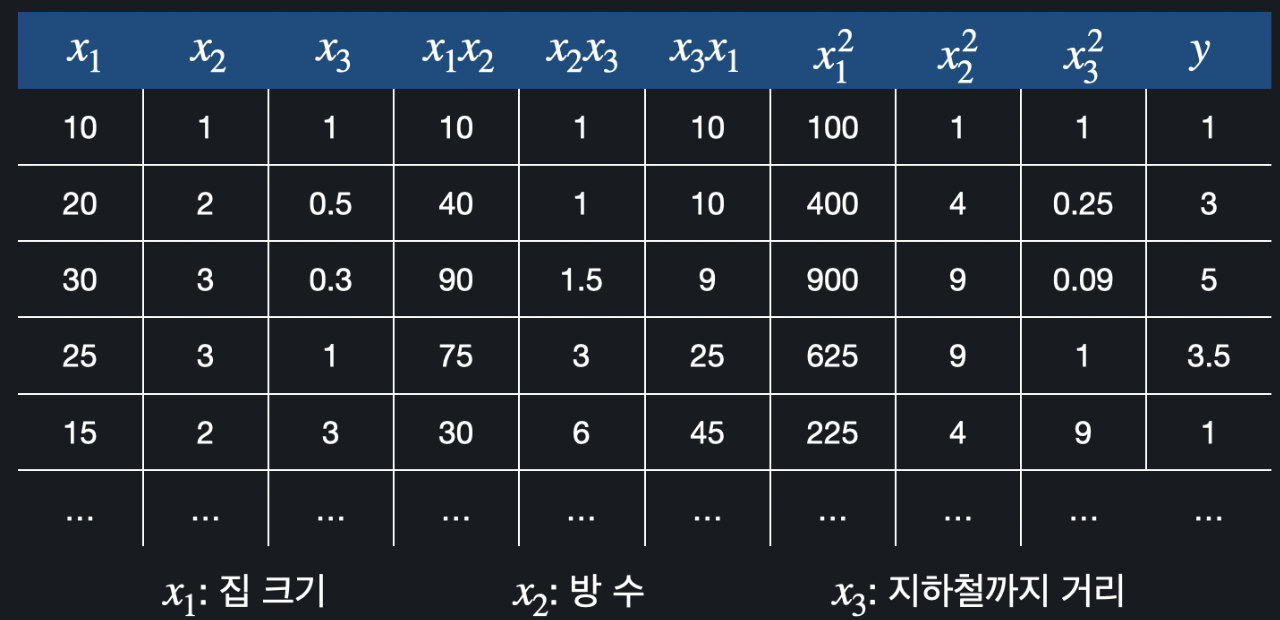
그러면 이제 이 문제를 입력 변수가 9개인 다중 선형 회귀라고 생각할 수 있다. 다항 회귀라는 생각을 하지 않고, 그냥 다중 선형 회귀인 것처럼 취급을 하고 문제를 풀면 된다.

이렇게 선형 회귀를 사용했을 때랑 다르게 다항 회귀에서는 속성끼리의 곱들을 이용해 차수를 높여준다. 속성들을 독립적으로 보는 것을 넘어서 속성끼리의 곱을 보게 되면 데이터 간의 복잡한 관계들을 학습시킬 수 있다.
다시 말해 선형 회귀 문제를 다항 회귀 문제로 만들어주면 속성들 사이에 있을 수 있는 복잡한 관계들을 프로그램에 학습시킬 수 있다.

근데 당뇨병 데이터라면 피처들은 나이, 성별, BMI, 혈압 등의 수치들이고 이는 보스턴 집 가격 데이터에 비하면 각각의 속성의 독립성이 강하다. 이럴 때는 다항 회귀 보단 다중 선형 회귀를 사용하는 것이 더 좋을 수 있다.

💡정리해보자

3개의 입력 변수로 다중 선형 회귀를 사용한다면 $h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3$이다. 근데 3차 다항 회귀를 적용해보고 싶다고 하자. 그럼 가설 함수의 최고차항은 3차이다. 기존 입력 변수 3개로 만들 수 있는 모든 3차항 조합을 만들어낸다.(피처 간의 관계를 모두 파악하기 위해 모든 조합을 봄) 그렇게 탄생한 3차 가설 함수를 다중 선형 회귀로 풀기 위해 방금 봤던 모든 3차항 조합으로 가상의 열들을 추가한다. 이렇게 되면 2차, 3차와 같은 항들(ex. $x_2^2, x_1x_2x_3$)이 일차항들(ex. $x_2, x_5$)로 간주가 되고, 결국 다중 선형 회귀를 푸는 것과 동일해진다.

그렇게 되면 기존 다중 선형 회귀는 입력 변수가 4개였는데, 다항 회귀를 적용하기 위해 탄생시킨 다중 선형 회귀는 입력 변수가 10개 이상이 된다. 이 말은 즉슨 다중 선형 회귀보다 더 많은 변수 간의 상관관계를 파악하기 위한 입력 변수(피처들 간의 곱)를 탄생시켰고 이로써 데이터를 더 잘 학습시킬 수 있게 된다.

다만 차수를 너무 올리면 훈련 데이터에 과적합 되어 일반화 성능이 떨어지니 주의해야 하고, 위에서 말했던 것처럼 속성 간의 독립성이 명백히 강하다면 굳이 다항 회귀를 쓸 이유가 없다. (서로 연관 없는 속성들에 대한 곱으로 필요없는 $\theta$ 까지 학습시키기엔 부담이 될 수 있는데, 이 때는 L1 regression을 사용하여 학습을 하면서 필요가 없는 속성들의 $\theta$ 값들을 0으로 만들어줄 수 있다.)

구현 코드는 아래와 같다. 모델 학습은 다중 선형 회귀와 동일하기에 생략한다.

from sklearn.preprocessing import PolynomialFeatures

polynomial_transformer = PolynomialFeatures(2) # 다항 회귀를 위해 데이터를 가공해 주는 역할을 함. 원하는 가설 함수 차수를 넣으면 됨

polynomial_data = polynomial_transformer.fit_transform(X) # 기존 데이터 X를 2차 다항 회귀의 가설 함수로 쓸 수 있도록 가상의 열들을 추가해줌

polynomial_feature_names = polynomial_transformer.get_feature_names_out(X.columns) # 실제로 만든 가상의 열들을 보여준다.

X = pd.DataFrame(polynomial_data, columns=polynomial_feature_names) # 이제 다항 회귀를 위한 새로운 데이터셋이 준비됐다.

실제로 추가된 가상의 열들을 확인해보면 다음과 같다.

array(['1', 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
       'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'CRIM^2', 'CRIM ZN',
       'CRIM INDUS', 'CRIM CHAS', 'CRIM NOX', 'CRIM RM', 'CRIM AGE',
       'CRIM DIS', 'CRIM RAD', 'CRIM TAX', 'CRIM PTRATIO', 'CRIM B',
       'CRIM LSTAT', 'ZN^2', 'ZN INDUS', 'ZN CHAS', 'ZN NOX', 'ZN RM',
       'ZN AGE', 'ZN DIS', 'ZN RAD', 'ZN TAX', 'ZN PTRATIO', 'ZN B',
       'ZN LSTAT', 'INDUS^2', 'INDUS CHAS', 'INDUS NOX', 'INDUS RM',
       'INDUS AGE', 'INDUS DIS', 'INDUS RAD', 'INDUS TAX',
       'INDUS PTRATIO', 'INDUS B', 'INDUS LSTAT', 'CHAS^2', 'CHAS NOX',
       'CHAS RM', 'CHAS AGE', 'CHAS DIS', 'CHAS RAD', 'CHAS TAX',
       'CHAS PTRATIO', 'CHAS B', 'CHAS LSTAT', 'NOX^2', 'NOX RM',
       'NOX AGE', 'NOX DIS', 'NOX RAD', 'NOX TAX', 'NOX PTRATIO', 'NOX B',
       'NOX LSTAT', 'RM^2', 'RM AGE', 'RM DIS', 'RM RAD', 'RM TAX',
       'RM PTRATIO', 'RM B', 'RM LSTAT', 'AGE^2', 'AGE DIS', 'AGE RAD',
       'AGE TAX', 'AGE PTRATIO', 'AGE B', 'AGE LSTAT', 'DIS^2', 'DIS RAD',
       'DIS TAX', 'DIS PTRATIO', 'DIS B', 'DIS LSTAT', 'RAD^2', 'RAD TAX',
       'RAD PTRATIO', 'RAD B', 'RAD LSTAT', 'TAX^2', 'TAX PTRATIO',
       'TAX B', 'TAX LSTAT', 'PTRATIO^2', 'PTRATIO B', 'PTRATIO LSTAT',
       'B^2', 'B LSTAT', 'LSTAT^2'], dtype=object)

보면 PTRATIO^2, RM PTRATIO 와 같이 가능한 모든 이차항 조합을 만들어낸 걸 볼 수 있다.

---

출처: 코드잇