ML_추천시스템

wnsdnl·2025년 7월 30일

머신러닝 추천시스템

ML 머신러닝

목록 보기

10/11

📌추천 시스템

📍추천 시스템이란?

수많은 상품들 사이에서 사용자가 좋아해 할 만한 것들을 찾아주는 프로그램을 추천 시스템이라고 한다.

구체적으로 말하면,
어떤 추천을 할 때, 유저의 행동 패턴을 통해 그 작업에 대한 추천을 더 정확하게 해주는 머신러닝 프로그램이라고 볼 수 있다.

어떤 데이터로 어떻게 추천을 하는지 간단하게만 보고 넘어가보자.

📍추천 시스템 데이터

유저에게 영화를 추천해주는 예시를 들어볼 때 가장 대표적으로는 평점 데이터(Rating data)가 있다.

위의 사진과 같이 각 행에는 유저를, 각 열에는 영화를 쓰고, 각 유저가 해당 영화에 1부터 5까지의 평점을 매긴 것을 나타낸다. 이때 숫자가 높을 수록 좋은 평점이고, 숫자가 낮을 수록 안 좋은 평점이다.

유저는 모든 영화에 평점을 매길 수 없는 것이 정상이다. 따라서 위 사진처럼 유저가 평점을 매기지 않은 빈 공간이 있다.

추천 시스템의 목표는 이미 주어진 평점들을 기반으로 이 빈칸들의 값을 예측하는 것이다. 만약 빈칸을 아래 사진과 같이 예측했다고 가정하자.

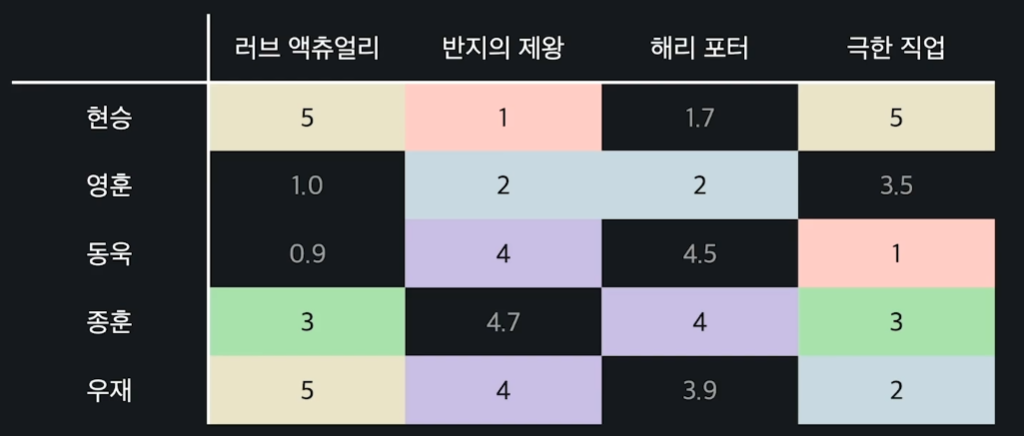
이렇게 됐을 때 평점이 4점 이상으로 예측된 영화들만 추천한다고 하면, 우리는 동욱에게 해리포터를 추천할 수 있고, 종훈에게는 반지의 제왕을 추천할 수 있게된다.

정리하자면 추천 시스템은

유저와 상품의 관계를 표현한 데이터를 사용하고,
유저와 상호작용이 없었던 상품에 대한 선호도를 예측하며,
선호도가 높게 예측되는 상품들을 유저에게 추천해주는 방식이다.

근데 추천 시스템에서 꼭 평점 데이터만을 사용하는 것은 아니다. 다음 두 가지 형태의 데이터를 알아보자.

직접 데이터(explicit data)
직접 데이터는 유저가 직접적으로 상품에 대한 만족/선호도를 표시한 데이터이다.
따라서 방금 보았던 영화 유저 평점 데이터도 유저가 직접 영화에 대해서 1부터 5까지의 선호도를 표시했기 때문에 직접 데이터로 볼 수 있다.
유튜브 같은 경우에는 영상에 대해서 시청자가 좋아요/싫어요 를 표시한다. 이는 영상에 대해서 좋아요(1)와 싫어요(0)로 선호도를 직접 표시한 것이기 때문에 이것도 직접 데이터에 해당한다.
간접 데이터(implicit data)
간접 데이터는 유저가 직접적으로 선호도를 표시하지 않았지만 유추할 수 있는 데이터이다.
예를 들어 유저가 유튜브에서 어떤 영상을 시청했는지에 대한 유저의 영상 시청 데이터라든지, 페이스북에서 누구와 친구를 맺었는지에 대한 데이터라든지, 또는 아마존에서 어떤 상품을 구매했는지에 대한 데이터라든지, 등이 있다.
간접 데이터도 똑같이 유저와 상품의 관계를 행렬로 표현한다.

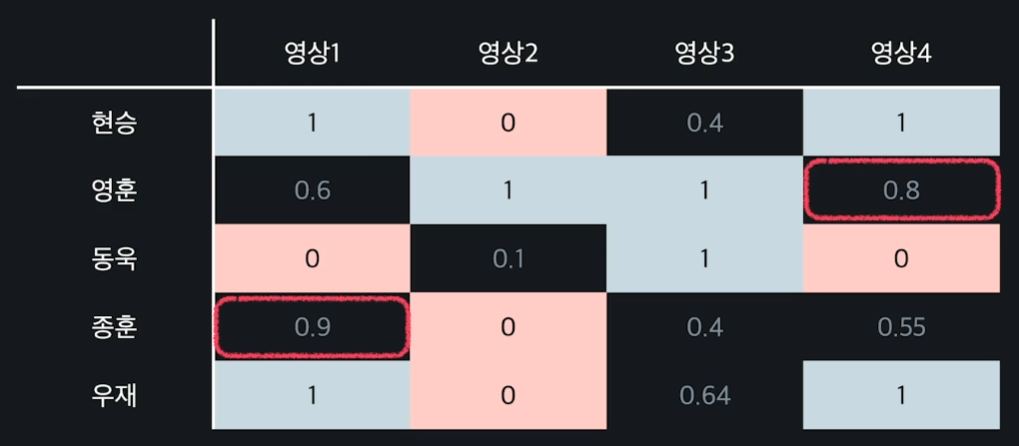
예를 들어 유튜브 시청 데이터가 위와 같다고 해보자.
앞서 말한대로 간접 데이터도 똑같이 행렬을 이용해서 관계를 표현한다. 시청을 했다면 1, 썸네일은 봤지만 시청하지 않은 영상은 0으로 나타낸다.
이때도 마찬가지로 빈칸을 예측하고 예측값이 1에 가까운 영상들(빨간 박스)을 해당 유저에게 추천하면 되는 것이다.

이러한 직접 데이터와 간접 데이터는 저마다 장단점이 있다.

직접 데이터
- 장점 : 유저의 선호도를 정확히 나타낸다.
  유저로부터 상품의 선호도를 직접적으로 받기 때문에 유저의 선호도를 정확히 나타낸다.
- 단점 : 데이터를 수집하기 어렵다.
  만약 사용자가 리뷰를 잘 남기지 않거나, 영상에 좋아요나 싫어요를 잘 달지 않는 성향이라면 직접적인 데이터는 수집이 잘 안되기 때문에 추천 시스템이 학습할 때 데이터 부족으로 어려움을 겪는다.
간접 데이터
- 장점 : 데이터를 수집하기 쉽다.
  사용자가 상품을 구매하거나 영상을 시청하는 행위는 직접적으로 선호도를 남기는 행위보다 비교적 더 많이 일어나므로, 간접 데이터는 직접 데이터에 비해서 수집이 훨씬 쉽다.
  (정확한 적은 양의 데이터보다, 조금 부정확하지만 많은 양의 데이터로 학습하는 것이 더 정확할 수 있다.)
- 단점 : 해당 데이터가 명확하지 않을 수 있다.
  왜냐하면 쿠팡에서 어떤 물건을 샀어도 실제론 만족도가 낮을 수 있으며, 갖고 싶지만 아직 사지 않은 상품도 있을 것이다. 또 영상은 시청했지만, 영상이 맘에 들지 않았을 수도 있기 때문이다.

일단은 직접 데이터를 위주로 한 번 알아보자.

📍내용 기반 추천

내용 기반 추천은 상품의 내용(특성)을 기반으로 추천하는 방법을 말하며, 구체적으로는 상품의 속성, 즉 '어떤' 상품인지를 사용해서 추천한다.

예를 들어 영화 속성 데이터가 다음과 같다고 하자.

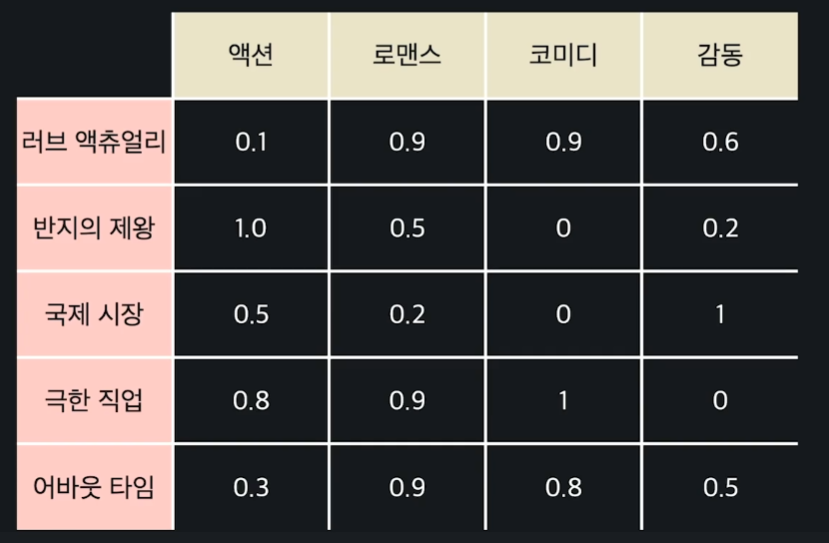
극한 직업 같은 경우에는 감동에 대한 수치가 0이므로 감동적인 부분은 없다는 의미이고, 코미디에 대한 수치는 1이므로 코미디 요소가 주를 이룬다는 뜻이다.
이렇게 0부터 1까지의 수로 해당 영화가 각각의 속성들을 얼마만큼 차지하는지를 나타낸다.

일단은 유저 한 명에 대한 추천 시스템을 만든다고 가정하자. 현승이가 평가한 각 영화의 평점을 열로 이어 붙인다. 영화 극한 직업에는 현승이가 평점을 매기지 않아서 극한 직업에 대한 행은 제거해주었다. 이렇게 해서 만들어진 테이블은 아래와 같다.

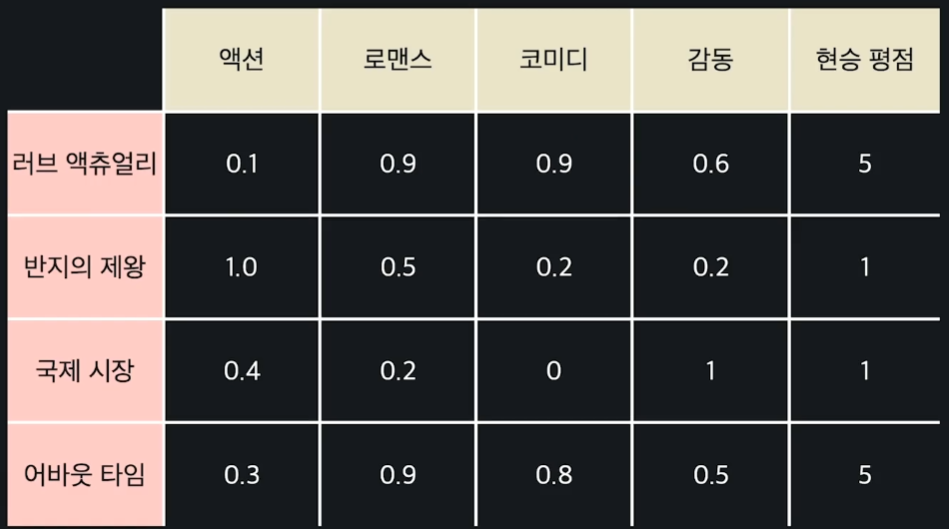
이런 테이블에서 액션, 로맨스, 코미디, 감동 속성을 입력 변수 $x$ 로 두고, 현승의 평점을 목표 변수 $y$ 로 둔다.
그러면 새로운 영화에 대한 현승의 평점을 예측할 수 있는 머신러닝 프로그램을 만들어볼 수 있다.

만약 영화가 좋다/나쁘다 에 대한 데이터라면 분류 알고리즘을 사용하면 될 것이고, 지금처럼 1~5까지의 연속적인 수를 다루는 데이터라면 회귀 알고리즘을 사용하면 될 것이다.

선형회귀나 다항 회귀 등 여러 가지를 사용해도 문제 없지만 일단 지금은 선형회귀를 사용하는 것으로 한다.

속성이 1개 이상으므로 다중 선형 회귀를 사용하면 되고, 그 식은 아래와 같다.

h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_4

더 쉽게 표현하면 아래와 같다.

h_\theta(x) = \theta^Tx

경사 하강법을 통해 유저 현승에 대한 $\theta$ 값들을 다음과 같이 구했다고 하자.

\theta = \begin{bmatrix} -0.5 \\ 1 \\ 3 \\ 3.5 \\ -2 \\ \end{bmatrix}

이는 유저 현승이가 각각 액션, 로맨스, 코미디, 감동 영화를 이 만큼씩 좋아한다고 나타내고 있는 것이다.

이때 만약 새로운 영화인 "러브 액츄얼리"에 대한 영화 속성 데이터가 다음과 같다고 하자.

x = \begin{bmatrix} 1 \\ 0.1 \\ 0.9 \\ 0.7 \\ 0 \\ \end{bmatrix}

이를 이용하여 $\theta$ 와 $x$ 를 $h_\theta(x) = \theta^Tx$ 에 대입하면 4.75가 나오는데, 이는 현승의 "러브 액츄얼리"에 대한 예측 평점이다.

이런 식으로 유저가 평가하지 않은 모든 영화들에 대해서 예측 값을 계산한다. 그리고 예측한 영화들 중 예측 평점이 가장 높은 k개의 영화를 유저에게 추천해주면 되는 것이다.

지금은 문제를 단순화하기 위해 유저가 한 명인 경우만을 보고 있었는데, 내용 기반 추천을 할 때는 모든 유저마다 이 과정을 반복하면 된다.

📍내용 기반 추천의 장단점

장점
- 한 유저에게 상품을 추천할 때, 다른 유저의 데이터가 필요하지 않다.
- 새롭게 출시한 상품이나, 비인기 상품을 추천해줄 수 있다.
단점
- 상품에 대한 적합한 속성을 고르는 게 힘들 수 있다. 사람마다 해당 상품을 좋아하는 이유가 모두 다르기 때문에, 학습에 어떤 속성을 사용해야 하는지 정확히 알기 어렵다.
- 고른 속성들의 값이 주관적으로 선정될 수 있다.
- 학습된 유저의 행동범위 밖에 있는 상품들을 추천해주기 어렵다.
- 다른 사람들도 좋게 평가한 인기 상품들을 더 추천해줄 수 없다.

📍협업 필터링

내용 기반 추천의 대표적인 특징 중 하나는 한 유저의 평점이 다른 유저의 평점에 영향을 미치지 않는다는 점이었다.

그치만 실제로 유저들의 평점이 정말 독립적이라 볼 수 있을까?

예를 들어 유저1과 유저2가 영화에 매긴 평점들이 비슷하다면, 새로운 영화에 대한 유저1의 평점을 바탕으로 유저2의 평점까지 예측해볼 수 있을 것이다.

이처럼 실제로는 유저들의 평점은 서로 독립적이지 않으며, 이러한 점을 고려하여 '한 명의 유저에게 영화를 추천해줄 때, 다른 유저들의 데이터도 사용하는 방식'을 협업 필터링이라고 한다. 즉, 수많은 유저 데이터들이 서로 협업을 해서 추천하는데 도움을 준다는 의미이다.

협업 필터링을 하는 가장 간단한 방식을 살펴보자.

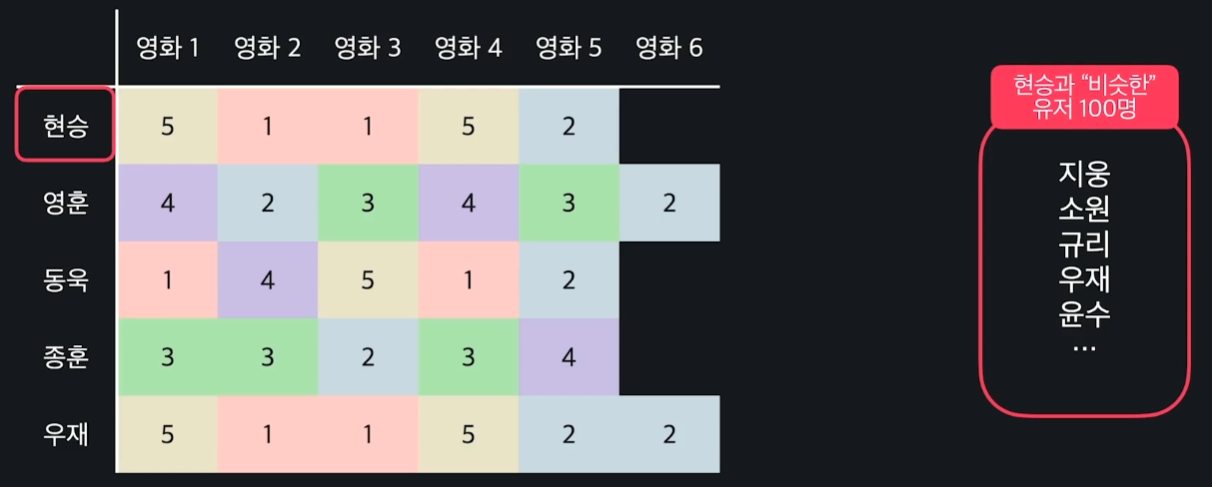
먼저 현승과 영화 평점을 비슷하게 한 유저 n명을 뽑는다. 그러면 비슷한 유저들끼리는 비슷한 영화를 좋아한다는 가정을 바탕으로, 현승이 평가하지 않은 영화들의 평점을 비슷한 유저들이 평가한 영화들을 기반으로 예측을 한다.

따라서 유저 n명의 영화 6에 대한 평점의 평균을 현승의 영화 6에 대한 예측 평점값으로 사용하면 되는 것이다.
현승이 평가하지 않은 다른 영화들에도 같은 방식으로 평점을 예측하고, 이들 중 예측 평점이 가장 높은 k개를 현승에게 추천하면 된다.

이제 이런 방식을 구체적으로 어떻게 할 수 있는지를 알아보자.

먼저 다음과 같은 평점 테이블이 있다고 할 때, 데이터를 어떻게 표현할 수 있을지 알아보자.

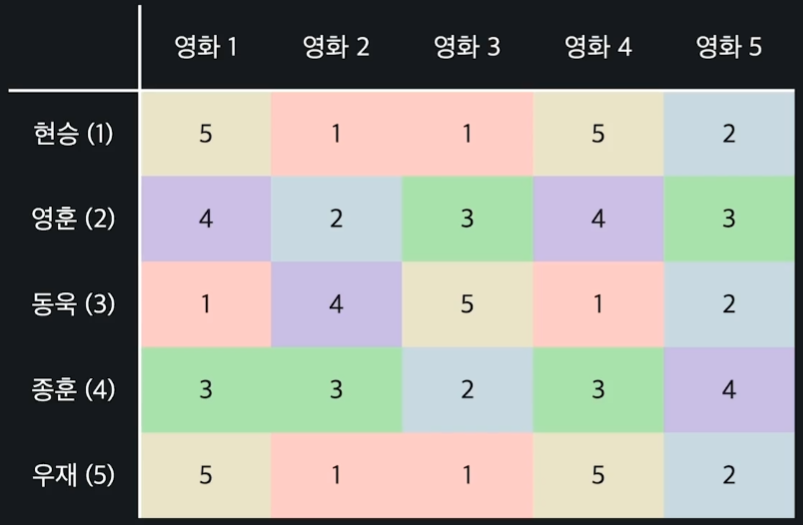
벡터를 사용하여 한 유저가 남긴 영화들의 평점을 표현할 수 있는데, 예를 들어 유저 현승의 평점 벡터 $r$ 은 아래와 같이 표현해볼 수 있다.

r^{(1)} = \begin{bmatrix} 5 \\ 1 \\ 1 \\ 5 \\ 2 \end{bmatrix}

일반화 해서 유저 $a$ 의 평점 벡터 $r$ 은 $r^{(a)}$ 과 같이 표현할 수 있다. 또 유저 $a$ 가 영화 $i$ 에 준 평점은 $r^{(a)}_i$ 으로 나타낼 수 있을 것이다.

이제 이렇게 표현한 평점 벡터들 중에서 어떻게 비슷한 벡터들끼리 정의할 수 있을까?

크게 유클리드 거리 방법과 코사인 유사도 방법이 있다

📍비슷한 유저 정의I : 유클리드 거리

유클리드 거리 방법을 이용할 때는 거리가 가까울수록(작을수록) 비슷하고, 거리가 멀수록(클수록) 비슷하지 않다고 보면 된다. 예를 들어 3명의 유저들의 평점 벡터가 다음과 같다고 하자.

r^{(a)} = \begin{bmatrix} 4 \\ 3 \\ 5 \\ 2 \\ 4 \end{bmatrix} , r^{(b)} = \begin{bmatrix} 4 \\ 4 \\ 4 \\ 3 \\ 4 \end{bmatrix} , r^{(c)} = \begin{bmatrix} 1 \\ 5 \\ 1 \\ 5 \\ 3 \end{bmatrix}

여기서 다음과 같은 유클리드 거리 공식을 적용한다.

dist(a, b) = \sqrt{\sum_{i=1}^{n}(r^{(a)}_i - r^{(b)}_i)^2}

이를 바탕으로 먼저 유저 $a$ 와 유저 $b$ 의 거리를 구해준다. ( $\approx 1.73$ )

그리고 유저 $a$ 와 유저 $c$ 의 거리를 구해준다. ( $\approx 6.24$ )

결과를 바탕으로 유저 $a$ 와 유저 $b$ 의 거리가 더 가깝다는 것을 알 수 있다. 육안으로 봐도 유저 $a$ 와 유저 $b$ 의 평점들이 비슷한 것을 확인할 수 있다.

📍비슷한 유저 정의I : 코사인 유사도

\begin{bmatrix} 4 \\ 1 \\ \end{bmatrix} , \begin{bmatrix} 1 \\ 3 \\ \end{bmatrix}

위와 같은 두 벡터가 있고 거리를 통해 이 유저들이 서로 얼마나 비슷한지를 계산했을 때는 이 데이터를 점으로 나타냈다.

코사인 유사도를 사용할 때는 이 데이터들을 아래와 같이 선으로 나타낸다.

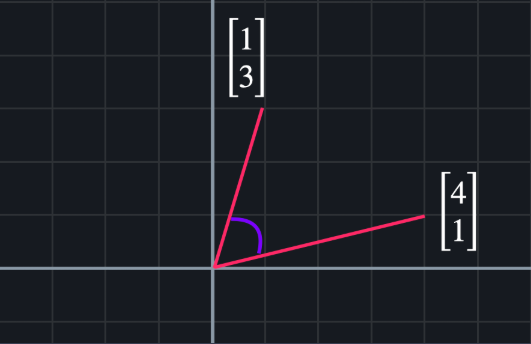
그리고 두 선 사이의 각도 $\theta$ 를 사용해서 유사도를 측정한다.
선들이 서로 반대 방향이면 각이 크기 때문에 취향이 아예 다른 유저고, 두 선이 완전히 겹치면 취향이 같은 유저이다.

이런 식으로 비슷함의 정도를 표현하며, 선들이 얼마나 긴지는 전혀 고려하지 않는다.

이렇게 해서 생긴 각도를 그대로 유사도로 쓰는 게 아니라 코사인 함수에 넣어서 $cos(\theta)$ 로 사용한다.

$cos(\theta)$ 을 구하기 앞서, 우리는 벡터의 내적을 통해 다음과 같은 공식이 나온다는 것을 알고 있다. (코사인 법칙으로 증명 가능)

\vec{a} = <a_1, a_2> , \vec{b} = <b_1, b_2>

\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 = ||\vec{a}||_{2}||\vec{b}||_{2} \cdot cos\theta

\therefore \cos\theta = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}||_{2} || \vec{b}||_{2}}

이렇게 구한 $cos(\theta)$ 값이 클수록 유사도가 큰 것이고, 작을수록 유사도가 작은 것이다.

위 사진은 두 벡터 $A$ , $B$ 의 코사인 유사도를 계산한 결과를 예시로 보여준다.

이제 코사인 유사도로 유저들간의 평점 벡터들이 서로 어느 정도 비슷한지 계산해보자.

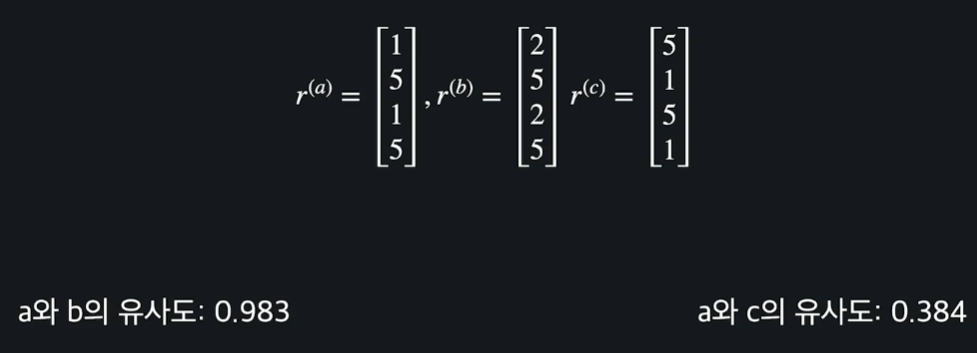
지금 보면 $a$ 와 $b$ 의 유사도는 0.983으로, $a$ 와 $c$ 의 유사도인 0.384보다 큰 것을 볼 수 있다.
따라서 $a$ 와 $b$ 가 $a$ 와 $c$ 보다 훨씬 비슷하단 걸 알 수 있다.

📍유클리드 거리 vs 코사인 유사도

유클리드 거리는 클수록 두 데이터가 다르고, 작을수록 두 데이터가 비슷하다는 의미였고, 코사인 유사도는 클수록 두 데이터가 비슷하고, 작을수록 두 데이터가 다르다는 의미였다.

또 다음과 같은 상황일 때 둘은 큰 차이를 갖는다.

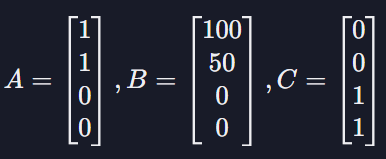
각 벡터는 유저가 특정 물품을 몇 개를 샀는지를 나타내고 있다고 하자.
(각 유저 벡터의 첫 번째 원소는 닭가슴살, 두 번째는 아령, 세 번째는 맥주, 네 번째는 피자를 몇 개를 샀는지를 나타낸다.)

직관적으로 생각해봤을 때 $A$ 와 $B$ 가 $A$ 와 $C$ 보다 훨씬 더 비슷한 구매 취향을 갖고 있는 유저인데, 유클리드 거리를 사용하면 $B$ 는 벡터가 엄청 길기 때문에 A와의 거리도 커서 서로 비슷하지 않은 유저로 계산이 된다. $A$ 와 $B$ 보다 오히려 $A$ 와 $C$ 가 훨씬 더 비슷하다고 나오는 것이다.

반면 코사인 유사도를 사용하면 $A$ 와 $B$ 는 서로 벡터의 방향이 비슷하기 때문에 $A$ 와 $B$ 가 $A$ 와 $C$ 보다 더 비슷하다고 나온다.

이는 코사인 유사도 방식에서 각 벡터, 또는 선의 크기가 중요하지 않다는 점 때문이다.

따라서 어떤 형식의 데이터를 사용하는지를 고려해서 유클리드 거리를 사용할지, 코사인 유사도를 사용할지를 잘 정해야한다.

📍데이터가 비어있는 경우

위에서 유클리드 거리와 코사인 유사도 방법을 적용할 때, 유저들의 평점 벡터에는 0인 원소가 없을 때를 가정하고 계산을 했었다.

그치만 현실 세계에서는 아래 그림과 같이 유저들이 평점을 주지 않은 영화가 충분히 있을 수 있다.

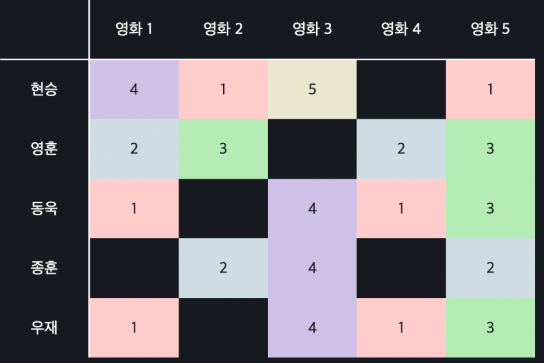
이런 경우일 때는 어떻게 계산해야 할까?

0으로 채운다
일단 가장 쉬운 방법은 비어있는 값들은 모두 0으로 생각하고 유사도를 계산하는 것이다.

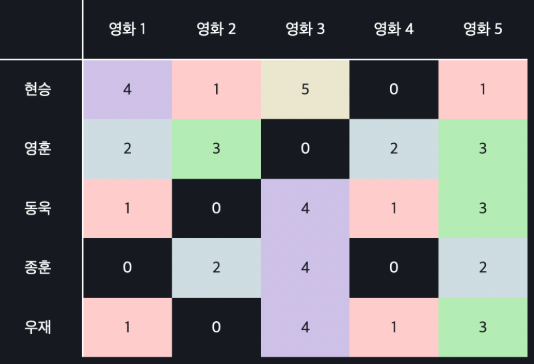
위와 같이 0으로 모두 채운 뒤, 유클리드 거리나 코사인 유사도를 계산하면 되는데 이 방법은 그리 좋지 않다.
왜냐하면 0은 최악의 평점으로도 의미가 되기 때문이다. 단순히 평점을 안 준 것일 뿐인데 유저가 싫어하는 영화로 계산이 되면 추천 시스템의 정확도가 별로 안 좋아진다.
유저 별 평균 평점으로 채운다
비어 있는 값들을 유저의 평균 평점으로 채워 넣는 방법이다.

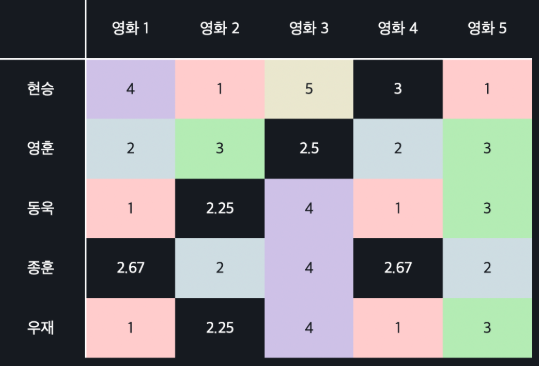
예를 들어 위의 사진과 같이 첫 번째 유저가 준 평점 평균이 3이니까 첫 번째 유저의 빈칸들을 3으로 채워 넣는 것이다.
평균은 유저가 좋아하지도, 싫어하지도 않는다고 해석될 수 있기 때문에, 모르는 평점들에 대해서 0을 사용하는 거보다 훨씬 더 합리적으로 유사도를 계산할 수 있다.
Mean Normalization를 이용하여 채운다
mean normalization은 빈칸들을 먼저 유저의 평균 평점으로 채운 뒤, 유저의 모든 평점 값들에서 평균 평점을 빼주는 방식이다. 즉, 데이터의 평균을 0으로 만들어 주는 방법이다.

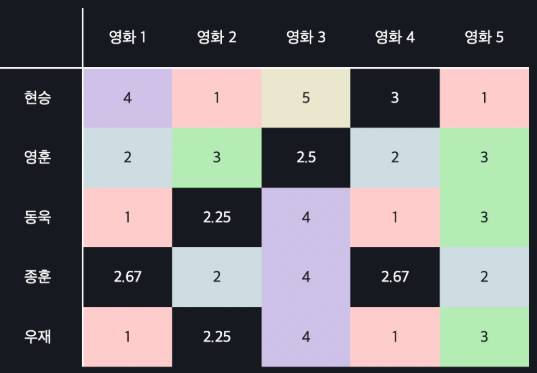
예를 들어 위와 같이 빈칸들을 먼저 유저의 평균 평점으로 채우고,

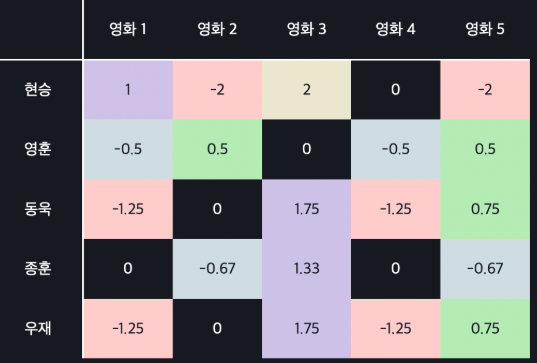
각 유저의 모든 평점 값들에서 각 유저의 평균 평점을 빼주면 되는 것이다.
mean normalization을 사용하면 까다로운 유저들과 유한 유저들에 대한 처리를 해줄 수 있다는 장점이 있다.
왜냐하면 모든 유저의 평균 평점을 0으로 맞춰주면, 유저마다의 좋고/싫고/보통인 기준들로 평가된 영화 평점들이 비슷한 값들로 바뀌기 때문에 비슷한 유저를 찾을 때 좀 더 직관적으로 찾아낼 수 있다.

📍상품 추천하기

이제 영화 평점을 예측하는 방법을 알아보자.

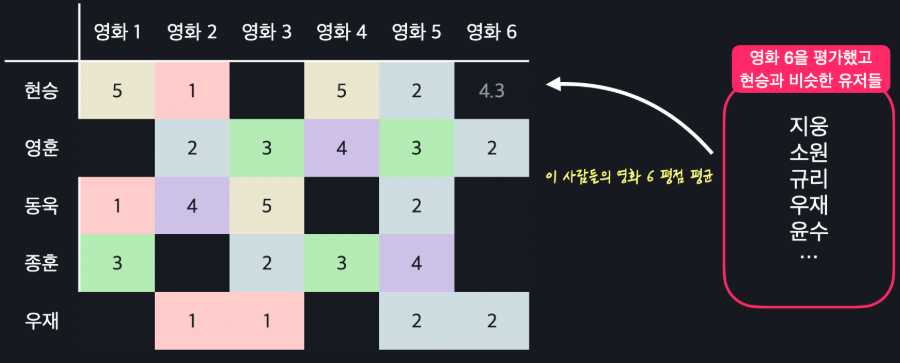
위의 사진에서처럼 평점 테이블에서 현승의 영화 6에 대한 평점을 예측하고 싶다고 하자. 그러기 위해서는 먼저 모든 유저에 대해서 현승과의 유사도를 유클리드 거리, 혹은 코사인 유사도를 통해 구한다.

그리고 그 유저들 중 영화 6에 대해 평점을 매겼고, 현승과의 유사도가 가장 높은 n명을 뽑는다. 이렇게 해서 찾은 현승과 비슷한 유저 그룹을 흔히 "이웃"이라고 부른다.

이 이웃들의 영화 6에 대한 평균 평점을 현승이가 영화 6에 대해 매길 평점이라고 예측하면 된다.

이 똑같은 과정을 다른 유저와 영화들에 대해서도 해주면 되고, 가장 예측 값이 높은 영화 k개를 각 유저에게 추천하면 되는 것이다.

이를 수학식으로 한 번 표현하면 다음과 같다.

r^{(x)}_i = \frac{1}{k}\sum_{y\in N}r^{(y)}_i

$r^{(x)}_i$ : 유저 $x$ 의 영화 $i$ 에 대한 평점
$N$ : 유저의 이웃 (상품 $i$ 를 평가한 유저 중, 유저 $x$ 와 가장 비슷한 $k$ 명의 집합)

따라서 수학식은 이웃 $N$ 에 속한 모든 유저들 $y$ 에 대해서, 그 유저들의 영화 $i$ 에 대한 평점을 다 더해준 뒤 이웃의 수 $k$ 로 나눠준 것이다.

쉽게 말해 $k$ 명의 이웃들의 영화 $i$ 에 대한 평점을 평균 낸 것이고, 이게 바로 유저 $x$ 의 영화 $i$ 에 대한 예측값인 것이다.

이 식을 사용해서 평점 테이블의 빈 원소들을 채운 후, 예상 평점이 가장 높은 영화 몇 개를 유저에게 추천해 주면 되는 것이다.

이러한 방식은 유저 기반 헙업 필터링이라고 하는데, 상품 기반 협업 필터링은 어떻게 다른지 알아보자.

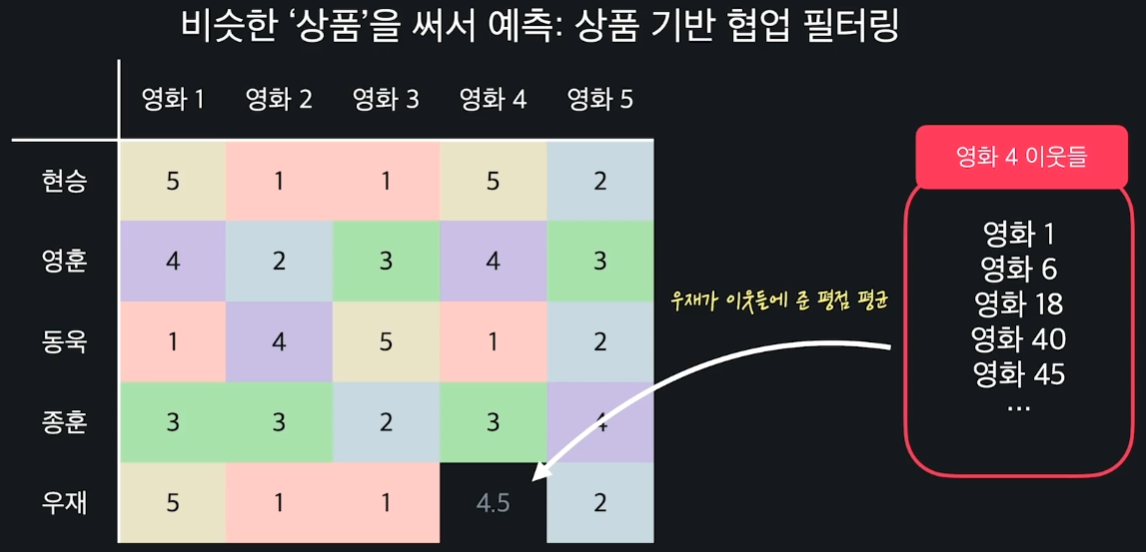
우재의 영화 4에 대한 평점을 예측해본다고 하자. 유저 기반이 아닌 상품 기반이기 때문에 영화 4와 유사한 이웃들을 찾아야 한다.

이때도 유클리드 거리 방식이나 코사인 유사도 방식을 적용할 수 있다. 영화 4와 유사한 이웃들 n개를 뽑고, 이 이웃들 중에서 유저 우재가 매긴 평점들의 평균값을 계산한다.

이 값이 우재의 영화 4에 대한 예측 평점이 되는 것이다.

이론상으로 유저 기반 협업 필터링과 상품 기반 협업 필터링은 큰 차이가 없지만, 실전에서는 유저들이 상품보다 더 복잡하기 때문에 상품 기반 협업 필터링이 더 성능이 좋은 경우가 많다.

상품 기반 협업 필터링일 때의 수학식은 아래와 같다.

r^{(x)}_i = \frac{1}{k}\sum_{j\in N}r^{(x)}_j

$r^{(x)}_i$ : 유저 $x$ 의 영화 $i$ 에 대한 평점
$N$ : 영화의 이웃 (유저 $x$ 가 평가한 영화 중, 영화 $i$ 와 가장 비슷한 영화 $k$ 개의 집합)

따라서 수학식은 이웃 $N$ 에 속한 모든 영화들 $j$ 에 대하여, 유저 $x$ 의 영화 $j$ 에 대한 평점을 전부 더한 뒤, 이웃의 수 $k$ 로 나눠준 것이다.

쉽게 말하면 유저 $x$ 가 평가한 $k$ 개의 이웃들의 평점을 평균 낸 것이고, 이게 바로 유저 $x$ 의 영화 $i$ 에 대한 예측값인 것이다.

유저 기반 협업 필터링을 할 때랑 똑같이 이 식을 사용해서, 평점 데이터의 빈 원소들을 채운 후 예상 평점이 가장 높은 영화 몇 개를 유저에게 추천해 주면 된다.

📍협업 필터링 장단점

장점

속성을 찾거나 정할 필요가 없다
좀 더 폭넓은 상품을 추천할 수 있다
내용 기반 추천보다 성능이 더 좋게 나오는 경우가 많다

단점

데이터가 많아야 한다
인기가 많은 소수의 상품이 추천 시스템을 장악할 수 있다
어떤 상품이 왜 추천됐는지 정확히 알기 힘들다

이러한 장단점은 뭔가 내용 기반 추천 방식과 상반되는 장단점을 많이 갖고 있는 것처럼 보인다.

그렇다면 실제로 추천할 때는 어떤 방식을 사용해야 할까?

실제로는 앙상블 방식으로, 추천할 상품 12개 중 3개는 선형 회귀, 3개는 다항 회귀, 3개는 유저 기반 협업 필터링, 나머지 3개는 상품 기반 협업 필터링으로 추천을 할 수 있다.

또, 이러한 각기 다른 방법들로 전부 평점을 예측해보고 이 값들의 평균을 이용하는 방법도 있을 수 있다.

이처럼 여러 방식을 합쳐서 사용하면 모델들의 단점을 보완하면서 장점을 살릴 수 있다.

출처: 코드잇

wnsdnl

이전 포스트

ML_Bagging, Boosting

다음 포스트