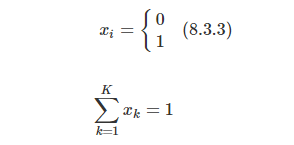📌확률론 맛보기
✍딥러닝에서 확률론이 왜 필요한가요?
-
딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있습니다.
-
기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하게 됩니다.
- 예측이 틀릴 위험(risk)을 최소화하도록 데이터를 학습하는 원리는 통계적 기계학습의 기본 원리이다.
-
회귀 분석에서 손실함수로 사용되는 L2-norm은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도합니다.
-
분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도합니다.
-
즉, 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야 합니다.
오늘 학습한 내용을 정리하기 전에 헷갈리던 중요한 몇몇 개념들을 간단하게 학습해보겠습니다.
📒확률통계 개념 정리
-
모집단 : 연구자가 알고 싶어하는 대상 / 집단 전체
-
표본 (Sample) : 연구자가 측정 또는 관찰한 결과들의 집합
-
표본 공간 (sample space) : 어떤 특정 실험 또는 무작위 실험을 했을 때, 측정가능한 모든 결과들의 집합. 표본(sample)은 표본 공간의 부분집합이라고 할 수 있다.
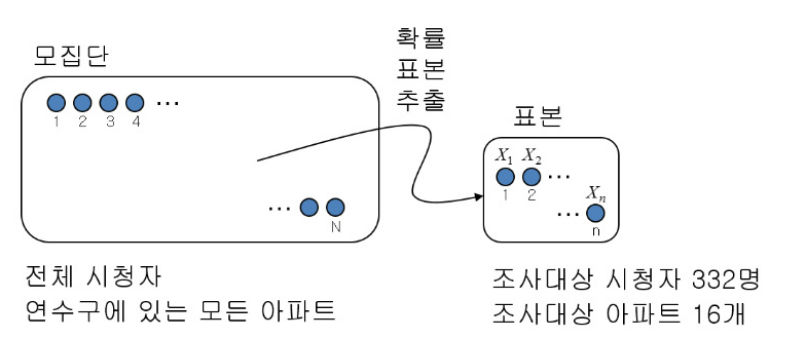
- ex) 동전을 반복해서 두 번 던지는 실험을 한다고 하면, 표본 공간(S)는 다음 그림과 같습니다.
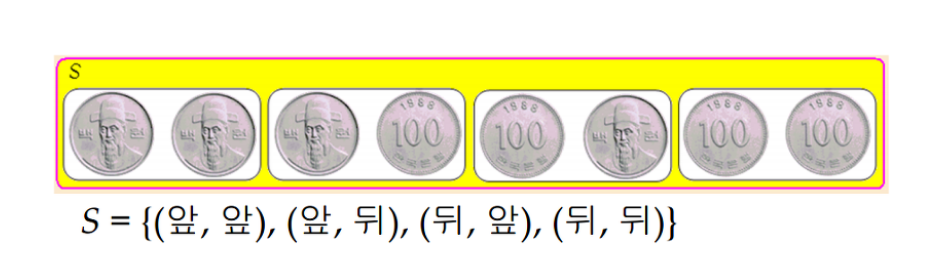
- ex) 동전을 반복해서 두 번 던지는 실험을 한다고 하면, 표본 공간(S)는 다음 그림과 같습니다.
-
사건(event) : 표본공간의 부분집합으로 어떤 조건을 만족하는 특정한 표본들의 집합.
-
확률(probability) : 동일한 조건 하에서 동일한 실험을 무수히 많이 반복하여 실시할 때, 어떤 특정한 사건이 발생하는 비율
-
확률변수(random variable) : 무작위 실험을 했을 때, 특정 확률로 발생하는 각각의 결과를 수치적 값으로 표현하는 변수. "이산확률변수"와 "연속확률변수"가 있다.
- ex) 동전을 무작위로 두 번 던져서 그림 또는 숫자가 나오는 실험에서 일정한 확률(앞이 나올 확률 1/2, 뒤가 나올 확률 1/2)을 가지고 발생하는 결과에 실수 값(앞=1, 뒤=0)을 부여하는 변수
-
확률 분포(Probability distribution) : 확률 변수가 특정한 값을 가질 확률을 나타내는 함수. 즉, 확률분포란 확률변수가 특정 값을 가질 확률이 얼마나 되느냐를 나타낸다.
✍이산확률변수 VS 연속확률변수
-
확률변수는 확률분포 D에 따라 이산형(discrete)와 연속형(continuous)확률변수로 구분하게 됩니다.
-
이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링합니다. 이산형 확률변수를 확률질량함수(probability mass function)라고 부르기도 합니다.
-
연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링합니다. 확률밀도함수(probability density function)라고 부르기도 합니다.
- 밀도는 누적확률분포의 변화율을 모델링하며 확률로 해석하면 안됩니다.
✍확률분포는 데이터의 초상화
-
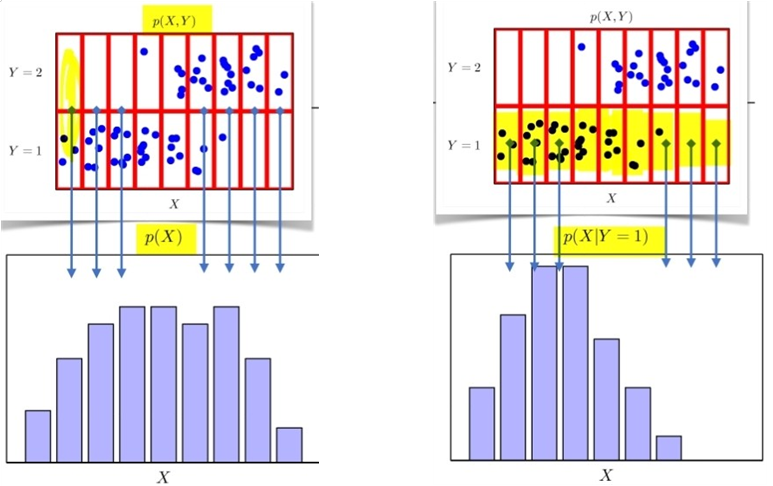
데이터공간을 라 표기하고, 확률분포 D는 데이터공간에서 데이터를 추출하는 분포입니다.
-
결합분포 는 확률분포 D를 모델링합니다.
-
는 입력 에 대한 주변확률분포로 에 대한 정보를 주진 않습니다.
-
주변확률분포 는 결합분포에서 유도 가능합니다.
-
-
-
조건부확률분포 는 데이터 공간에서 입력 와 출력 사이의 관계를 모델링합니다.
아래 그림은 주어진 데이터에 대한 주변확률분포 와 조건부확률분포 를 시각화 한 그림입니다.
✍조건부확률과 기계학습
-
조건부확률 는 입력변수 에 대해 정답이 일 확률을 의미합니다.
-
로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됩니다.
-
분류 문제에서 는 데이터 로부터 추출된 특징패턴 와 가중치행렬 를 통해 조건부확률 를 계산합니다.
-
회귀 문제의 경우 조건부기대값 을 추정합니다.
-
-
조건부기대값은 을 최소화하는 함수 와 일치하기 때문에, 회귀 문제에서 많이 사용합니다.
-
물론 원하는 목적에 따라 조건부기대값 뿐만 아니라 다른 예측 통계량을 사용할 수 있습니다.
-
-
딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 를 추출합니다.
- 특징패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습 문제와 모델에 의해 결정됩니다.
- 특징패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습 문제와 모델에 의해 결정됩니다.
✍기대값이 뭔가요?
-
확률분포가 주어지면 데이터를 분석하는 데 사용 가능한 여러 종류의 통계적 범함수(statistical functional)를 계산할 수 있습니다.
-
기대값(expectation)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용됩니다.
-
기대값을 이용해 분산, 첨도, 공분산 등 여러 통계량을 계산할 수 있습니다.
✍몬테카를로 샘플링
-
기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분입니다.
-
확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 합니다.
-
몬테카를로는 이산형이든 연속형이든 상관없이 성립합니다.
-
또한 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장합니다.
-
아이디어는 합 또는 적분을 일부 분포에서 기대치인 것처럼 보고 해당 평균으로 기대치를 근사화하는 것입니다.
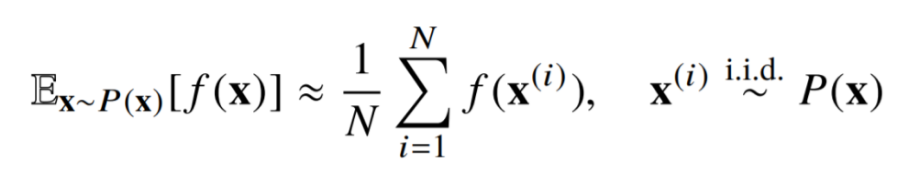
👉 데이터 공간 에서 i.i.d(independent and identically distribute), 즉 확률변수 가 상호독립적이면서 모두 동일한 확률분포를 가진다면, 기대값은 랜덤하게 뽑은 N개 샘플의 평균치로 나타낼 수 있습니다. -
쉽게 이해하기 위해 위키피디아에 있는 예시를 보겠습니다. 단위 정사각형에 새겨진 사분원을 생각했을때, 몬테카를로 방법을 사용하면 의 값을 근사치로 추정할 수 있습니다.
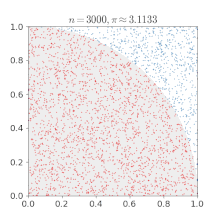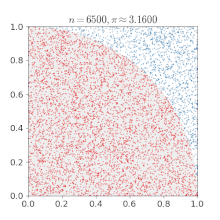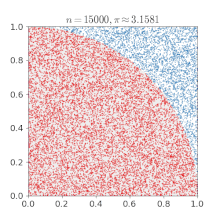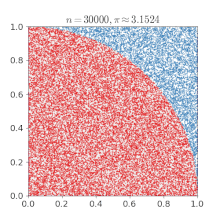
- 정사각형을 그린 다음, 그 안에 사분원을 삽입한다.
- 정사각형 위에 일정한 개수의 점을 균일하게 분포한다.
- 사분원 내부의 점(즉, 원점으로부터 1 미만)의 개수를 센다.
- 내부의 개수와 전체 개수의 비율은 두 영역의 비율을 나타낸다. 그 값에 4를 곱하여 를 만든다. 왜냐하면 원에 속한 점 개수를 전체 점 개수로 나눈 비율이 에 근사하기 때문이다.
📌통계학 맛보기
✍모수가 뭐에요?
-
모수(parameter)란 "모집단의 특성을 나타내는 수치"입니다.
-
통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표입니다.
-
그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정할 수 밖에 없습니다.
-
데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라 합니다.
-
특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric)방법론 이라 부릅니다. 특히 기계학습의 많은 방법론이 비모수 방법론에 속합니다.
✍확률분포 가정하기:예제
-
확률분포를 가정하는 방법 : 우선 히스토그램을 통해 모양을 관찰합니다.
- 데이터가 2개의 값(0 또는 1)만 가지는 경우 -> 베르누이분포
- 데이터가 n개의 이산적인 값을 가지는 경우 -> 카테고리분포, 다항분포
- 데이터가 [0,1] 사이에서 값을 가지는 경우 -> 베타분포
- 데이터가 0 이상의 값을 가지는 경우 -> 감마분포, 로그정규분포 등
- 데이터가 실수 전체에서 값을 가지는 경우 -> 정규분포, 라플라스분포 등
-
기계적으로 확률분포를 가정해서는 안 되며, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙입니다.
✍데이터로 모수를 추정해보자
- 데이터의 확률분포를 가정했다면 모수를 추정해볼 수 있습니다.
모수가 모집단 분포 특성을 설명하는 값인 것 처럼, 확률표본(모집단을 구성하고 있는 데이터에서 랜덤하게 추출한 표본)의 특성을 설명하는 값이 존재합니다. 이것을 통계량(statistic)이라 부르며, 통계량에는 표본평균, 표본분산, 표본표준편차, 표본비율, 표본상관관계 등이 있습니다.
그렇다면 모수와 통계량은 무엇이 다른가? 모수는 모집단이 변하지 않기 때문에 그 값이 변하지 않지만, 통계량은 표본을 어떻게 추출하느냐에 따라서 그 값이 다르게 나타납니다.
즉, 동일한 모집단에서 동일한 수의 표본을 추출하더라도 매번 표본이 달라지기 때문에 각 표본의 통계량은 서로 다르게 나타날 수 있습니다.
✎ "통계량은 표본을 추출할 때마다 매번 달라지는데 어떻게 매번 변하는 통계량을 가지고 모수를 추정하나요?"
👉 예를 들어 모수를 추정하기 위해 30개씩 n번 표본(sample)을 무작위로 추출했다고 가정해보면, 표본평균은 우리가 추출한 표본(sample)에 따라 그 값이 변화합니다. 여기서 중요한 것은 표본평균은 표본(sample)이 어떻게 추출되느냐에 따라 특정 확률로 변화하므로 표본평균(통계량)은 확률변수라고 할 수 있습니다. 그리고 n번 반복 추출된 표본들 각각의 평균값들은 확률 변수이기 때문에 그에 대응하는 확률값들이 있습니다. 그 확률값들의 분포를 계산하면 표본평균들의 확률분포를 그릴 수 있습니다. 이것을 통계량의 확률분포라고 할 수 있고, 이를 표집분포(sampling distribution)라고 부릅니다
그렇다면 표본분포(sample distribution)와 표집분포(sampling distribution)은 뭐가 다른가?
표본 분포(sample distribution)는 모집단에서 추출한 하나의 샘플의 분포를 말하는 것
표집 분포(sampling distribution)는 여러 개 샘플들을 뽑아, 각 샘플의 평균에 대한 분포를 그린 것
-
정규분포의 모수는 평균 과 분산 으로, 이를 추정하는 통계량(statistic)은 다음과 같습니다.

- 표본분산의 분모가 N이 아닌 N-1이 됩니다. 이것을 베셀 보정(Bessel’s Correction)이라고 하는데, 샘플링한 표본들은 평균적으로 모집단 기댓값보다는 표본 기댓값에 더 가깝게 형성되어 있기 때문에 표본 분산 값은 모집단 분산 값보다 낮게 측정됩니다. 그거를 약간 조정하기 위해 N-1을 이용하여 표본 분산 값을 톡 쳐서 올려준다는 논리입니다.
-
통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포, 즉 표본평균분포는 N이 커질수록 정규분포를 따릅니다.
- 이를 중심극한정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립합니다.
- 이를 중심극한정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립합니다.
✍최대가능도 추정법
확률과 우도(가능도)에 대한 개념이 헷갈리기 때문에 개념을 잡고 가겠습니다.
확률(Probability) : 확률은 관측값 또는 관측 구간이 주어진 확률분포 안에서 얼마만큼 나타날 수 있는가에 대한 값입니다. 즉, 고정된 모수에 대해 확률을 얻는 것.
우도(가능도,Likelihood) : 우도는 연속형 확률변수에서의 확률과는 개념적으로 반대되는 지표라 할 수 있습니다. 가능도란 어떤 특정한 값을 관측할 때, 이 관측치가 어떠한 확률분포에서 나왔는가에 관한 값입니다. 즉, 주어진 관측값으로부터 데이터를 잘 표현하는 모수를 얻는 것.
-
표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 됩니다.
-
이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(MLE)입니다.

-
데이터 집합 가 독립적으로 추출되었을 경우 로그가능도를 아래 그림과 같이 확률밀도함수의 곱으로 표현할 수 있습니다. 이 경우에는 로그함수를 취해줘서 오른쪽 식과 같이 로그 확률분포들의 덧셈으로 바꿀 수 있게 됩니다.
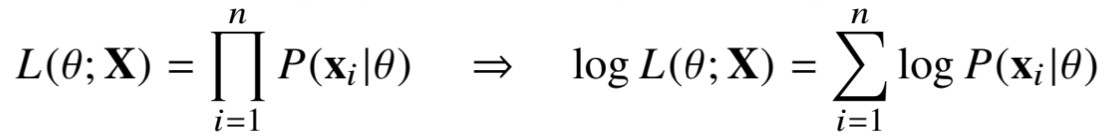
✍왜 로그가능도를 사용하나요?
-
로그가능도를 최적화하는 모수 는 가능도를 최적화하는 MLE가 됩니다.
-
데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가능합니다.
-
데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해집니다.
-
경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그 가능도를 사용하면 연산량을 에서 으로 줄여줍니다.
-
대게의 손실함수의 경우 경사라강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화하게 됩니다.
✍최대가능도 추정법 예제: 정규분포
- 정규분포를 따르는 확률변수 로부터 독립적인 표본 을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
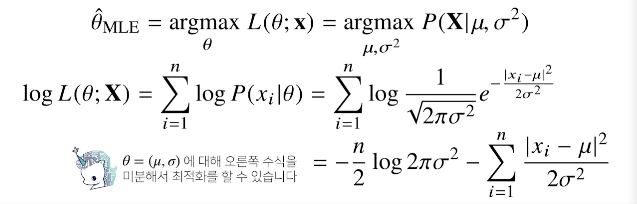
정규분포는 평균과 분산이라는 모수를 가지고 있기 때문에 대신 으로 쓸 수 있습니다. 이를 가지고 로그우도를 계산해 보면 위 그림과 같습니다.
주어진 로그우도를 와 에 대해서 각각 편미분을 해주면 아래 그림과 같이 두 개의 식을 얻을 수 있습니다. 두 미분이 모두 0이 되는 와 를 찾으면 우도를 최대화하게 됩니다.
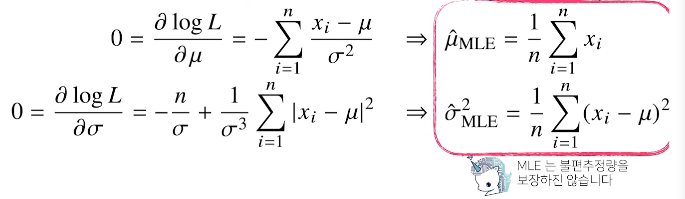
✍최대가능도 추정법 예제: 카테고리 분포
카테고리 확률변수는 1부터 K까지의 K개의 정수값 중 하나가 나옵니다.
ex) 주사위를 던져 나오는 눈금의 수는 K=6 인 카테고리 분포가 됩니다.주의할 점은 원래 카테고리는 스칼라 값이지만 카테고리 확률변수는 아래 그림과 같이 0과 1로만 이루어진 다차원 벡터를 출력합니다.
위 그림과 같이 숫자를 변형하는 것을 원핫인코딩이라고 합니다. 따라서 확률변수의 값도 처럼 벡터로 표시합니다. 이 벡터를 구성하는 원소는 다음과 같은 제한 조건이 있습니다.
원솟값 는 베르누이 확률변수로 볼 수 있기 때문에 각각 1이 나올 확률을 나타내는 모수 를 가집니다. 따라서 전체 카테고리분포의 모수는 처럼 벡터로 나타낼 수 있고, 다음과 같은 제한 조건을 가집니다.
- 카테고리 분포 Multinoulli를 따르는 확률변수 로부터 독립적인 표본 을 얻었을 때 최대가능도 추정법을 이용하여 모수를 측정하면?
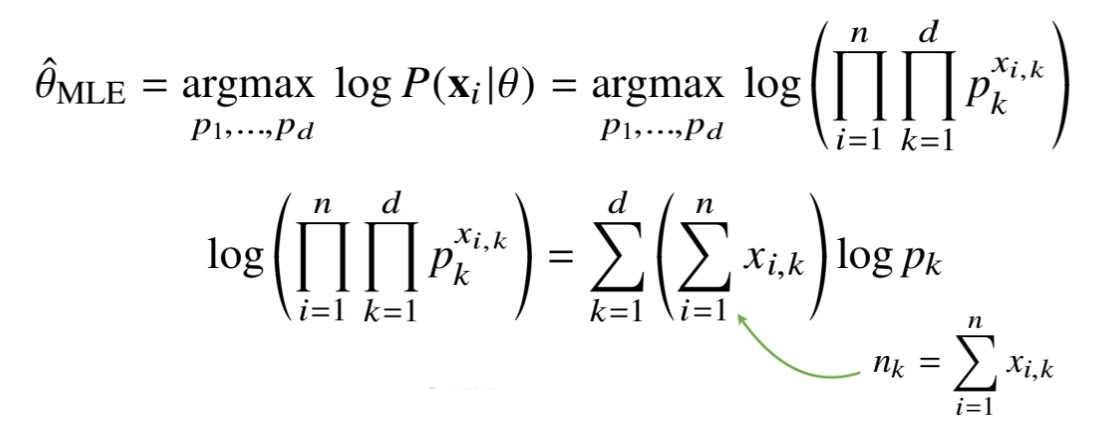
먼저 카테고리 분포의 우도함수를 표현할 때 위 그림처럼 모수 에 해당하는 값에 주어진 데이터 에 해당하는 값을 승수로 취해줍니다.
위 그림의 product 식을 풀어쓰면 두 번째 식으로 나타낼 수 있는데, 이때 는 주어진 각 데이터들에 대해서 k값이 1인 개수를 세는 값으로 대체해서 표현할 수 있습니다. 정리하면 다음 그림과 같이 식을 나타낼 수 있습니다.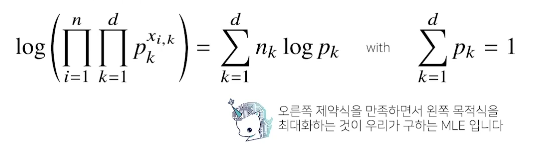
저희는 위 그림의 오른쪽 제약식을 만족하면서 왼쪽의 목적식을 최대화 해야합니다.
이는 라그랑주 승수법통해 최적화를 할 수 있습니다. 아래 그림과 같이 제약식을 우변으로 옮겨준 상태에서 를 곱해준 식을 원래 목적식에 더해줌으로써 새로운 목적식을 만들어 줍니다.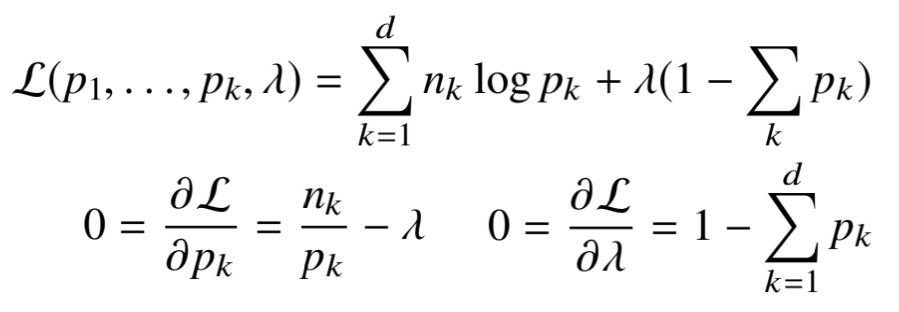
이후 주어진 식을 와 로 편미분해서 나온 식이 0이 되는 에 대해서 나타내면 다음과 같습니다.
✍딥러닝에서 최대가능도 추정법
-
최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있습니다.
-
딥러닝 모델의 가중치를 라 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수 를 모델링합니다.
-
원핫벡터로 표현한 정답레이블 을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그우도를 최적화할 수 있습니다.
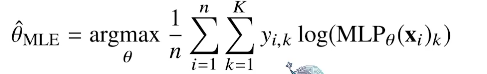
이번에 AI Math 강의를 들으면서 선형대수 및 확률론과 통계론이 너무 어려웠습니다..
따로 선형대수화 확률론은 필수로 따로 공부를 해야할 것 같습니다. ㅠ