📌베이즈 통계학 맛보기

✍조건부확률이란?

• 베이즈 통계학을 이해하기 위해선 조건부확률의 개념을 이해해야 합니다.

  $P(A\cap B)=P(B)P(A|B)$
  
  조건부확률 $P(A|B)$는 사건 B가 일어난 상황에서 사건 A가 발생할 확률을 의미합니다.

• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려줍니다.

  $P(B|A)=\frac{P(A \cap B)}{P(A)} = P(B)\frac{P(A|B)}{P(A)}$

✍베이즈 정리: 예제

• 베이즈 정리 $\to$ $P(\theta | D) = P(\theta)\frac{P(D|\theta)}{P(D)}$

D 는 관찰하는 데이터이고 $\theta$는 모수(parameter) 입니다.

• $P(\theta | D)$ : 사후확률(posterior), 데이터를 관찰했을 때 파라미터가 성립할 확률
• $P(\theta)$ : 사전확률(prior), 데이터를 분석하기 전에 파라미터에 대한 확률
• $P(D|\theta)$ : 우도(likelihood)
• $P(D)$ : evidence, 데이터 자체의 분포

• COVID-99 의 발병률이 10% 로 알려져있다. COVID-99에 실제로 걸렸을때 검진될 확률은 99% , 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률 은?
  $\Rightarrow$ 먼저 $\theta$ 를 COVID-99 발병 사건으로 정의(관찰불가)하고, D를 테스트 결과라고 정의(관찰가능)합니다. 그러면 사전확률 은 발병률이므로 $P(\theta) = 0.1$ 이고, 우도(likelyhood) 는 실제로 걸렸을때 검진될 확률인 0.99와 실제로 걸리지 않았는데 걸렸다고 나올 확률인 0.01입니다.
  즉, $P(D|\theta)=0.99, \; P(D|\theta^c)=0.01$ 입니다. 베이즈 정리를 사용하기 위해서 저희는 evidence인 $P(D)$ 를 알아야 합니다. 이는 주변확률 계산 공식을 사용하면 다음과 같이 나타낼 수 있습니다.
  
  $P(D) = \sum_\theta{P(D|\theta)P(\theta)}=P(D|\theta)P(\theta)+P(D|\theta^c)P(\theta^c)=0.108$
  
  그러므로 저희가 알고싶은 사후확률 $P(\theta|D)=0.1\times\frac{0.99}{0.108} \approx 0.916$ 입니다.
  
  만약 오검진될 확률이 1%가 아닌 10%면 어떻게 될까요?
  $P(D|\theta^c)=0.1$ 이므로 $P(D)=0.189$ 가 되고, 사후확률 $P(\theta|D)=0.1\times\frac{0.99}{0.189}\approx0.524$ 가 되어, 이전의 사후 확률과 비교했을때 거의 절반 가까의 감소했습니다.
  
  나중에 얘기하겠지만 오탐률(False alarm)이 오르면 테스트의 정밀도(Precision)가 떨어지는 예를 잘 보여주는 예제였습니다.
  
  

✍조건부 확률의 시각화(confusion matrix)

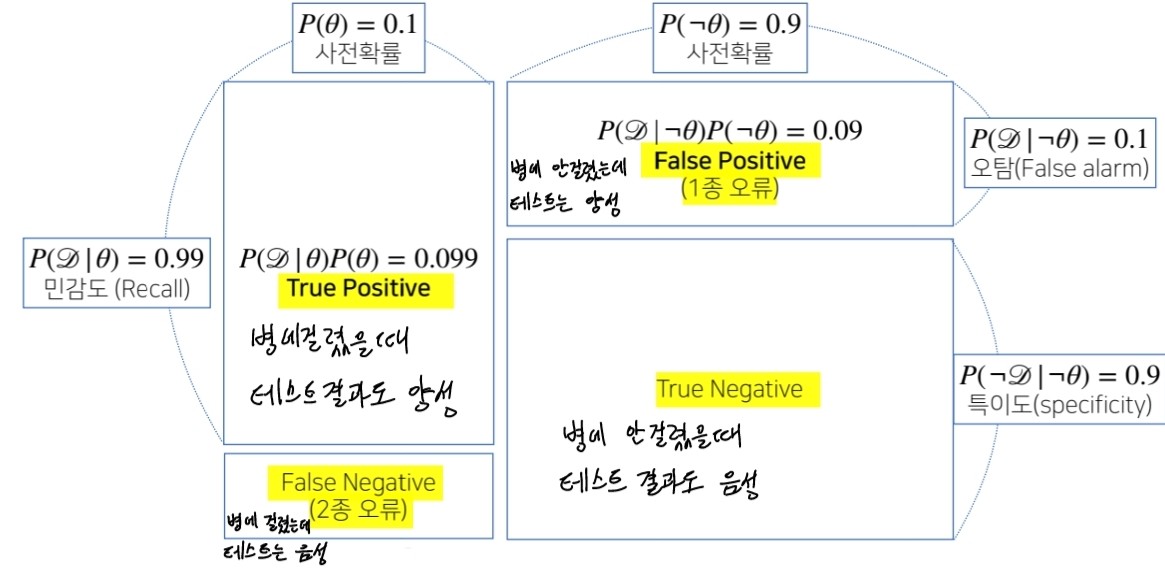
• 정확도(Accuracy) = $\frac{TP+TN}{TP+TN+FP+FN}$
  모든 분류 결과중에서 실제 참:예측 참, 실제 거짓:예측 거짓의 비율

• 정밀도(Precision) = $\frac{TP}{TP+FP}$ ,
  모델이 참으로 분류한 결과 중에서 실제 참의 비율. 얼마나 정밀하게 참으로 분류했는지를 표현.

• 재현도(Recall) = $\frac{TP}{TP+FN}$
  정밀도와 비교되는 척도로서, 실제 참 중에서 모델이 참으로 분류한 비율.
  정밀도는 모델이 참으로 분류한 것이 기준인 반면, 재현도는 실제 참값이 기준

• F1 score = $2\times\frac{Precision*Recall}{Precision+Recall}$
  Precision과 Recall의 조화평균.
  
  

✍베이즈 정리를 통한 정보의 개신

• 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률 을 계산할 수 있습니다.
  
• 앞서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때 진짜 COVID-99 에 걸렸을 확률은?
  
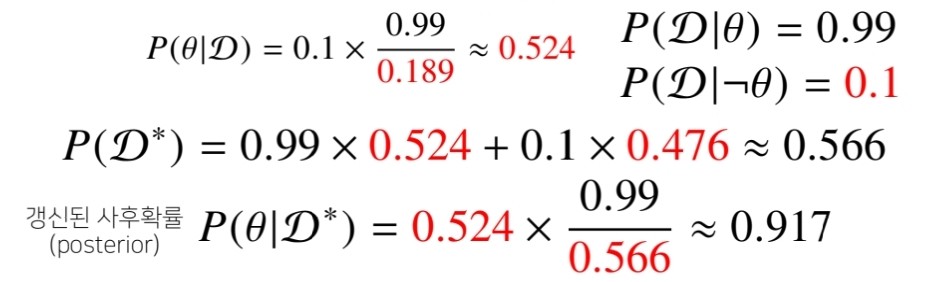
  위 그림을 보시면 이전에 계산했던 사후확률 $P(\theta|D)$를 두 번째 검진시 사전확률로 사용하여 새로운 evidence $P(D^* )$ 를 구해줍니다. 이후 갱신된 사후확률도 마저 구해주면, 이전 사후확률 값임 0.524보다 훨씬 증가한 0.917을 구할 수 있습니다.
  
  

✍조건부 확률 $\to$ 인과관계?

• 조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계(causality)를 추론할 때 함부로 사용해서는 안 됩니다.

• 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요합니다.

• 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거 하고 원인에 해당하는 변수만의 인과관계를 계산해야 합니다.

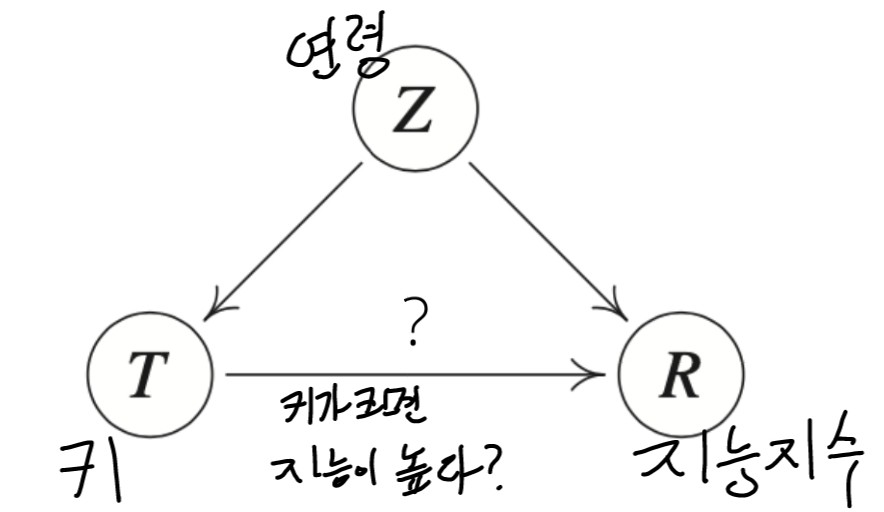
  • ex) 키(T)가 크면 지능지수(R)가 높은지를 예측하는 모델을 만들고자 할때, 원래 키와 지능지수는 연관이 없기 때문에 예측을 제대로 할 수 없습니다. 하지만 연령(Z)이라는 중첩요인을 제거하지 않으면 "키가 크면 연령이 높기 때문에 지능이 높다" 라고 해석할 수 있어서, 데이터 분석시 "키가 크면 지능지수가 높다"라고 예측을 하게 됩니다.
    
    
    

  ---