📌CNN 첫걸음

✍Convolution 연산 이해하기

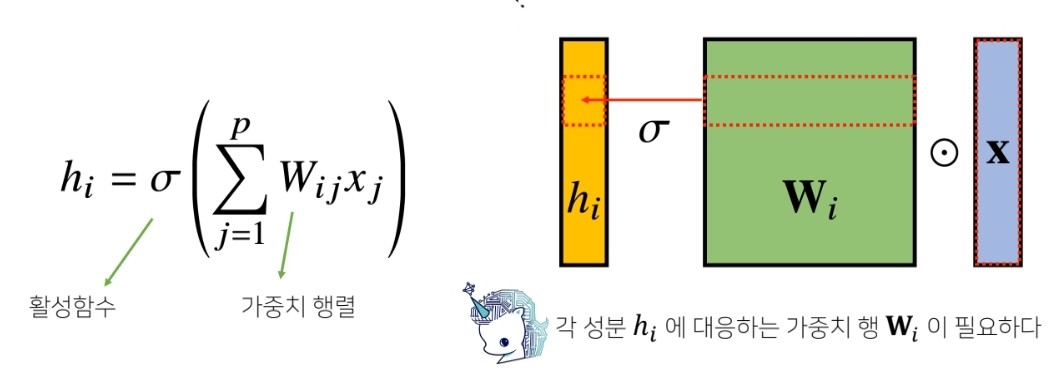
• 지금까지 배운 다층신경망(MLP)은 각 뉴런들이 선형모델과 활성함수로 모두 연결된 FC (Fully connected) 구조였습니다. MLP는 i가 바뀌면 사용되는 가중치도 바뀝니다.
  

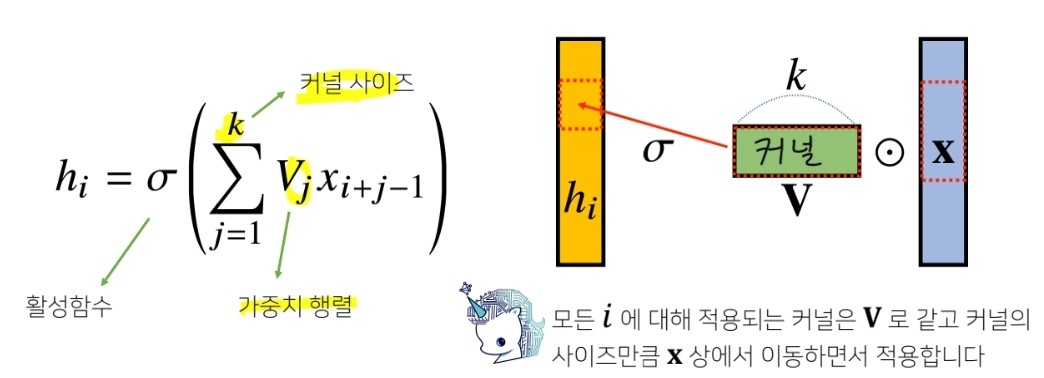
• Convolution 연산은 이와 달리 커널(kernel) 을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.
  

• 사실 Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링 하는 것입니다.
  
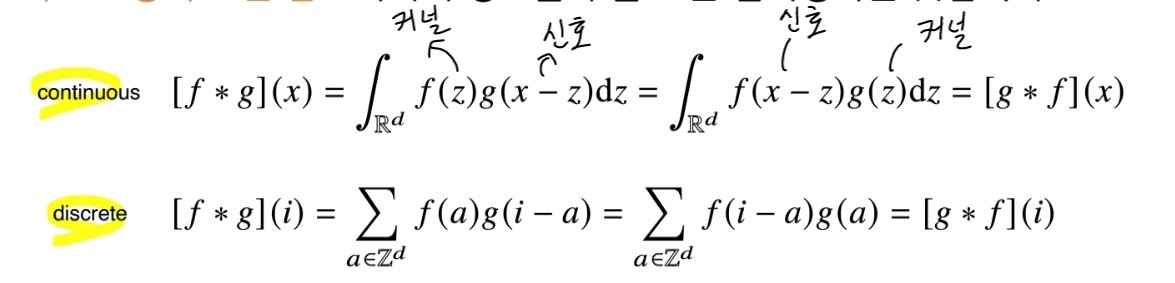
  하지만 아래 그림에서 보시다 시피 CNN에서 사용하는 연산은 사실 convolution 이 아니고 cross-correlation이라 부릅니다. 그렇다면 왜 cross-correlation이 아니라 convolution 연산이라 부를까? 이것은 오래전부터 관용적으로 convolution이라 불렀기 때문에 라고 합니다.
  

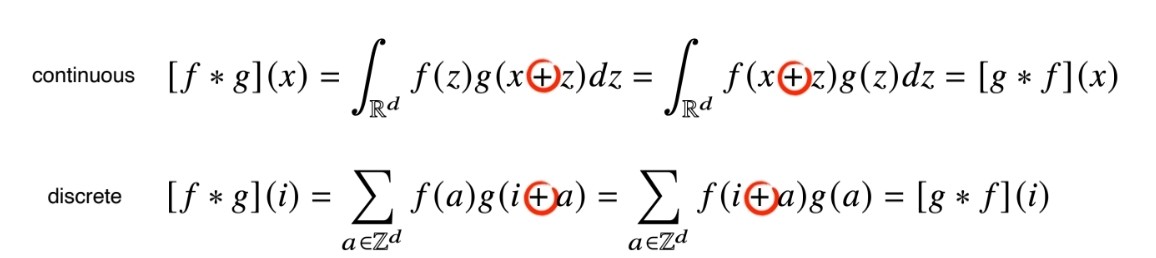
• Convolution 연산은 1차원뿐만 아니라 다양한 차원에서 계산이 가능합니다.
  

• 즉, CNN은 convolution 연산을 이용한 부분연결 구조로 FC 구조에 비해 복잡도를 크게 낮춘 구조입니다.
  더 깊게 들어가면 CNN은 conv층과 pooling층과 Fc층으로 이루어져 있는데, Convolution층에서는 학습에 의해 결정된 봇구의 커널들에 대응되는 특징들을 추출합니다. 또한 각 커널은 매개변수를 공유함으로써 FC 구조 대비 학습 매개변수가 매우 적습니다.
  Pooling층은 추출된 영상의 특징을 요약하고 강화하는 층입니다.
  
  

✍2차원 Convolution 연산 이해하기

• 2D-conv 연산은 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다. 아래 그림을 보시면 이해하기가 더 쉽습니다.
  
  
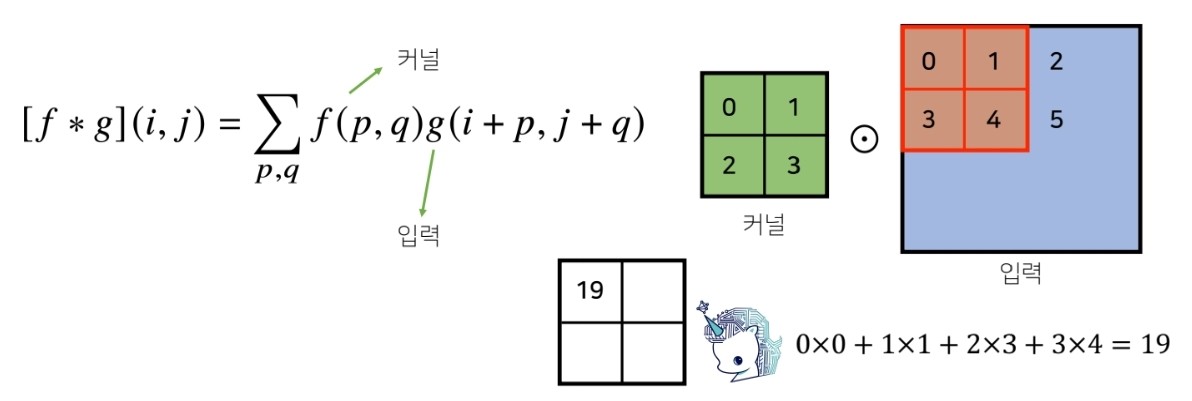
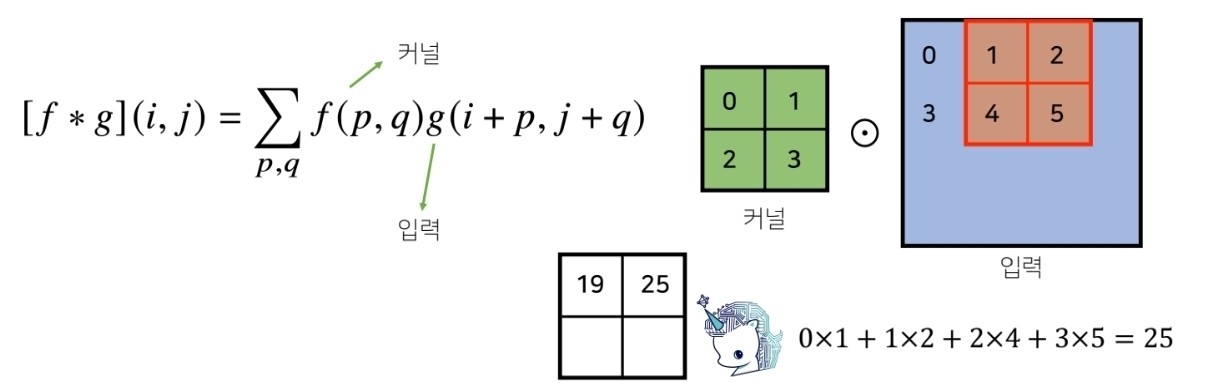
  위 그림과 같이 커널이 2D데이터를 슬라이싱 하면서 convolution 연산을 수행합니다.
  convolution 연산을 수행하여 출력되는 것을 특징맵이라고 부릅니다.
  convolution 연산의 출력인 특징맵의 크기는 다음과 같이 계산합니다.

  입력 크기 : $(H,W)$, 커널 크기 : $(K_H,K_W)$, 출력 크기 : $(O_H,O_W)$ 패딩 : P, 보폭 : S

  $O_H = \frac{H - K_H + 2P}{S}+1$

  $O_W = \frac{W - K_W + 2P}{S}+1$

• 보통 이미지는 RGB채널을 포함한 3차원 텐서입니다. 이와같이 채널이 여러개인 2차원 입력의 경우 커널을 채널 개수만큼 적용한다고 생각하시면 됩니다. 즉, 채널이 여러개인 경우 커널의 채널수는 입력의 채널수와 같아야 합니다.
  
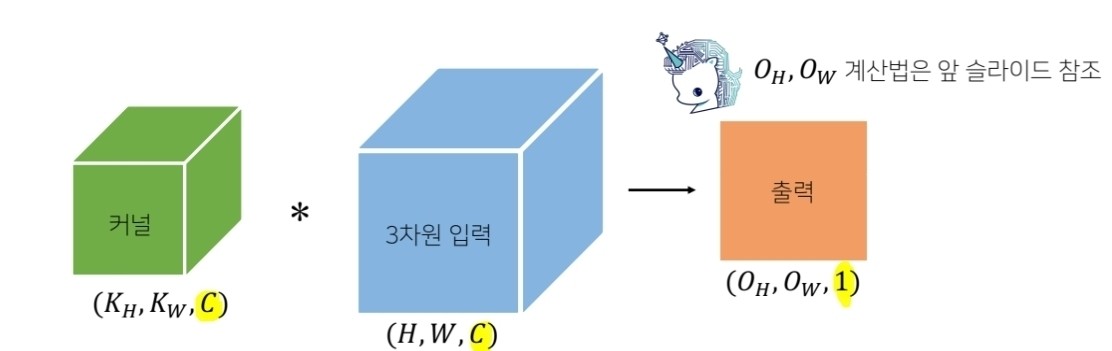
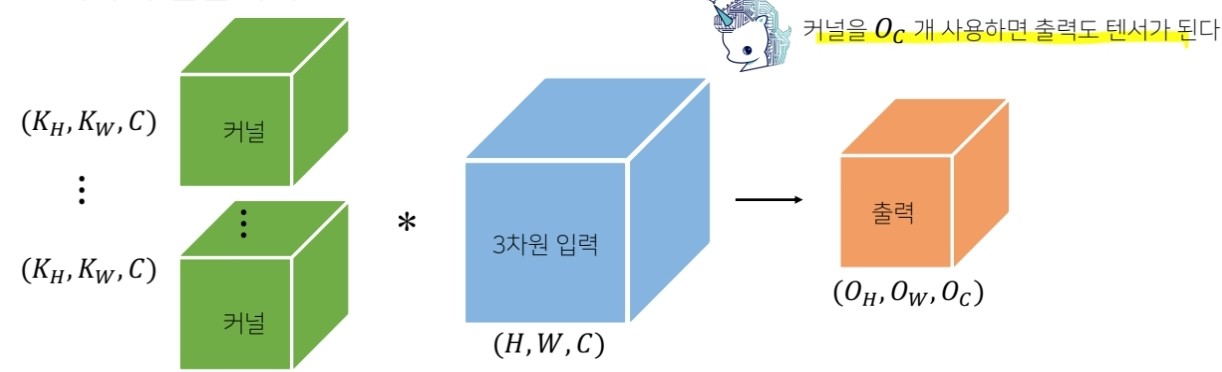
  위 그림을 보시면 채널이 여러개인 2차원 입력의 채널과 커널의 채널 수가 같으면 특징맵은 1개가 출력됩니다. 또한, 만약 커널을 여러 개를 사용하면 특징맵의 채널수는 사용한 커널의 개수가 됩니다.
  
  

✍Convolution 연산의 역전파 이해하기

• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.
  
  
  
  그림을 통해 이해를 해보겠습니다. 아래 그림을 보시면 입력벡터 X와 커널W 출력O가 있습니다. 먼저 출력 $O_1$은 convolution연산에 의해 아래 그림에 나온 식과 같이 나타낼 수 있습니다.
  
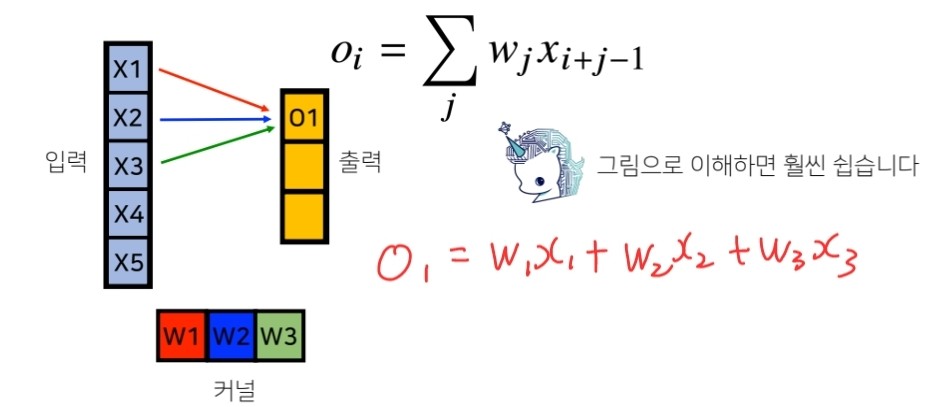
  이제 역전파를 해볼텐데, $\delta$는 미분값을 의미하고 L은 loss function을 의미합니다.
  
  
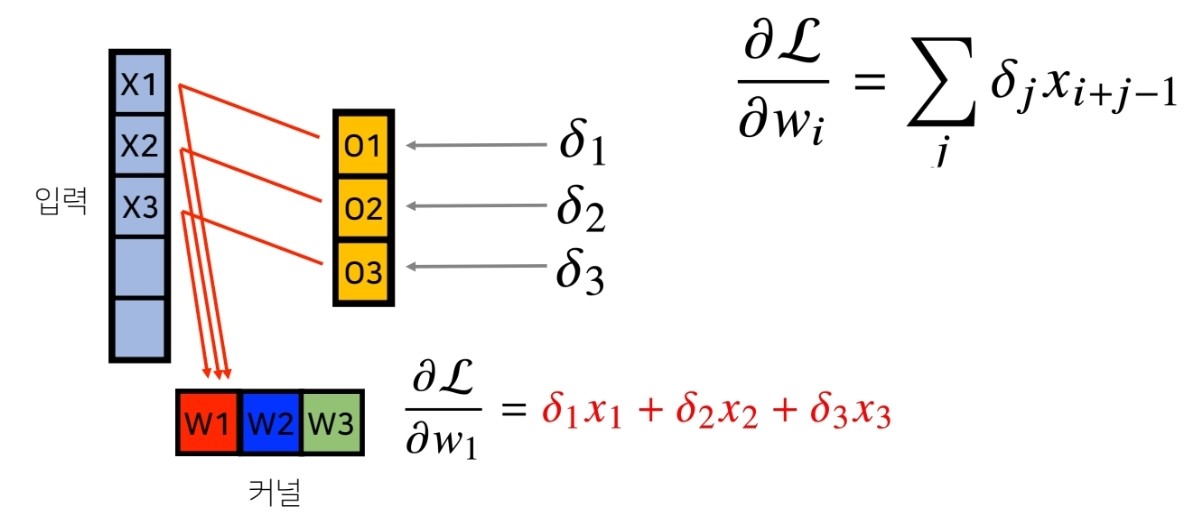
  역전파를 계산하여 보니, 미분값인 $\delta$에 입력벡터 x를 convolution 계산한 값이 나온 것을 확인할 수 있었습니다.
  
  

저는 이전에 CNN을 공부한 적이 있어서 이번 내용은 이해하기가 쉬웠습니다.
제가 느낀바로는 이번 CNN 첫걸음 강좌는 CNN에 대한 정말 기초적인 내용만 다뤄주신것 같고 나중에 더욱 심화된 내용을 다뤄주실 것 같습니다.