📌Historical Review

• 딥러닝의 주요 구성 요소
  • Data : 모델을 학습시키는 데이터
  • Model : 데이터를 뒤져 패턴을 발견하거나 예측을 수행하는 알고리즘의 표현식.
    같은 데이터와 Task가 주어졌다 하더라도, 모델의 성질에 따라 결과는 다르다.
  • Loss function : 데이터를 토대로 산출한 모델의 예측 값과 실제 값과의 차이를 표현하는 지표.
  • Algorithm : loss를 최소화하기 위해 매개변수를 조정

📌Neural Networks & MLP

Neural Networks

• 인공신경망(artificial neural network)은 기계학습과 인지과학에서 생물학의 신경망에서 영감을 얻은 통계학적 학습 알고리즘이다.(위키백과)
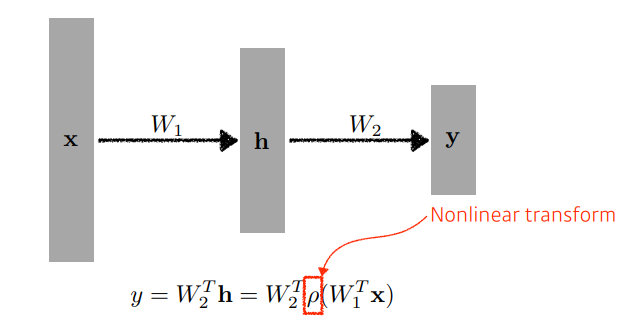
• 즉, 신경망은 비선형 변환이 뒤따르는 affine transformation을 모아놓은 함수라고 할 수 있다.

Linear Neural Networks

아래 그림과 같이 가장 간단한 선형모델의 예를 보자.

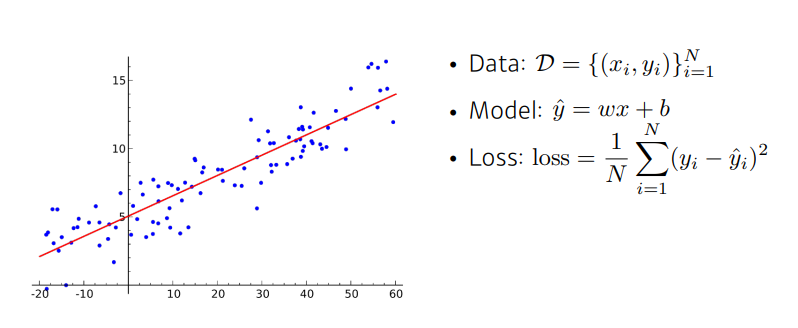
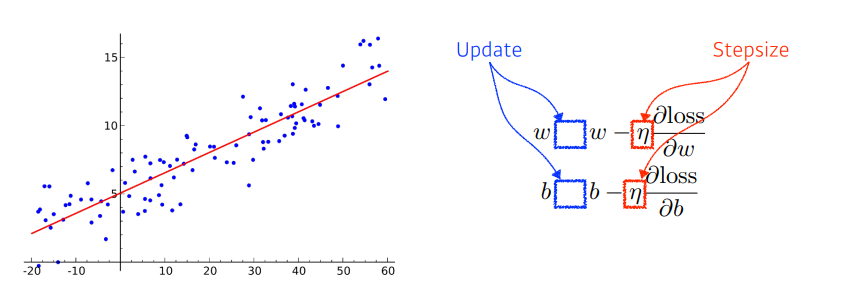
우리는 모델의 예측 값과 실제 값의 차이를 표현하는 지표인 Loss를 정하고, 그 Loss를 최소화하는 것을 목표한다. 이를 위해서는 최적화 변수에 대한 편미분을 다음과 같이 계산할 수 있다.

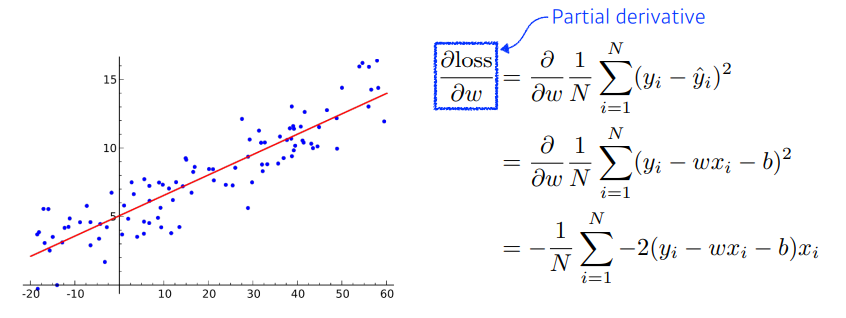
이후 우리는 loss가 줄어드는 방향으로 가중치를 다음과 같이 업데이트 할 수 있고, 이와 같은 방법을 Gradient Descent 라 부른다.

다차원 입출력을 다루기 위해서는 다음과 같이 행렬을 사용한다.

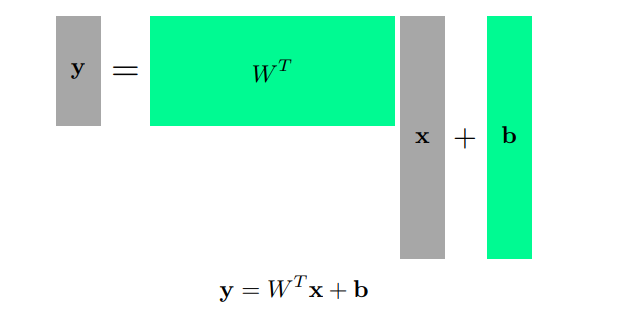
이때 가중치 행렬 W를 해석하는 한 가지 방법은, 벡터간 공간의 변환을 해준다고 생각을 하면 된다. 즉, 입력 벡터 x를 공간 변환 시켜 특징을 더욱 잘 알아낼 수 있게 공간 변환을 시킨 벡터 y를 만들어 준다 생각하면 되겠다. affine transformation 이라고 한다.

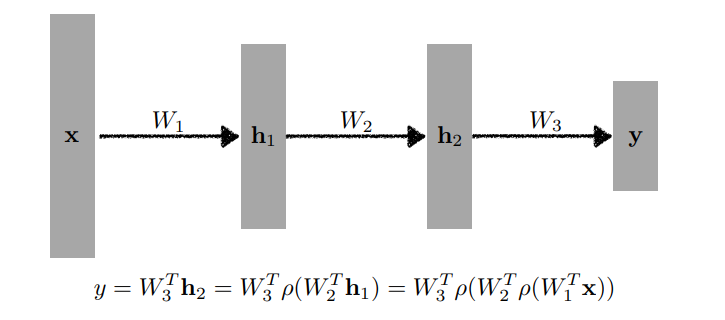
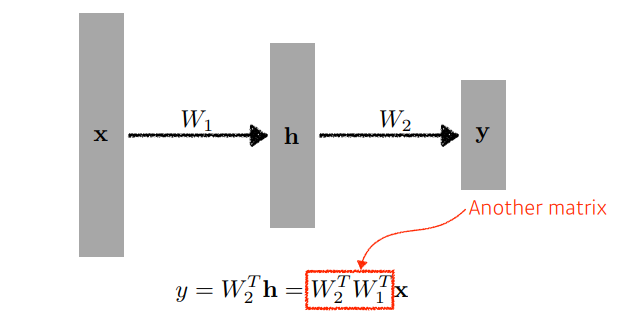
물론 이러한 layer을 여러 개 쌓을 수 있다.

하지만 이런 선형분류기의 한계가 나타난 계기가 있다. 바로 XOR문제 이다.

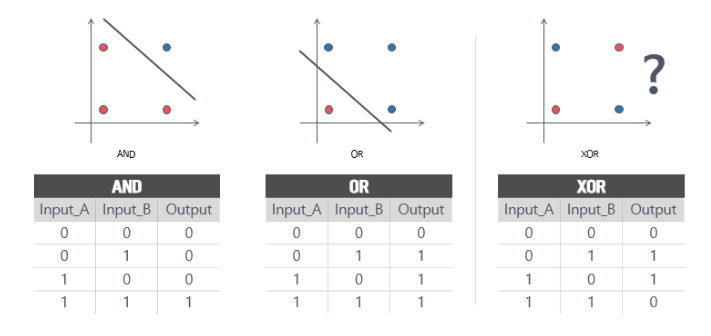
위 그림에서 확인할 수 있듯이 기존 퍼셉트론은 AND 문제와 OR 문제는 해결할 수 있지만, XOR과 같은 non-linear 문제는 해결할 수 없었다.
이를 해결하기 위해 나온 개념이 hidden layer이다. 하지만 선형 분류기로는 이 hidden layer을 만드는데 어려움이 있는데, 선형 시스템이 아무리 깊어지더라도 f(ax+by) = af(x) + bf(y) 의 성질 때문에 아무리 많이 layer을 쌓아도 하나의 linear 연산으로 나타낼 수 있기 때문이다.

이에 대한 해결방안이 바로 활성화 함수(activation function) 이다.
활성화 함수를 사용하면 입력값에 대한 출력값이 linear하게 나오지 않으므로 선형분류기를 비선형 시스템으로 만들 수 있다.
따라서 MLP(Multiple layer perceptron) 는 단지 linear layer를 여러개 쌓는 개념이 아닌 활성화 함수를 이용한 non-linear 시스템을 아래 그림과 같이 여러 layer로 쌓는 개념이다.