Vector

• n-dimensional coordinate system
  n개의 값으로 표현하는 n차원의 좌표계
  

vector

* vector = length+direction

• Dot Product( Scalar Product, inner Product )
  
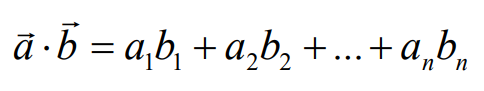
  = 결과값이 scala

• Cross Product( Vector Product )
  A=[a1,a2,a3],B=[b1,b2,b3]
  AXB = (a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)

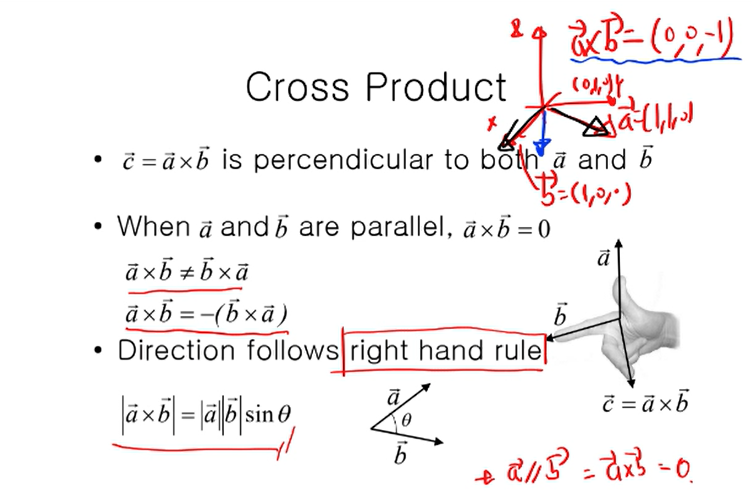
Linear independent

linearly independent는 선형적으로 독립한다는 의미로 선형 독립하는 벡터의 수에 따라 벡터 공간을 결정짓는 중요한 요소가 된다.

선형 독립을 평가하는 방식은 아래와 같다.

두 개의 벡터 v1 = (1,1), v2 = (-3,2) 가 있고 이를 선형 결합해서 0이되는 식을 만들어 보자.

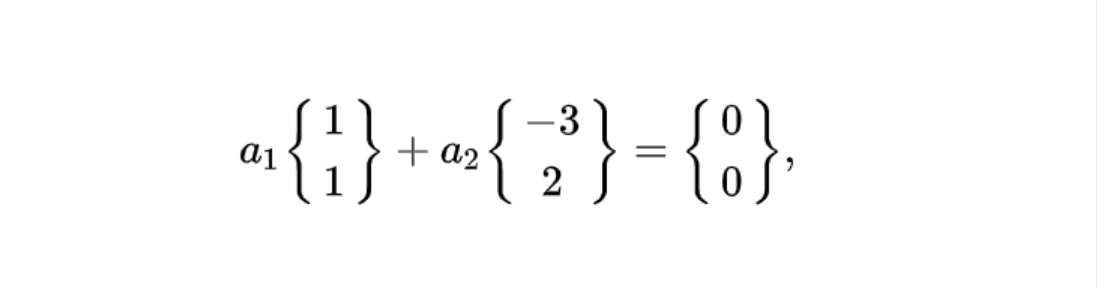
이를 행렬로 표현 하면

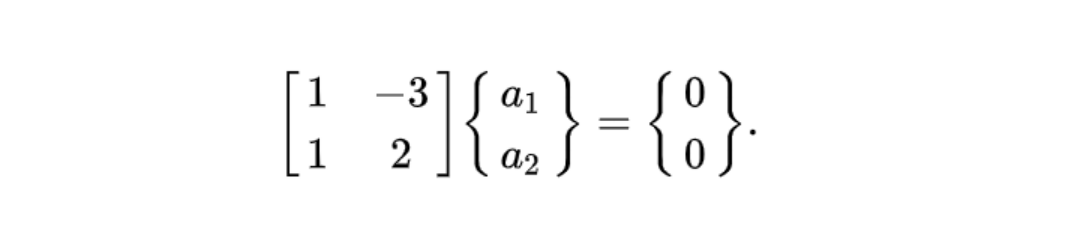
다시 표현한 행렬을 행 연산하면

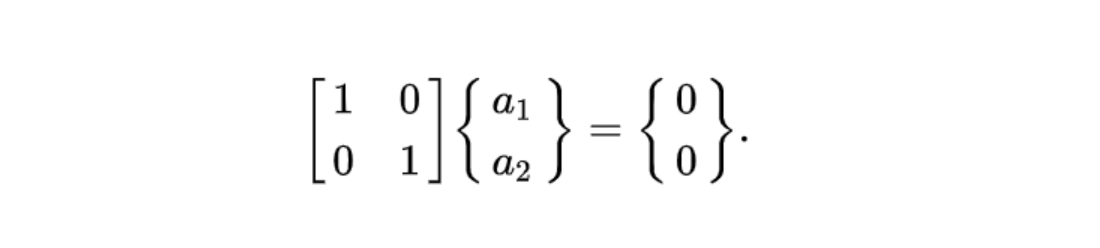
위와 같은 방정식을 만족하기 위해서는 a1과 a2는 0 이외에는 존재하지 않을 때 이를 linearly independent하다 라고 할 수 있다.

반대로 위와 같은 선형 결합, 행렬 연산을 통해 non-zero solution이 존재한다면 그 벡터들은 linearly dependent하다고 할 수 있으며 linearly dependent 관계에 존재하는 벡터들은 한 벡터를 다른 벡터들로 표현 가능하다.

Line segment

line 내에서 parametin variable을 이용해 two end point를 잡아 line의 일부분을 벡터화 시켜 표현 가능하다.

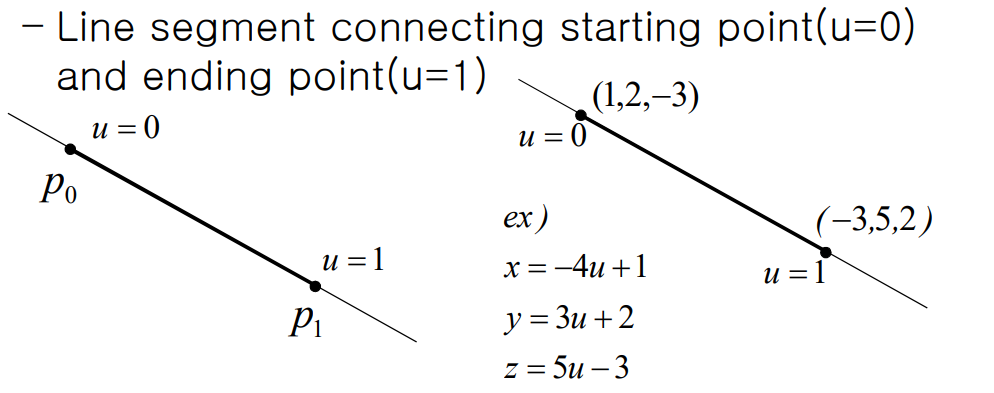
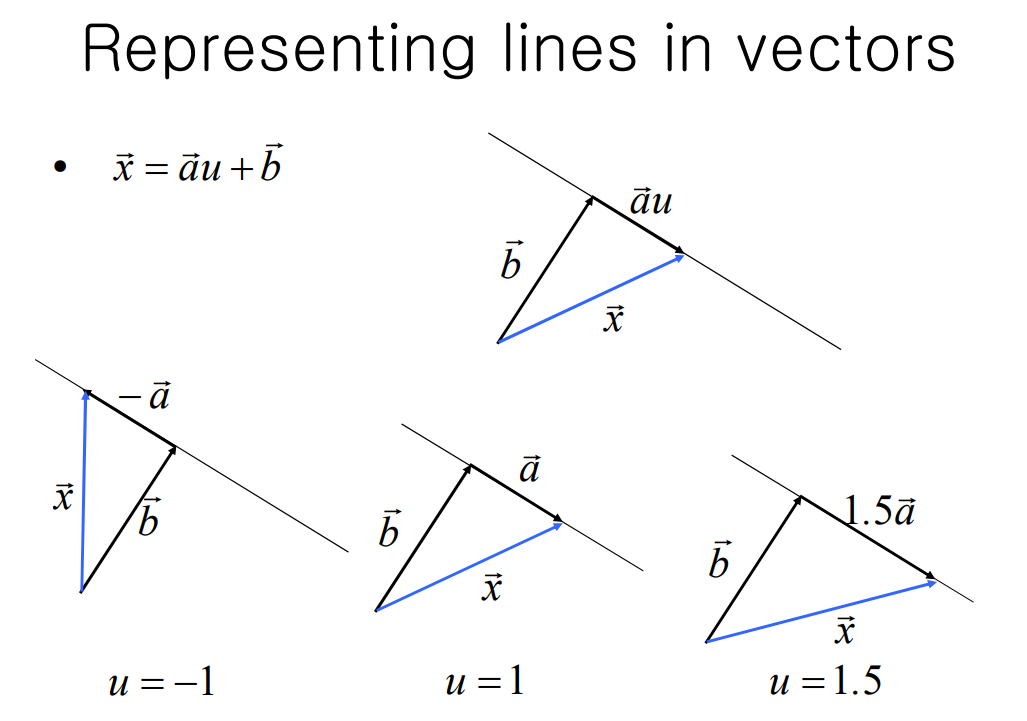
Lines and Planes

어떤 line의 벡터 a와 평면의 노멀벡터 n이 있다 했을 때, a(dot)n == 0 이라면 line과 평면은 평행하다. 그렇지 않다면 한 포인트에서 intersect한다.