Matrix

Matrix Computation

Matrix 특성 : AI = IA = A

Determinant

행렬식. 정방행렬에서 정의되는 것으로 어떤 계산식에 따라 행렬의 원소들을 대입하여 얻은 수치로 행렬의 특성을 결정짓는 값을 의미한다.

A라는 행렬이 존재할 때 A의 Determinant는 |A| 또는 det(A)라고 표현한다.

행렬식의 기하학적인 관점에서 잠깐 살펴보면 "행렬식은 선형변환 후의 기저벡터들이 이루고 있는 공간의 넓이"로 해석도 가능하다.

Computation

Determinant의 특성 : |A|=|A^T|, |AB|=|A||B| , row에 상수k를 곱할경우 determinat의 값도 k만큼 커진다.

Inner Product & Outer Product

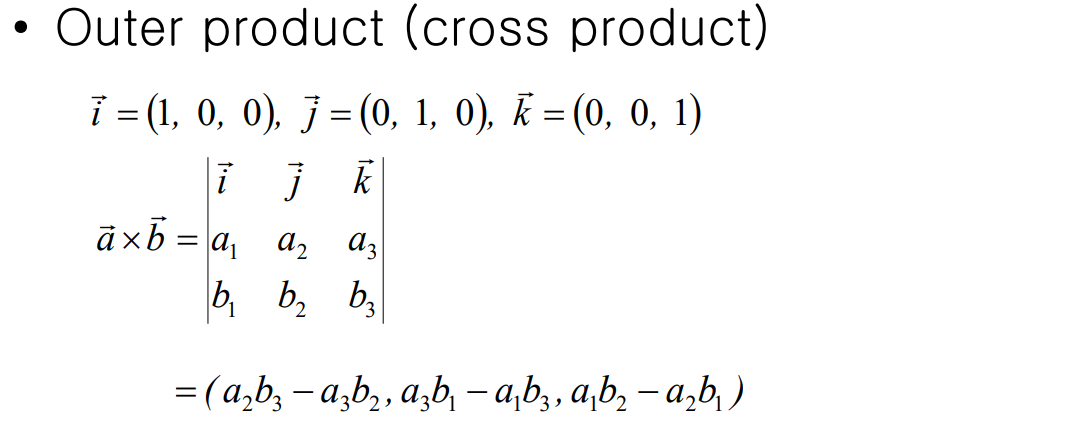
Inverse Matrix

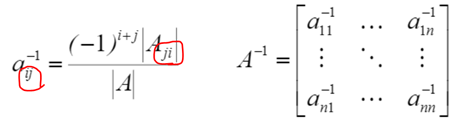
Invese Matrix의 특징 : det(A)=0이라면 A의 Inverse Matrix는 존재하지 않는다.

Linear System

Eigenvalues and Eigenvectors

정의 : 정방행렬 A에 대한 어떤 벡터 v(x,y)에서 V(X,Y)로의 변환에서, 어떤 λ가 상수일 때, V= λv을 만족하는 벡터 v을 고유벡터(Eigenvector), λ를 고유값(Eigenvalue)라고 한다.

Diagonalization

대각화 의미 참고 : https://blog.naver.com/spin898/221148112590

추가 연산.