동형암호
Craig Gentry가 2009년에 제안한 fully homomorphic scheme
인수분해 문제 (Factoring Problem)
N=pq(N:2048 bit, p, q: 1024 bit)- N이 주어졌을 때 소수 p, q를 찾는건 어렵지만 p,q를 곱해서 N을 얻는 건 쉬움
- N, p, q가 Polynomial일 경우도 같은 문제!
정의
z = F(x, y)
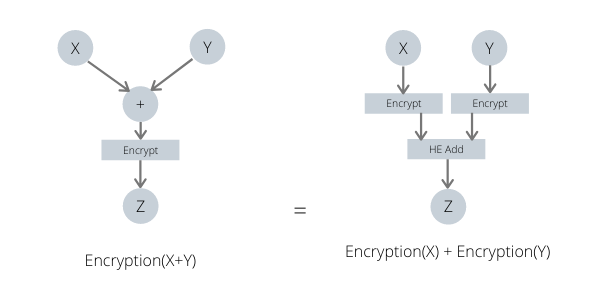
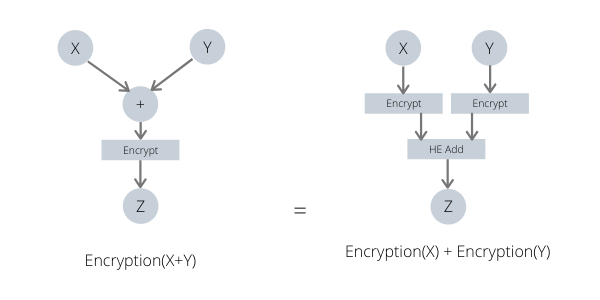
he_encrypt(F(x, y)) = F(he_encrypt(x), he_encrypt(y))- HE scheme을 이용해 함수 F를 암호화된 데이터로 연산
- 함수 F는 일반적으로 덧셈이나 곱셈
- HE를 이용해 클라우드에 암호화된 데이터를 업로드
- 클라우드에서는 암호화된 데이터로 연산을 수행하고 나중에 클라이언트가 연산 결과를 복호화
- 이 일련의 과정은 클라이언트가 서버와 online이 아니어도 상관없기 때문에 MPC에 비해 큰 이점.
특징
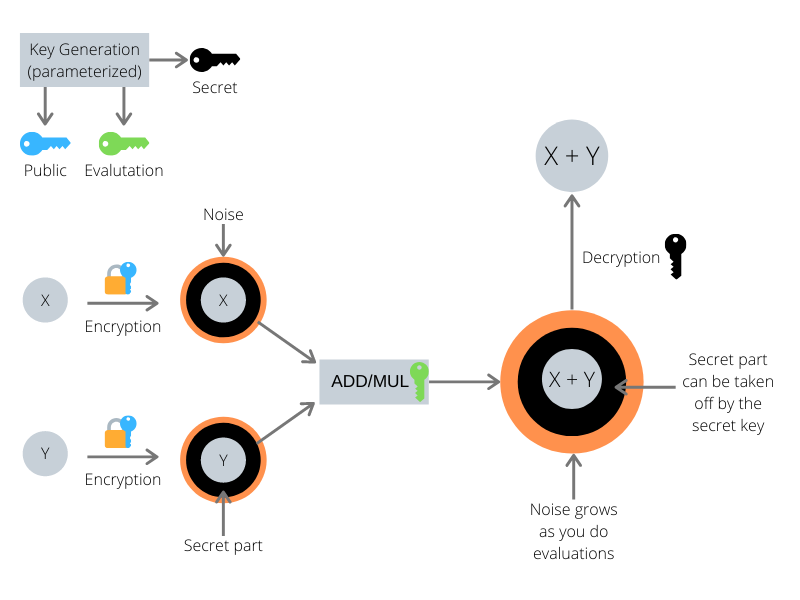
- lattice, RLWE 기반의 HE scheme을 사용할 경우 ciphertext로 암호화할 때 plaintext에 secret key와 노이즈를 이용해 제거할 수 있는 secret part를 더해주는 방식을 사용함
Enc(m; sk) -> (a*s + m + 2e, -a) - ciphertext로 연산을 진행할 경우 노이즈가 곱해지고 더해지면서 노이즈가 증가하게됨
- plaintext를 복호화 할 수 없을 정도로 노이즈가 증가하지 않도록 parameter를 잘 조절해야함
HE의 종류
-
Partial-HE (PHE) : 곱셈, 덧셈 중 하나만 되는 것. Elgamal('x'), Paillier('+')
-
Somewhat-HE (SHE) : 곱셈, 덧셈 전부 가능하나 제한된 횟수 만큼 가능. Exponential하게 parameter 필요
-
Leveled-HE (LHE) : 곱셈, 덧셈 전부 가능하나 제한된 횟수 만큼 가능. Linear하게 parameter 필요
-
Fully-HE (FHE) : 제한 없이 곱셈, 덧셈 모두 가능
