동형암호 - 2. (R)LWE

WonderIT·2022년 3월 15일
LWERLWE동형암호

Homomorphic Encryption

목록 보기
2/2

(Ring) Learning With Errors

  • Introduced by Lyubashevsky, Peikert and Regev (Eurocrypt 2010)

Factoring problem

e.g.:

3s1+5s2+8s3+e1=279s1+7s2+s3+e2=31s1+2s2+s3+e3=73s_1 + 5s_2+8s_3 + e_1 = 27 \\ 9s_1 + 7s_2+s_3 + e_2 = 31 \\ s_1 + 2s_2+s_3 + e_3 = 7 \\
  • 노이즈(eme_m)가 없을 경우 : s1∼sns_1 \sim s_n, m≥nm \geq n이면 연립 방정식의 해가 존재 (m은 방정식의 수)
  • 노이즈(eme_m)가 있을 경우 : m≥nm \geq n 이더라도 풀기 힘듬

RLWE

Basic Notation

  • Zq\mathbb{Z}_q: 정수의 집합 (−q/2,q/2](-q/2, q/2], (q는 q>1인 정수)
  • 모든 연산은 대부분 mod qmod \space q가 수행되고 양수인 정수 [0,q)[0,q)를 주로 다룰 수 있지만 이는 Zq\mathbb{Z}_q와 동일.
    −x≡q−x(mod q)-x\equiv q-x(mod \space q) (e.g.: −1≡6(mod 7))-1 \equiv 6(mod \space 7))
  • [⋅]m[⋅]_m : modulo m 적용
  • ⌊⋅⌉⌊⋅⌉ : 가까운 정수로 반올림
  • a,b∈Zqna, b \in \mathbb{Z}_q^n, a, b의 내적
    <a,b>=∑inai⋅bi(mod q)<a,b> = \sum_{i}^{n} a_i \cdot b_i (mod \space q)

Definition

Zq={0,1,2,⋯ ,q−1}Zqn=Zq×⋯×Zqa⃗∈Zqn=[a1,⋯ ,an] where ai∈ZqGiven a⃗∈Zqn,b⃗=a⃗⋅s⃗+e⃗,find s⃗∈Zqn\mathbb{Z}_q = \{0, 1, 2, \cdots, q-1\} \\ \mathbb{Z}_q^n = \mathbb{Z}_q \times \cdots \times \mathbb{Z}_q \\ \vec{a} \in \mathbb{Z}_q^n=[a_1, \cdots, a_n] \space where \space a_i \in \mathbb{Z}_q \\ Given \space \vec{a} \in \mathbb{Z}_q^n, \vec{b} = \vec{a} \cdot \vec{s} + \vec{e}, find \space \vec{s} \in \mathbb{Z}_q^n

e.g.:

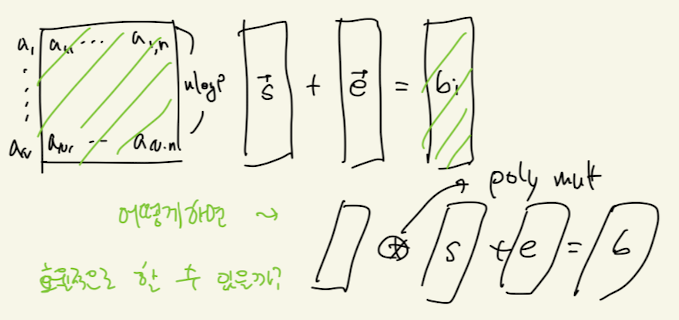
[357971121]⋅[s1s2s3]+[e1e2e3]=[27317]\begin{bmatrix} 3 & 5 & 7 \\ 9 & 7 & 1 \\ 1 & 2 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} s_1 \\ s_2 \\ s_3 \\ \end{bmatrix} + \begin{bmatrix} e_1 \\ e_2 \\ e_3 \\ \end{bmatrix} = \begin{bmatrix} 27 \\ 31 \\ 7 \\ \end{bmatrix} \\
[A]⋅[s]+[e]=[b]\begin{bmatrix} A \\ \end{bmatrix} \cdot \begin{bmatrix} s\\ \end{bmatrix} + \begin{bmatrix} e \\ \end{bmatrix} = \begin{bmatrix} b \\ \end{bmatrix}

LWE -> RLWE :

  • matrix multiplication 보다는 polynomial multiplication 이 더 빠름
  • A -> A'로 더 작은 공간에서 같은 식을 표현할 수 있음
[A′]∗[s]+[e]=[b]\begin{bmatrix} A^\prime \\ \end{bmatrix} * \begin{bmatrix} s\\ \end{bmatrix} + \begin{bmatrix} e \\ \end{bmatrix} = \begin{bmatrix} b \\ \end{bmatrix}

ring 에서 quotient prime을 이용해 modulo 연산을 하듯이 polynomial에서도 polynomial로 나눠주게됨.

Z→Zq:primeZ(x)→Z(x)/p(x)\mathbb{Z} \rarr \mathbb{Z}_q:prime \\ \mathbb{Z}(x) \rarr \mathbb{Z}(x)/p(x)

p(x)p(x): irreducable polynomials

  • xn+1:if n=2kx^n+1 : if \space n=2^k
  • xn+1x^n+1로 나눴다는 의미는 xn+1=0x^n+1=0으로 본다는 뜻
  • ∴ xn=−1\therefore \space x^n=-1
(a0+a1x)(s0+s1x)=a0s0+(a0s1+a1s0)x+a1s1x2 (if x2+1=0)=(a0s0−a1s1)+(a0s1+a1s0)x=b0+b1 x\begin{aligned} (a_0+a_1x)(s_0+s_1x) &= a_0s_0 &+ (a_0s_1+a_1s_0)&x + a_1s_1x^2 \space (if \space x^2+1=0) \\ &= (a_0s_0-a_1s_1) &+ (a_0s_1+a_1s_0)&x \\ &= b_0 &+ b_1 \space &x \\ \end{aligned}

Reference

profile
WonderIT
이전 포스트

동형암호 - 1. Introduction

0개의 댓글