3.1 MNIST
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', as_frame=False)mnist 로드
X, y = mnist.data, mnist.target- 70,000개의 이미지. 784개의 특성.
- 28 x 28 픽셀의 이미지
- 각 특성은 0~255까지의 픽셀 강도를 나타냄
import matplotlib.pyplot as plt
def plot_digit(image_data):
image = image_data.reshape(28, 28)
plt.imshow(image, cmap="binary")
plt.axis("off")
some_digit = X[0]
plot_digit(some_digit)
plt.show()
- cmap="binary"로 지정하여 0을 흰색, 255를 검은색으로 나타내는 흑백 컬러 맵 사용
- 숫자 5로 보이는 이 그림의 레이블은 5
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]- 훈련 세트(앞쪽 60,000개), 테스트 세트(뒤쪽 10,000개)
- 훈련 세트는 이미 섞여 있음 → 모든 교차 검증 폴드를 비슷하게 만들어 줌
3.2 이진 분류기 훈련
이진 분류기(binary classifier) : target일 경우만 true, 나머지는 모두 false
y_train_5 = (y_train == '5')
y_test_5 = (y_test == '5')from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([some_digit])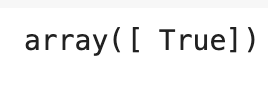
- 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 분류기로 처리
- SGD는 한 번에 하나씩 훈련 샘플을 독립적으로 처리할 수 있어서 온라인 학습에 적합
- 분류기는 해당 이미지가 5를 나타낸다고 추측(True)
3.3 성능 측정
3.3.1 교차 검증을 사용한 정확도 측정
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")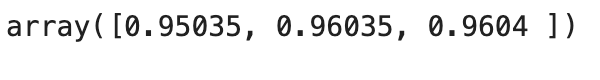
- 정확도(accuracy)가 모든 교차 검증 폴드에 대해 95% 이상
from sklearn.dummy import DummyClassifier
dummy_clf = DummyClassifier()
dummy_clf.fit(X_train, y_train_5)
print(any(dummy_clf.predict(X_train)))- False가 출력됨. True로 예측된 것이 없음.
cross_val_score(dummy_clf, X_train, y_train_5, cv=3, scoring="accuracy")- 정확도가 90% 이상
- 이미지의 10% 정도가 5이기 때문에 무조건 5가 아니라고 예측해도 정확히 맞출 확률이 90%
3.3.2 오차 행렬
불균형한 테이터셋을 다룰 때, 분류기의 성능을 평가하는 더 좋은 방법은 오차 행렬(confusion matrix)를 조사하는 것
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_train_5, y_train_pred)
cm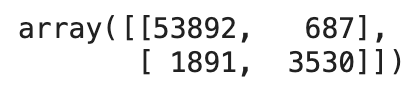
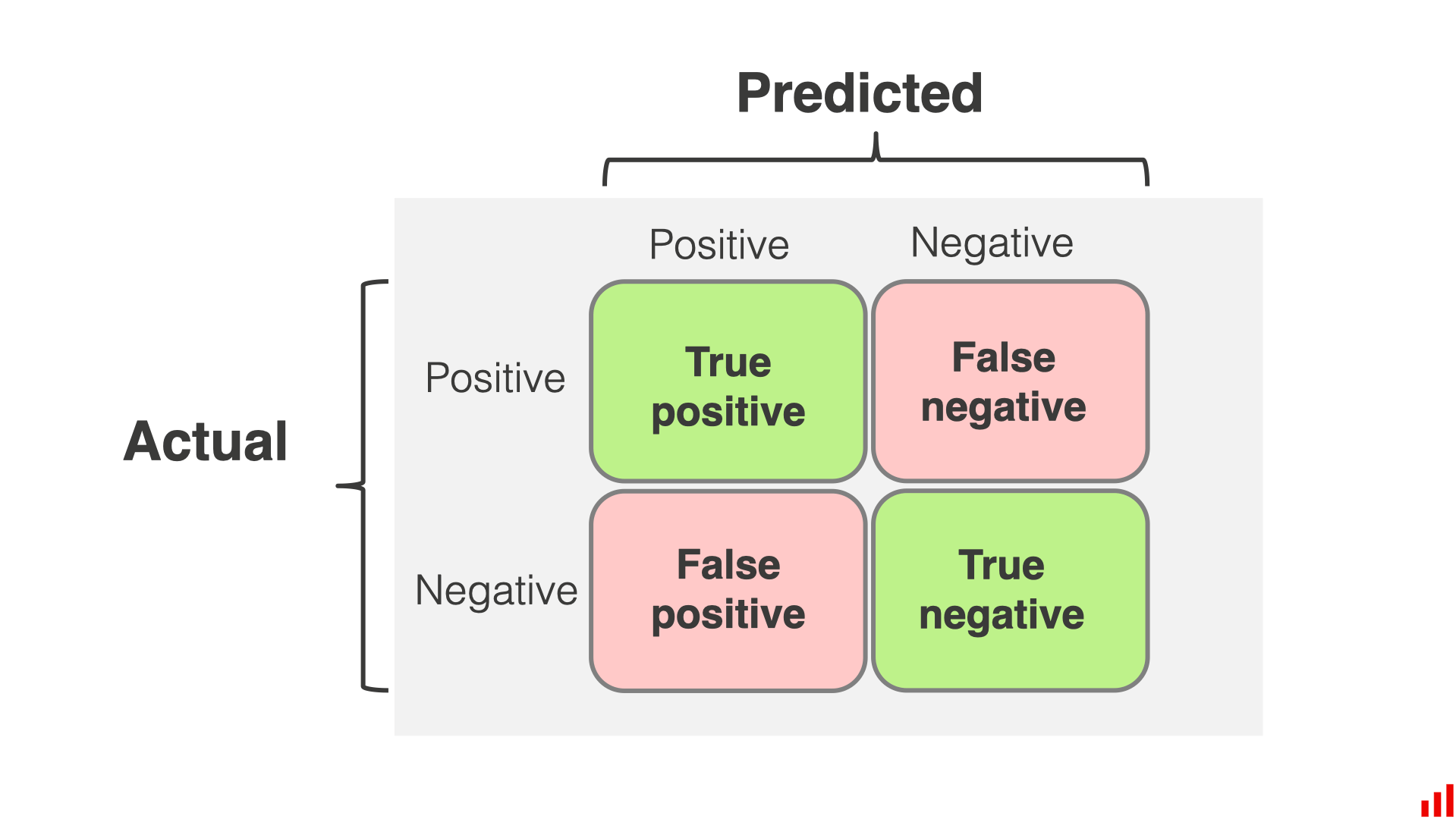
- 오차 행렬의 행은 실제 클래스, 열은 예측한 클래스
- 음성 클래스 (negative class) : '아닌 것'을 판별하는 클래스
- 진짜 음성 (true negative) : '아닌 것'을 '아닌 것'으로 잘 판별한 것
- 거짓 양성 (false negative) : '아닌 것'을 '맞는 것'으로 잘못 판별한 것
- 양성 클래스 (positive class) : '맞는 것'을 판별하는 클래스
- 거짓 음성 (false negative) : '맞는 것'을 '아닌 것'으로 잘못 판별한 것
- 진짜 양성 (true positive) : '맞는 것'을 '맞는 것'으로 잘 판별한 것
3.3.3 정밀도와 재현율
정밀도(precision)
- TP : 진짜 양성의 수
- FP : 거짓 양성의 수
재현율(recall)
- FN : 거짓 음성의 수
- 정밀도와 재현율을 같이 사용하는 것이 일반적임
- 민감도(sensitivity) 또는 진짜 양성 비율(true positive rate, TPR)이라고도 함
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred) # == 3530 / (687 + 3530)
recall_score(y_train_5, y_train_pred) # == 3530 / (1891 + 3530)F1 score
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)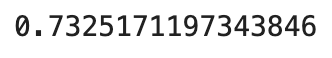
- F1 score는 정밀도와 재현율의 조화 평균(harmonic mean)
- F1 score가 높아지려면 재현율과 정밀도가 모두 높아야 함
- 상황에 따라 정밀도가 중요할 수도 있고 재현율이 중요할 수도 있음
3.3.4 정밀도/재현율 트레이드오프
정밀도/재현율 트레이드 오프 : 정밀도를 올리면 재현율이 줄고 그 반대도 마찬가지
SGDClassifier
- 결정 함수(decision function)을 사용하여 각 샘플의 점수를 계산
- 점수가 결정 임곗값(decision threshold)보다 크면 양성 클래스, 그렇지 않으면 음성 클래스
적절한 임곗값 정하기
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)- cross_val_predict() 함수를 이용해 훈련 세트에 있는 모든 샘플의 점수를 구함
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)- 이전 코드에서 구한 점수를 바탕으로 precision_recall_curve() 함수를 사용하여 가능한 모든 임곗값에 대해 정밀도와 재현율 계산
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g--", label="Recall", linewidth=2)
plt.vlines(threshold, 0, 1.0, "k", "dotted", label="Threshold")
idx = (thresholds >= threshold).argmax()
plt.plot(thresholds[idx], precisions[idx], "bo")
plt.plot(thresholds[idx], recalls[idx], "go")
plt.axis([-50000, 50000, 0, 1])
plt.grid()
plt.xlabel("Threshold")
plt.legend(loc="center right")
plt.show()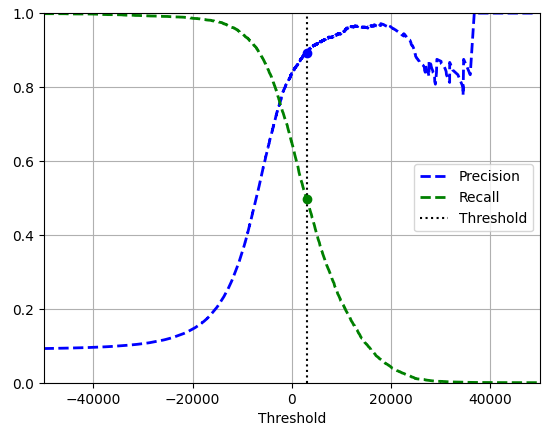
- 해당하는 임곗값(3,000)에서 정밀도는 약 90%, 재현율은 약 50%
import matplotlib.patches as patches # 구부러진 화살표를 그리기 위해서
plt.figure(figsize=(6, 5))
plt.plot(recalls, precisions, linewidth=2, label="Precision/Recall curve")
plt.plot([recalls[idx], recalls[idx]], [0., precisions[idx]], "k:")
plt.plot([0.0, recalls[idx]], [precisions[idx], precisions[idx]], "k:")
plt.plot([recalls[idx]], [precisions[idx]], "ko",
label="Point at threshold 3,000")
plt.gca().add_patch(patches.FancyArrowPatch(
(0.79, 0.60), (0.61, 0.78),
connectionstyle="arc3,rad=.2",
arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
color="#444444"))
plt.text(0.56, 0.62, "Higher\nthreshold", color="#333333")
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")
plt.show()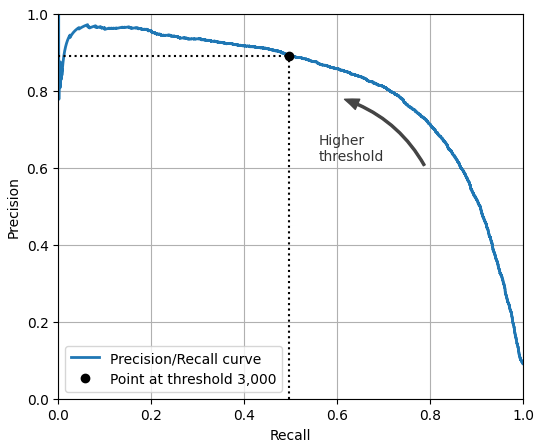
- 재현율 80% 근처에서 정밀도가 급격하게 줄어드는 양상. 이 하강점 직전을 정밀도/재현율 트레이드오프로 선택하는 것이 좋음.
idx_for_90_precision = (precisions >= 0.90).argmax()
threshold_for_90_precision = thresholds[idx_for_90_precision]
threshold_for_90_precision
# 3370.0194991439557- 정밀도가 최소 90%가 되는 가장 낮은 임곗값
y_train_pred_90 = (y_scores >= threshold_for_90_precision)
precision_score(y_train_5, y_train_pred_90)
# 0.9000345901072293
recall_at_90_precision = recall_score(y_train_5, y_train_pred_90)
recall_at_90_precision
# 0.4799852425751706- 정밀도 90%를 달성한 분류기를 만들었지만, 재현율 48%는 부족한 값임
3.3.5 ROC 곡선
- FPR(false positive rate)에 대한 TPR(true positive rate)의 곡선
- FPR은 1에서 TNR(true negative rate)을 뺀 값
- TNR을 특이도(specificity)라고도 함
- ROC 곡선은 민감도에 대한 1-특이도 그래프
from sklearn.metrics import roc_curve
fpr, tpr, tresholds = roc_curve(y_train_5, y_scores)
idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]
plt.plot(fpr, tpr, linewidth=2, label="ROC curve")
plt.plot([0, 1], [0, 1], 'k:', label="Random classifier's ROC curve")
plt.plot([fpr_90], [tpr_90], "ko", label="Threshold for 90% precision")
plt.gca().add_patch(patches.FancyArrowPatch(
(0.20, 0.89), (0.07, 0.70),
connectionstyle="arc3,rad=.4",
arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
color="#444444"))
plt.text(0.12, 0.71, "Higher\nthreshold", color="#333333")
plt.xlabel('False Positive Rate (Fall-Out)')
plt.ylabel('True Positive Rate (Recall)')
plt.grid()
plt.axis([0, 1, 0, 1])
plt.legend(loc="lower right", fontsize=13)
plt.show()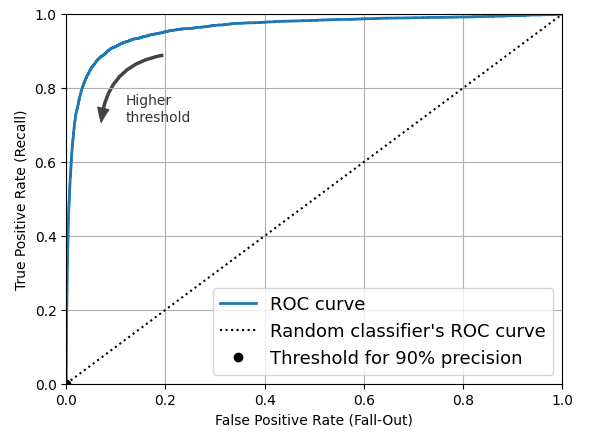
- TPR이 높을수록 FPR이 증가
- 좋은 분류기는 점선에서 멀리 떨어져야 함(왼쪽 위로)
- AUC(area under the curve) 측정을 통해 분류기들을 비교할 수 있음
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
y_scores_forest = y_probas_forest[:, 1]
precisions_forest, recalls_forest, thresholds_forest = precision_recall_curve(
y_train_5, y_scores_forest
)
plt.plot(recalls_forest, precisions_forest, "b-", linewidth=2,
label="Random Forest")
plt.plot(recalls, precisions, "--", linewidth=2, label="SGD")
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")
plt.show()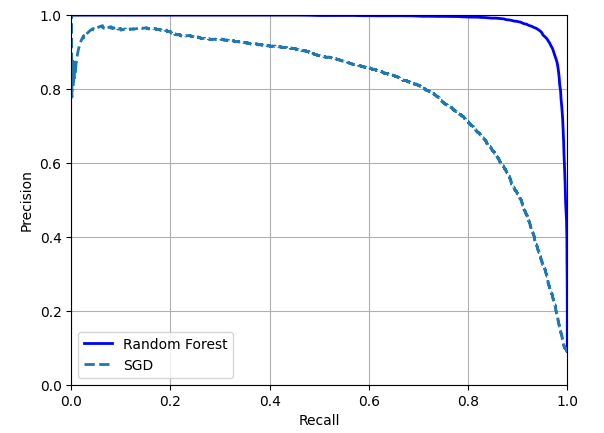
- RandomForestClassifier의 PR곡선이 SGDClassifier의 곡선보다 훨씬 더 좋아보임
- F1 Score과 ROC AUC 점수도 모두 우수
from sklearn.metrics import roc_auc_score
y_train_pred_forest = y_probas_forest[:, 1] >= 0.5
f1_score(y_train_5, y_train_pred_forest)
# 0.9274509803921569
roc_auc_score(y_train_5, y_scores_forest)
# 0.99834367313281453.4 다중 분류
다중 분류기(multiclass classifier)는 둘 이상의 클래스를 구별할 수 있음
이진 분류기를 여러 개 사용해 다중 클래스를 분류하는 기법
- OvR(one-versus-the-rest)
- 목표하는 특정 타깃과 나머지를 분류.
- 클래스 N개를 구분하기 위해 분류기 N개를 훈련
- OvA(one-versus-all) 이라고도 함
- ex) 1 ~ 10까지의 숫자 중에서 1만 분류
- OvO(one-versus-one)
- 각 조합마다 이진 분류기를 훈련
- 클래스 N개를 구분하기 위해 분류기 N × (N - 1) / 2개를 훈련
- ex) 1 ~ 10까지의 숫자 분류를 위해 0과 1구별, 0과 2 구별, 1과 2 구별 등과 같이 각 숫자의 조합마다 분류기를 훈련
- OvO의 장점은 전체 훈련 세트 중 구별할 두 클래스에 해당하는 샘플만 있으면 된다는 점
- 일부 알고리즘은 OvO를 선호하지만, 대부분의 이진 분류 알고리즘에서는 OvR을 선호함
- 다중 클래스 분류 작업에 이진 분류 알고리즘을 선택하면 사이킷런이 자동으로 OvR 또는 OvO를 실행함
from sklearn.svm import SVC
svm_clf = SVC(random_state=42)
svm_clf.fit(X_train[:2000], y_train[:2000])
svm_clf.predict([some_digit])
# array(['5'], dtype=object)
some_digit_scores = svm_clf.decision_function([some_digit])
some_digit_scores.round(2)
# array([[ 3.79, 0.73, 6.06, 8.3 , -0.29, 9.3 , 1.75, 2.77, 7.21, 4.82]])
# 가장 높은 점수는 9.3이고 클래스 5에 해당함
class_id = some_digit_scores.argmax()
class_id
# 5
svm_clf.classes_
# array(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], dtype=object)
svm_clf.classes_[class_id]
# '5'from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(random_state=42))
ovr_clf.fit(X_train[:2000], y_train[:2000])
ovr_clf.predict([some_digit])
# array(['5'], dtype='<U1')
len(ovr_clf.estimators_)
# 10
# 10개의 분류기가 훈련되었음
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
# array(['3'], dtype='<U1')
sgd_clf.decision_function([some_digit]).round()
# array([[-31893., -34420., -9531., 1824., -22320., -1386., -26189., -16148., -4604., -12051.]])
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
# array([0.87365, 0.85835, 0.8689])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_trian_scaled = scaler.fit_transform(X_train.astype("float64"))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
# array([0.8983, 0.891, 0.9018])- SVC 기반으로 OvR 전략을 강제하여 만든 다중 분류기
- SGDClassifier를 훈련하고 예측을 만들었음
- some_digit에 대해서는 '3'으로 예측을 잘못함 (정답은 '5')
- 전체 테스트 폴드에 대해서는 85.8% 이상의 성능을 보임
- 입력의 scale을 조정하여 정확도를 89% 이상으로 높임
3.5 오류 분석
from sklearn.metrics import ConfusionMatrixDisplay
y_train_pred = cross_val_predict(sgd_clf, X_train,scaled, y_train, cv=3)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred)
plt.show()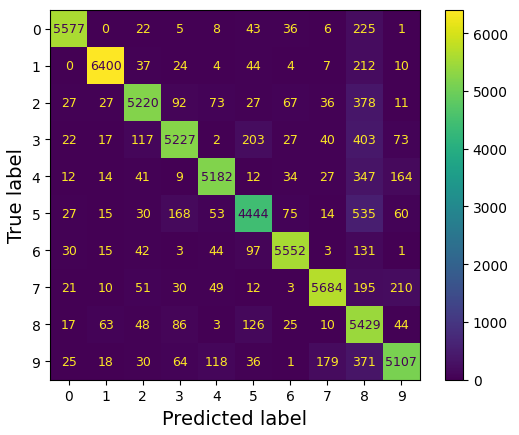
- 대부분의 이미지가 주대각선에 위치함 = 이미지가 올바르게 분류됨
- 모델이 5에서 더 많은 오류를 범했거나 데이터 집합에 다른 숫자보다 5가 적기 떄문에 5번 행과 5번 열의 대각선에 있는 셀은 다른 숫자보다 약간 더 어둡게 보임 → 정규화로 해결
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
normalize="true", values_format=".0%")
plt.show()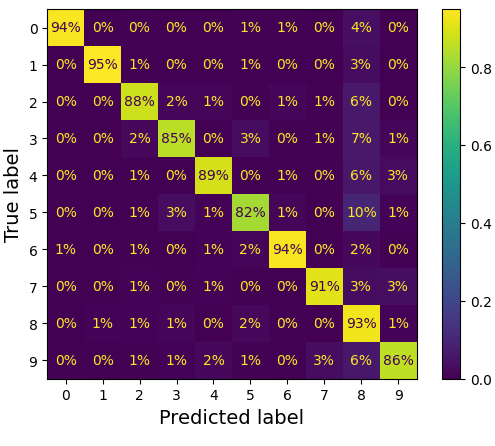
- 각 값을 해당 클래스의 총 이미지 수로 나누어 오차 행렬을 정규화 (normalize="true")
- '5' 중에서 82%가 올바르게 분류됨
- 가장 많은 오류는 '8'으로 잘못 분류한 것 (10%)
sample_weight = (y_train_pred != y_train)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
sample_weight=sample_weight,
normalize="true", values_format=".0%")
plt.show()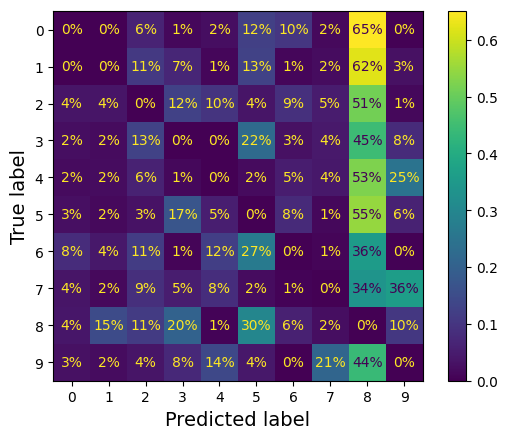
- 올바른 예측에 대한 가중치를 0으로 하여 오류가 더 눈에 띄도록 함
- 많은 이미지가 '8'으로 잘못 분류되었음을 알 수 있음
- 이 그래프에서는 올바른 예측이 제외되어 있음. 1행 9열의 경우 '0'이미지에서 발생한 오류 중 65%가 '8'으로 잘못 분류되었다는 의미임
sample_weight = (y_train_pred != y_train)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
sample_weight=sample_weight,
normalize="pred", values_format=".0%")
plt.show()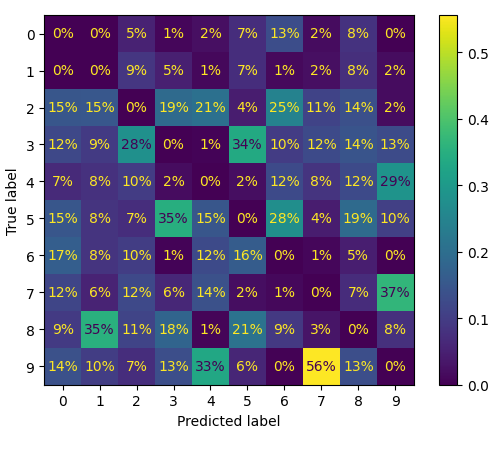
- 오차 행렬을 열 단위로 정규화
오차 행렬을 분석하면 분류기의 성능 향상 방안에 관한 인사이트를 얻을 수 있음
cl_a, cl_b = '3', '5'
X_aa = X_train[(y_train ==cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train ==cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train ==cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train ==cl_b) & (y_train_pred == cl_b)]
size = 5
pad = 0.2
plt.figure(figsize=(size, size))
for images, (label_col, label_row) in [(X_ba, (0, 0)), (X_bb, (1, 0)),
(X_aa, (0, 1)), (X_ab, (1, 1))]:
for idx, image_data in enumerate(images[:size*size]):
x = idx % size + label_col * (size + pad)
y = idx // size + label_row * (size + pad)
plt.imshow(image_data.reshape(28, 28), cmap="binary",
extent=(x, x + 1, y, y + 1))
plt.xticks([size / 2, size + pad + size / 2], [str(cl_a), str(cl_b)])
plt.yticks([size / 2, size + pad + size / 2], [str(cl_b), str(cl_a)])
plt.plot([size + pad / 2, size + pad / 2], [0, 2 * size + pad], "k:")
plt.plot([0, 2 * size + pad], [size + pad / 2, size + pad / 2], "k:")
plt.axis([0, 2 * size + pad, 0, 2 * size + pad])
plt.xlabel("Predicted label")
plt.ylabel("True label")
plt.show()
- 3과 5는 매우 비슷한 모양을 가진 숫자라 오류가 많이 발생함
- 분류기는 이미지의 위치나 회전 방향에 매우 민감함
- 이미지를 중앙에 위치시키고 회전되어 있지 않도록 전처리하면 성능 향상을 기대할 수 있음
- 데이터 증식(data augmentation) : 훈련 이미지를 약간 이동시키거나 회전된 변형 이미지로 훈련 집합을 보강하는 방식
3.6 다중 레이블 분류
다중 레이블 분류 시스템(multilabel classification) : 여러 개의 이진 label을 출력하는 분류 시스템
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= '7')
y_train_odd = (y_train.astype('int8') % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
knn_clf.predict([some_digit])
# array([[False, True]])
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")
# 0.976410265560605- 이 코드는 모든 레이블의 가중치가 같다고 가정함
- multilabel의 첫 번째 값은 7보다 큰 값인지 나타내고 두 번째는 홀수인지 나타냄
- 숫자 5는 크지 않고(False), 홀수(True)임 → 알맞게 분류
레이블에 클래스의 지지도(타깃 레이블에 속한 샘플 수)를 가중치로 설정하면, 레이블에 속한 데이터의 수가 다른 경우에 생기는 문제를 방지할 수 있음.
from sklearn.multioutput import ClassifierChain
chain_clf = ClassifierChain(SVC(), cv=3, random_state=42)
chain_clf.fit(X_train[:2000], y_multilabel[:2000])
chain_clf.predict([some_digit])
# array([[0., 1.]])- ClassifierChain 클래스를 사용해 예측을 한 코드임
- SVC와 같이 기본적으로 다중 레이블 분류를 지원하지 않는 경우 레이블당 하나의 모델을 학습시킬 수 있음. 하지만 레이블 간의 의존성을 포착하기 어려움
- 큰 수(7, 8, 9)는 짝수일 확률보다 홀수일 확률이 2배 더 높지만 '홀수' 레이블에 대한 분류기는 '큰 값' 레이블 분류기가 무엇을 예측했는지 알 수 없음 → 모델을 체인으로 구성함으로써 해결 가능.
3.7 다중 출력 분류
다중 출력 다중 클래스 분류(multioutput-multiclass classification) : 다중 레이블 분류에서 한 레이블이 다중 클래스가 될 수 있도록 일반화한 것
- noise가 많은 숫자 이미지를 입력으로 받아 깨끗한 숫자 이미지를 배열로 출력
- 분류기의 출력이 다중 레이블(픽셀당 한 레이블)이고 각 레이블은 값을 여러 개 가짐(0~255) → 다중 출력 분류 시스템
np.random.seed(42)
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
plt.subplot(121); plot_digit(X_test_mod[0])
plt.subplot(122); plot_digit(y_test_mod[0])
plt.show()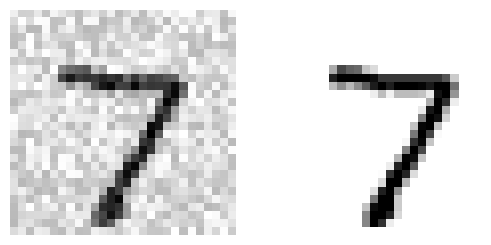
- randint() 함수를 사용하여 픽셀 강도에 noise 추가
- target 이미지는 원본 이미지
- 좌 : noise 추가한 이미지 / 우 : 원본 이미지
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[0]])
plot_digit(clean_digit)
plt.show()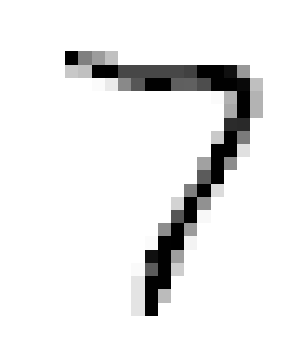
- target과 매우 비슷한 결과물을 출력
