[ML/Python] 분류(1) - 결정 트리, 앙상블 학습, 랜덤 포레스트

uwonj·2023년 10월 3일

머신러닝

01. 분류의 개요

지도학습: 레이블(Label), 즉 명시적인 정답이 있는 데이터가 주어진 상태에서 학습하는 머신러닝 방식
지도학습의 대표 유형인 '분류(Classification)'
- 학습 데이터로 주어진 데이터의 피처와 레이블값(결정 값, 클래스 값)을 머신러닝 알고리즘으로 학습해 모델 생성
  → 이렇게 생성된 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측
  → 기존 데이터가 어떤 레이블에 속하는지 패턴을 알고리즘으로 인지한 뒤 새로운 데이터가 어떤 레이블에 속하는지 판별하는 것
분류는 다양한 머신러닝 알고리즘으로 구현 가능하다.
e.g. 나이브 베이즈, 로지스틱 회귀, 결정 트리, 서포트 벡터 머신, 신경망, 앙상블 등
앙상블 (Ensemble): 서로 다른/같은 알고리즘을 단순히 결합한 형태도 존재, 일반적으로는 배깅(Bagging)과 부스팅(Boosting) 방식으로 나뉜다.
- 배깅: 랜덤 포레스트(Random Forest)가 대표적
- 부스팅: 그래디언트 부스팅(Gradient Boosting), XgBoost, LightGBM
- 앙상블의 기본 알고리즘으로는 일반적으로 '결정 트리'가 사용된다.

02. 결정 트리 (Decision Tree)

: 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만드는 것

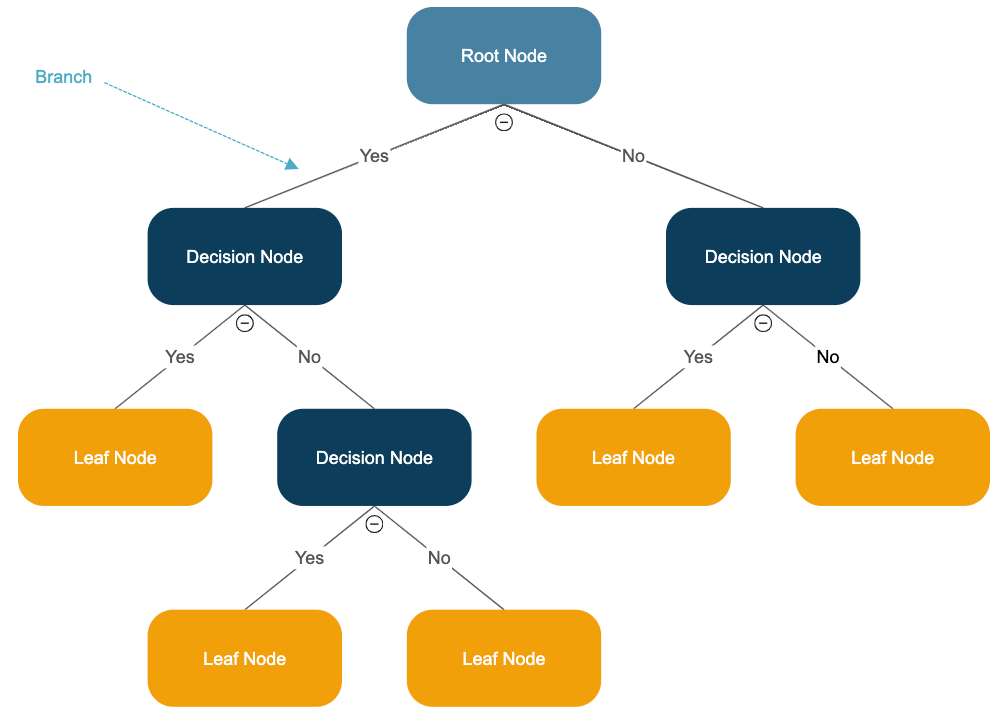
데이터의 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적인 분류가 될 것인가가 알고리즘의 성능을 크게 좌우한다.
Decision node = 규칙 조건, Leaf node = 결정된 클래스 값
❗많은 규칙이 있다 → 분류를 결정하는 방식이 복잡해진다 → 과적합으로 이어지기 쉽다
❗트리의 깊이가 깊어질수록 결정 트리의 예측 성능이 저하될 가능성 ↑
→ 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 Decision node의 규칙이 정해져야 한다
→ 균일한 데이터 세트를 구성할 수 있도록 분할하는 것이 필요
❓균일한 데이터 세트란?
- 데이터를 판단하는 데 있어 상대적으로 더 적은 정보가 필요한, 쉽게 예측할 수 있도록 된 데이터 세트 (e.g. 모두 검은 공)
- 정보 이득(Information Gain) 지수, 지니 계수로 균일도 측정
- 정보 이득 지수가 높거나, 지니 계수가 낮은 조건을 찾아 데이터 세트 분할

1) 결정 트리 모델의 특징

장점
1. 균일도를 기반으로 하고 있어 알고리즘이 쉽고 직관적이다.
2. 피처의 스케일링과 정규화 같은 전처리 작업이 필요 없다.
단점
1. 과적합으로 정확도가 떨어진다.
(트리 깊이가 계속 커지고 결과적으로 복잡한 학습 모델이 됨 → 트리 크기를 사전에 제한하는 것이 도움이 됨)

2) 결정 트리 파라미터

DecisionTreeClassifier : 결정 트리 알고리즘을 구현한, 분류(Classification)를 위한 클래스
- min_samples_split : 노드를 분할하기 위한 최소한의 샘플 데이터 수, 과적합 제어 시 사용됨 (작게 설정 → 분할되는 노드 ↑ → 과적합 가능성 ↑)
- min_samples_leaf : 분할될 경우 왼쪽과 오른쪽 브랜치 노드에서 가져야 할 최소한의 샘플 데이터 수
- max_features : 최적의 분할을 위해 고려할 최대 피처 개수
- max_depth : 트리의 최대 깊이
- max_leaf_nodes : 말단 노드의 최대 개수

3) 결정 트리 모델의 시각화

Graphviz 설치 후 이용
- 브랜치(Branch) 노드: 자식 노드가 있는 노드, 자식 노드를 만들기 위한 분할 규칙 조건을 가지고 있다
- 리프(Leaf) 노드: 자식 노드가 없는 노드, 최종 클래스(레이블)값이 결정된 노드

from sklearn.tree import export_graphviz

export_graphviz(dt_clf, out_file="tree.dot", class_names=iris_data.target_names, 
                feature_names=iris_data.feature_names, impurity=True, filled=True)
                

import graphviz

with open("tree.dot") as f:
    dot_graph = f.read()

graph = graphviz.Source(dot_graph)
graph

# 이미지로 저장
# graph.render(filename='test_img', directory='C:/Users/splen/Desktop', format='png')

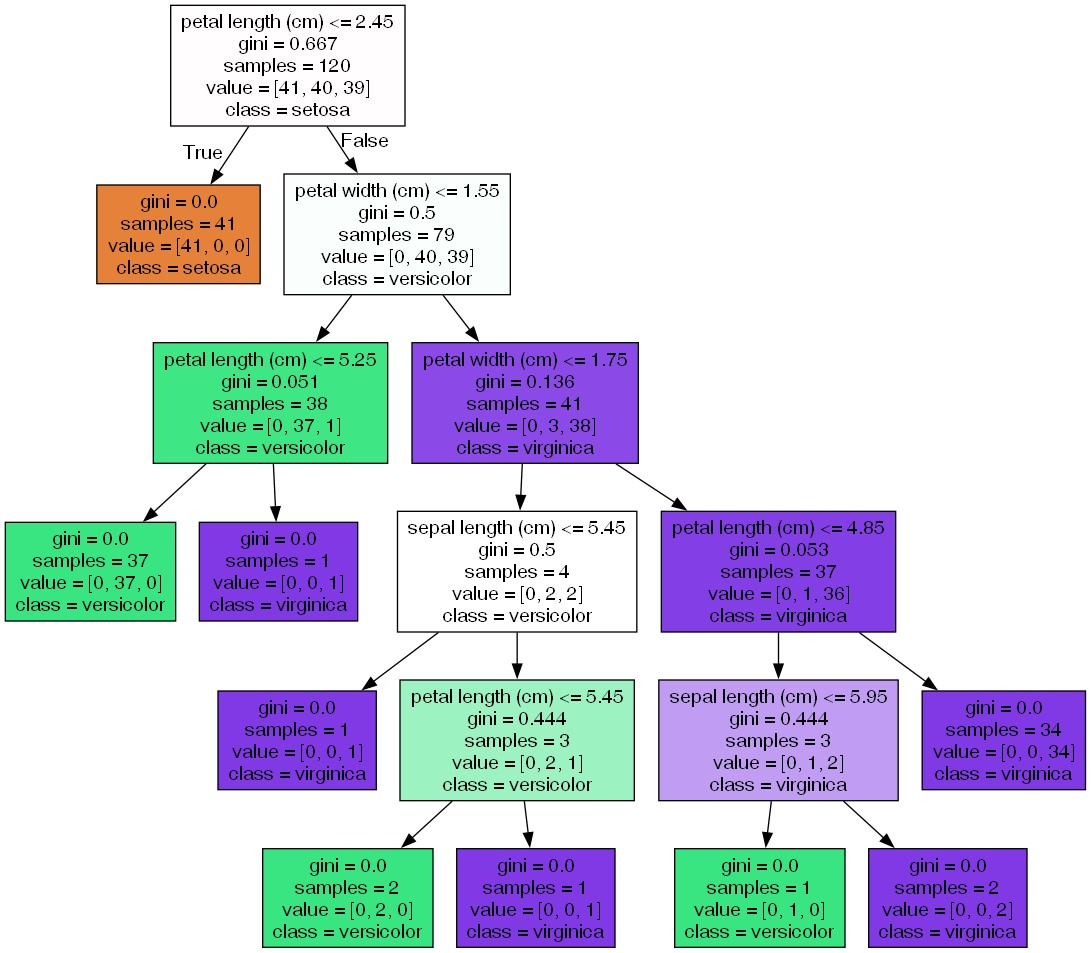
[결과 및 설명]

petal length(cm) <= 2.45 와 같은 피처의 조건: 자식 노드를 만들기 위한 규칙 조건, 이런 조건이 없으면 리프 노드
value = [ ] 는 클래스 값 기반의 데이터 건수, 위의 경우에 label 0/1/2 클래스에 대한 각각의 데이터 개수를 의미
gini : value = [ ]에서 주어진 데이터 분포에서의 지니 계수 (낮으면 좋음)
samples : 현 규칙에 해당하는 데이터 건수
class : 현 데이터에서 가장 많은 건수의 데이터가 속한 클래스, 예측 클래스
각 노드의 색깔은 데이터의 레이블 값 의미
색깔이 짙을수록 지니 계수 ↓, 해당 레이블에 속하는 샘플 데이터 ↑
완벽하게 클래스 값을 구별하기 위해 트리 노드를 계속해서 만들어 나감 → 모델이 쉽게 과적합되는 문제
따라서 결정 트리 알고리즘을 제어하는 대부분의 하이퍼 파라미터는 복잡한 트리가 생성되는 것을 막기 위한 용도이다.

결정트리는 어떠한 속성을 규칙 조건으로 선택하느냐가 중요한 요건이다.
feature_importances_ 로 ndarray 형태로 피처 순서대로 중요도 값을 리턴

4) 결정 트리 과적합 (Overfitting)

Sklearn에서 제공하는 make_classification() 함수: 분류를 위한 테스트용 데이터 쉽게 생성 가능, 호출 시 반환되는 객체는 피처 데이터 세트 & 클래스 레이블 데이터 세트

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
%matplotlib inline

plt.title("3 Class values with 2 features sample data creation")

# 피처 2개, 클래스 3가지 유형의 분류 샘플 데이터 생성
X_features, y_labels = make_classification(n_features=2, n_redundant=0, n_informative=2, n_classes=3,
                                          n_clusters_per_class=1, random_state=0)

# 2개의 피처로 2차원 좌표 시각화, 각 클래스 값은 다른 색깔로 표시
plt.scatter(X_features[:, 0], X_features[:, 1], marker='o', c=y_labels, s=25, edgecolor='k')

[output]

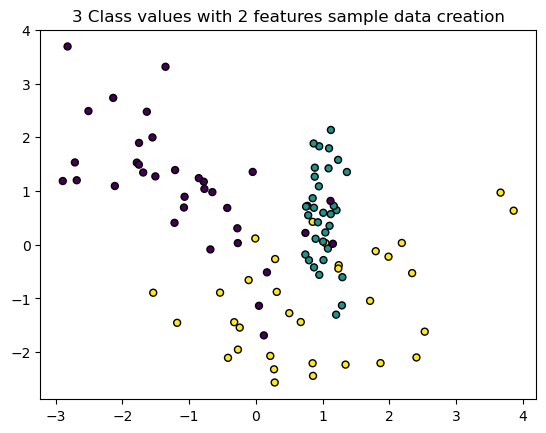
각 피처가 X, Y축으로 나열된 2차원 그래프
3개의 클래스 값 구분은 색깔로 한다.
X_features와 y_labels 데이터 세트를 기반으로 결정트리를 학습시킨다.

[트리 생성 제약 없는 경우]

from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(random_state=156).fit(X_features, y_labels)
visualize_boundary(dt_clf, X_features, y_labels)

[트리 생성 조건 제약한 경우]

# min_samples_leaf=6 으로 트리 생성 조건을 제약한 결정 경계 시각화
dt_clf = DecisionTreeClassifier(min_samples_leaf=6, random_state=156).fit(X_features, y_labels)
visualize_boundary(dt_clf, X_features, y_labels)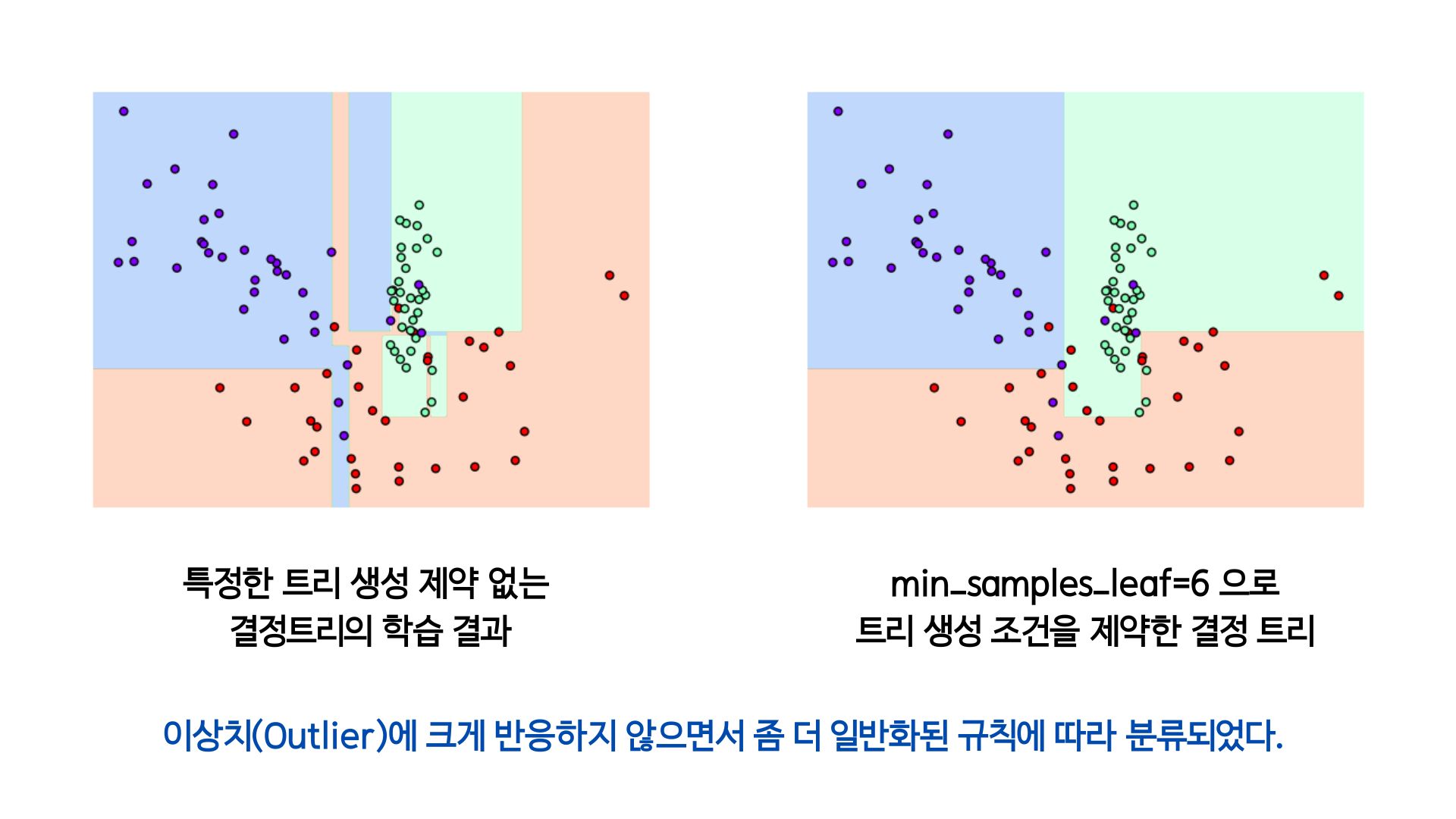

❗이상치(Outlier)란, 보통 관측된 데이터의 범위에서 많이 벗어난 아주 작은 값이나 큰 값을 말한다.

[실습] 사용자 행동 인식 데이터 세트

사용자 행동 인식 데이터 세트
- UCI 머신러닝 리포지토리(Machine Learning Repository) 제공
- 30명에게 스마트폰 센서를 장착시킨 뒤 사람의 동작과 관련된 여러 가지 피처를 수집한 데이터

❗파라미터 vs. 하이퍼파라미터
➡️ 파라미터는 학습의 대상으로, 학습 알고리즘을 통해 자동적으로 학습하게 된다. 하이퍼파라미터는 경험, 데이터의 특성 등에 근거해 사용자가 설정하는 값이다.
Sklearn의 GridSearchCV
- 하이퍼 파라미터 튜닝에 사용
- 하이퍼 파라미터 튜닝: 여러 실험을 통해 하이퍼파라미터 세트를 선택하고 모델을 통해 실행하는 것
- 머신러닝 알고리즘에 사용되는 하이퍼 파라미터를 입력해 학습을 하고 측정을 하면서 가장 좋은 하이퍼 파라미터를 알려주는 역할

from sklearn.model_selection import GridSearchCV

# 최대 깊이 6, 8, ... 로 변화시키면서 예측 성능 확인
params = {
    'max_depth' : [6, 8, 10, 12, 16, 20, 24],
    'min_samples_split' : [16]  # 고정값
}

grid_cv = GridSearchCV(dt_clf, param_grid=params, scoring='accuracy', cv=5, verbose=1)
grid_cv.fit(X_train, y_train)
print('GridSearchCV 최고 평균 정확도 수치: {0:.4f}'.format(grid_cv.best_score_))
print('GridSearchCV 최적 하이퍼 파라미터:', grid_cv.best_params_)

max_depth가 8일 때 5개 폴드 세트의 최고 평균 정확도 결과가 약 85.49%인 것으로 나타난다.

Fitting 5 folds for each of 7 candidates, totalling 35 fits
GridSearchCV 최고 평균 정확도 수치: 0.8549
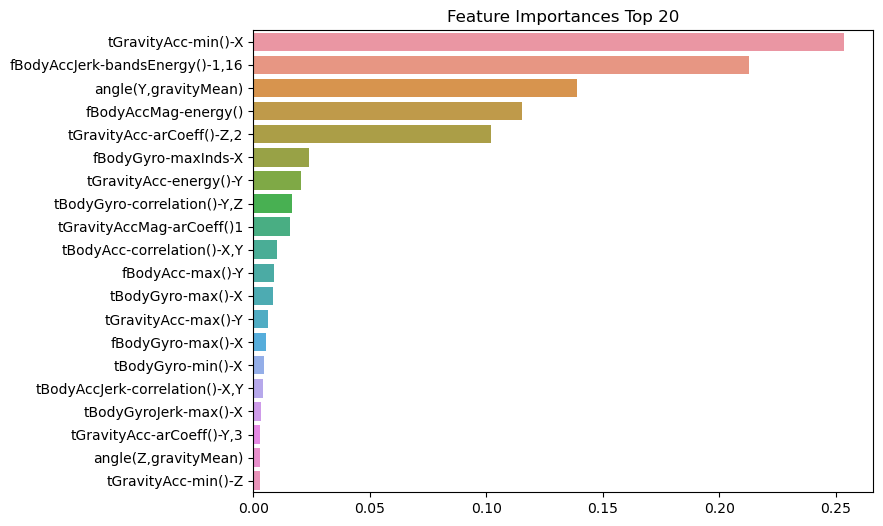
GridSearchCV 최적 하이퍼 파라미터: {'max_depth': 8, 'min_samples_split': 16}

feature_importances_ 이용하여 피처 중요도 확인 & 그래프로 나타내기
→ 중요도가 높은 피처들이 결정 트리의 규칙 생성에 중요한 영향을 미친다.

03. 앙상블 학습 (Ensemble Learning)

: 여러 개의 분류기(Classifier)르 생성하고 그 예측을 결합함으로써 보다 정확한 최종 예측을 도출하는 기법

이미지, 영상, 음성 등의 비정형 데이터의 분류는 딥러닝이 뛰어난 성능을 보이지만, 대부분의 정형 데이터 분류에서 뛰어난 성능을 보인다.
앙상블 학습의 유형
하드 보팅: 다수의 분류기 간 다수결로 최종 클래스 결정
소프트 보팅: 분류기들의 레이블 값 결정 확률을 모두 더하고 이를 평균해서 이들 중 확률이 가장 높은 레이블 값을 최종 보팅 결과값으로 선정
(일반적인 보팅 방법)
보팅 분류기 (Voting Classifier)
- Sklearn에서 보팅 방식의 앙상블을 구현한 VotingClassifier 클래스 제공

lr_clf = LogisticRegression(solver='liblinear')
knn_clf = KNeighborsClassifier(n_neighbors=8)

vo_clf = VotingClassifier(estimators=[('LR', lr_clf), ('KNN', knn_clf)], voting='soft')

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.2, random_state=156)

# VotingClassifier 학습, 예측, 평가
vo_clf.fit(X_train, y_train)
pred = vo_clf.predict(X_test)
print('Voting 분류기 정확도: {0:.4f}'.format(accuracy_score(y_test, pred)))

# 개별 모델 학습, 예측, 평가
classifiers = [lr_clf, knn_clf]
for classifier in classifiers:
    classifier.fit(X_train, y_train)
    pred = classifier.predict(X_test)
    class_name = classifier.__class__.__name__
    print('{0} 정확도: {1:.4f}'.format(class_name, accuracy_score(y_test, pred)))

04. 랜덤 포레스트

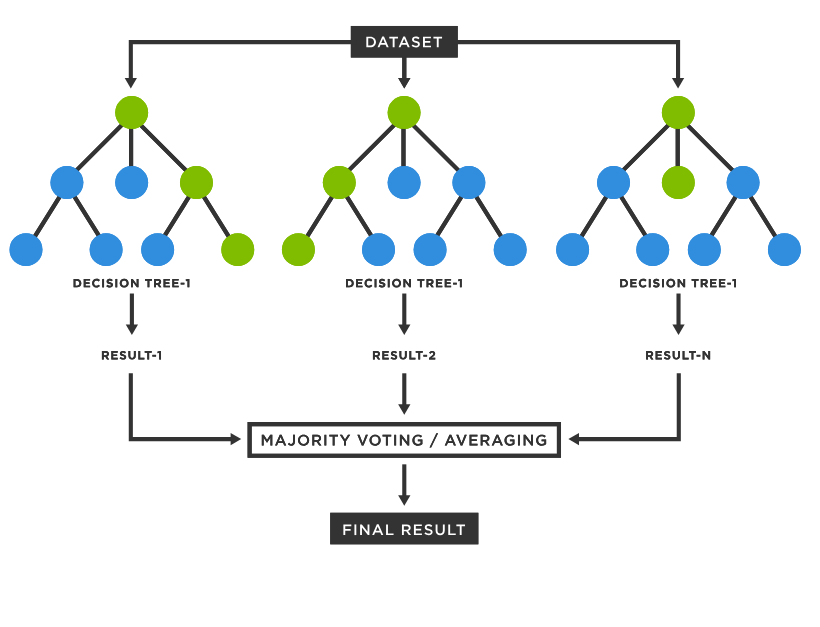
배깅의 대표적인 알고리즘
여러 개의 결정 트리 분류기가 전체 데이터에서 배깅 방식으로 각자의 데이터를 샘플링해 개별적으로 학습을 수행한 뒤, 최종적으로 모든 분류기가 보팅을 통해 예측 결정을 하게 된다.
부트스트래핑(Bootstraping) 분할 방식: 개별 트리가 학습하는 데이터 세트는 전체 데이터에서 일부가 중첩되게 샘플링된 데이터 세트이다.
Sklearn에서 RandomForestClassifier 제공

랜덤 포레스트 하이퍼 파라미터 튜닝

트리 기반 앙상블 알고리즘의 단점 중 하나는 하이퍼 파라미터가 너무 낳고 그로 인해 튜닝을 위한 시간이 많이 소모된다는 것이다.
랜덤 포레스트 하이퍼 파라미터
- n_estimators : 결정 트리 개수
- max_features, max_depth, min_samples_leaf, min_samples_split와 같은 결정 트리 파라미터와 똑같이 적용
GridSearchCV 로 랜덤 포레스트의 하이퍼 파라미터 튜닝을 할 수 있다.