[백준] 파일 합치기 (Kotlin)

문제 바로가기

해당 문제는 DP로 해결해야하는 문제이다.
아직까지도 DP문제를 마주치면 두려움이 엄습해오는데, 꾸준히 공부하고 기록하며 DP에 대한 두려움을 극복하고자 한다.

문제

소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠 때 필요한 비용(시간 등)이 두 파일 크기의 합이라고 가정할 때, 최종적인 한 개의 파일을 완성하는데 필요한 비용의 총 합을 계산하시오.

예를 들어, C1, C2, C3, C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 각각 40, 30, 30, 50 이라고 하자. 이 파일들을 합치는 과정에서, 먼저 C2와 C3를 합쳐서 임시파일 X1을 만든다. 이때 비용 60이 필요하다. 그 다음으로 C1과 X1을 합쳐 임시파일 X2를 만들면 비용 100이 필요하다. 최종적으로 X2와 C4를 합쳐 최종파일을 만들면 비용 150이 필요하다. 따라서, 최종의 한 파일을 만드는데 필요한 비용의 합은 60+100+150=310 이다. 다른 방법으로 파일을 합치면 비용을 줄일 수 있다. 먼저 C1과 C2를 합쳐 임시파일 Y1을 만들고, C3와 C4를 합쳐 임시파일 Y2를 만들고, 최종적으로 Y1과 Y2를 합쳐 최종파일을 만들 수 있다. 이때 필요한 총 비용은 70+80+150=300 이다.

소설의 각 장들이 수록되어 있는 파일의 크기가 주어졌을 때, 이 파일들을 하나의 파일로 합칠 때 필요한 최소비용을 계산하는 프로그램을 작성하시오.

입력

프로그램은 표준 입력에서 입력 데이터를 받는다. 프로그램의 입력은 T개의 테스트 데이터로 이루어져 있는데, T는 입력의 맨 첫 줄에 주어진다.각 테스트 데이터는 두 개의 행으로 주어지는데, 첫 행에는 소설을 구성하는 장의 수를 나타내는 양의 정수 K (3 ≤ K ≤ 500)가 주어진다. 두 번째 행에는 1장부터 K장까지 수록한 파일의 크기를 나타내는 양의 정수 K개가 주어진다. 파일의 크기는 10,000을 초과하지 않는다.

출력

프로그램은 표준 출력에 출력한다. 각 테스트 데이터마다 정확히 한 행에 출력하는데, 모든 장을 합치는데 필요한 최소비용을 출력한다.

예제 입력

2
4
40 30 30 50
15
1 21 3 4 5 35 5 4 3 5 98 21 14 17 32

예제 출력

300
864

접근 방법

우선 이 문제를 왜 DP로 접근해야하는가? 부터 생각해보자. 비용의 합을 구하는 과정에서 첫 번째, 두 번째 케이스 모두 150이라는 C1~C4의 전체 비용 합을 더해주는 연산이 중복해서 나타난다. 어떠한 문제의 SubProblem이 중복해서 나타난다면, 이 문제는 DP로 푸는 것이 적절해보인다. 중복하지 않는다면? -> 분할정복으로 접근하면 된다.

그렇다면, 이 문제의 dp 배열이 과연 1차원 배열일까 아니면 2차원 배열일까를 또 고민해봐야 한다. 결국 연속된 파일들을 특정한 구간 내에서 여러 합쳐서 누적합을 구하는 과정이 하나의 SubProblem이 되는 것이고, 이 모든 SubProblem들이 합쳐져서 큰 전체의 문제를 해결하는 것이다. 그럼 dp 배열은 결국 x~y번째 파일들을 합치는데 필요한 최소비용이 되는 것이고, 시작하는 인덱스 x, 끝나는 인덱스 y 2가지의 파라미터가 필요하므로 dp 배열은 2차원 배열이 되어야 한다.

그래서 결국 dp[x][y]는 x번째부터 y번째 파일들을 합치는데 필요한 최소비용(누적 합)이다.
또한 전체 비용 합이 중복해서 나타나기 때문에 sum[x] 라는 1번째 부터 x번째 파일까지의 비용을 총 합한 배열이 추가적으로 필요하다.

그림을 통해 추가적으로 설명해보겠다.

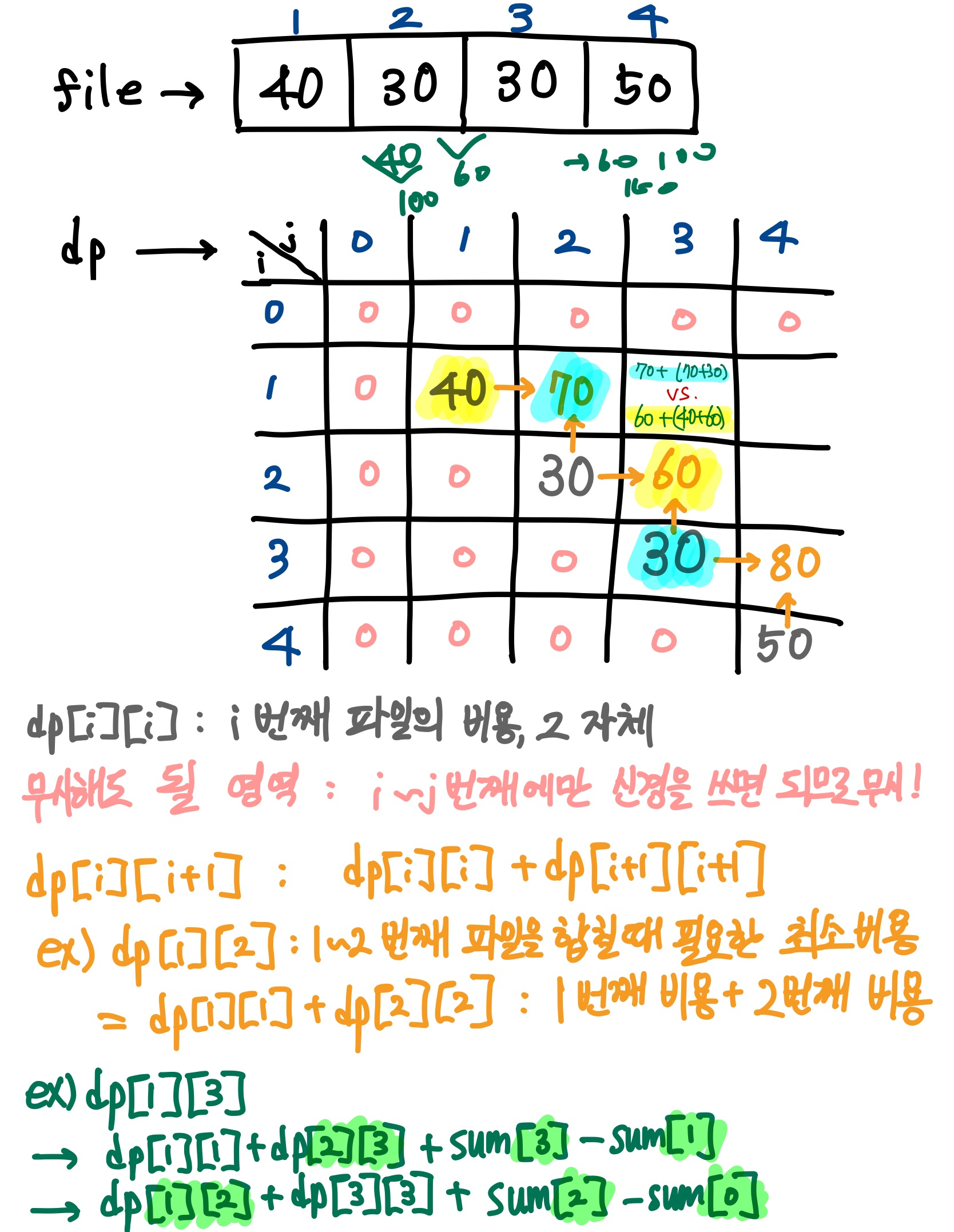
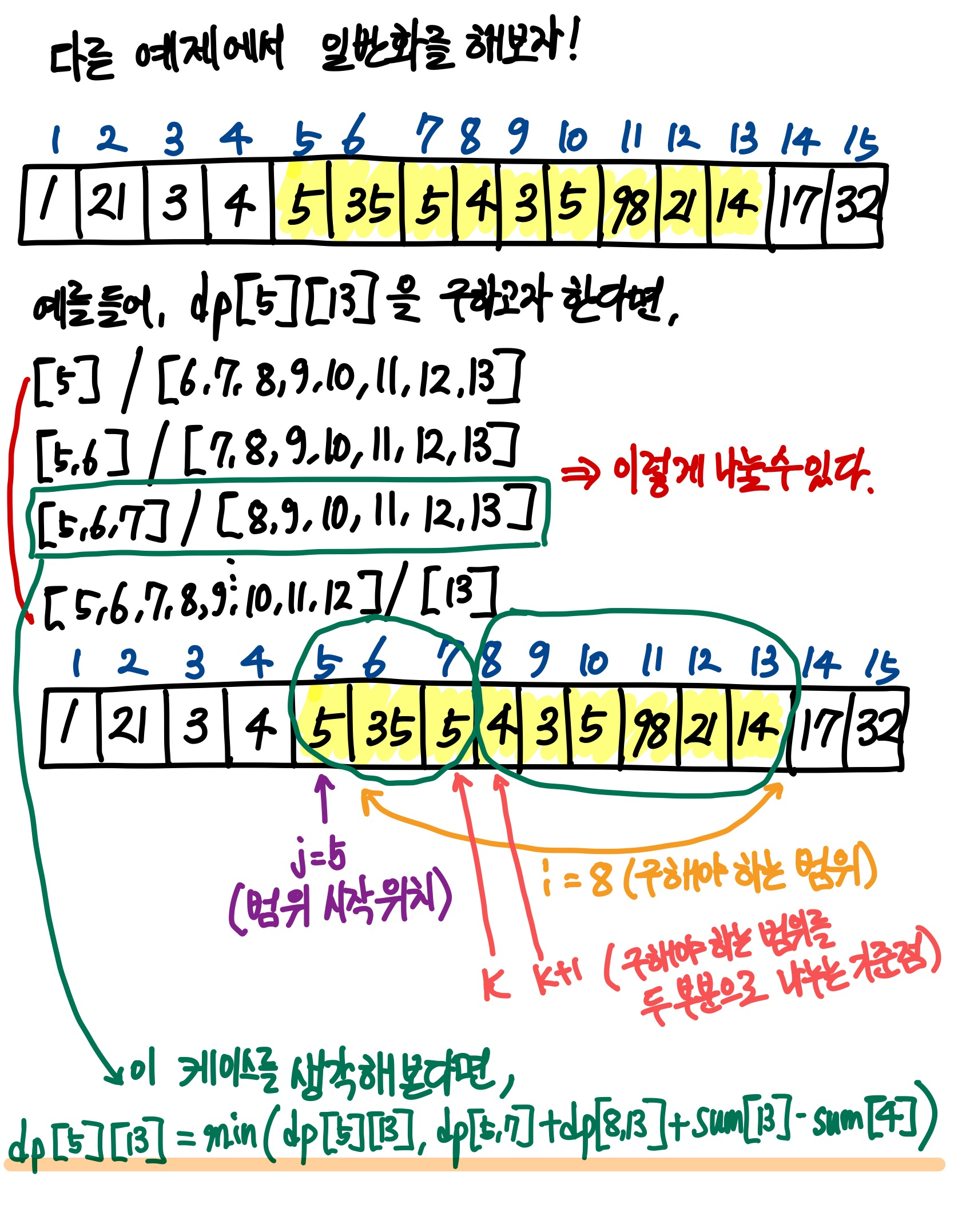
결국 플이 코드는 삼중 for문으로 돌아가며, O(N³)의 시간 복잡도를 가지게 된다.

처음에는 이게 맞나 싶었지만, K가 최대 500이므로 500^3 = 대략 1억 2천 5백만번의 연산을 시간 제한 2초내에 수행할 수 있을 것 같아 그대로 코드를 짜보았다.

설명을 덧붙이자면, 구해야 하는 범위 크기인 i가 1일 때는 1~2번째 파일, 2~3번째 파일, 3~4번째 파일, ... 이고 i가 2일 때는 1~3번째 파일, 2~4번째 파일, 3~5번째 파일, ... 이다.

풀이 코드 (kotlin)

fun main() {
    val t = readln().toInt()
    repeat(t) {
        val K = readln().toInt()
        val files = readln().split(" ").map { it.toLong() }
        val dp: Array<LongArray> = Array(K + 1) { LongArray(K + 1) }
        val sum = LongArray(K + 1)

        // sum 배열 초기화
        for (i in 1..K) {
            sum[i] = sum[i - 1] + files[i - 1]
        }

        // bottom-up 방식으로 dp 배열 채워나가기
        for (i in 1..K) {
            for (j in 1..K - i) {
                dp[j][j + i] = MAX_VALUE
                for (k in j until j + i) {
                    dp[j][j + i] = min(dp[j][j + i], dp[j][k] + dp[k + 1][j + i] + sum[j + i] - sum[j - 1])
                }
            }
        }

        // 1~k번쨰 까지 파일들을 합치는데 필요한 최소비용 출력
        println(dp[1][K])
    }
}

결과!!!