인공신경은 노드(unit)와 엣지(connection)로 이루어져있다.

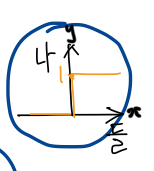
이게 노드.

우리가 흔히 x, y축이라고 하는게 사실 x축은 들어가는 거(= input), y축은 나오는거(= output) 라고 볼 수 있다.

• 웨이트(중요도)를 곱하고 바이어스(민감도)와 함께 더하고, activation
• 주어진 입력에 대해 원하는 출력이 나오도록 웨이트, 바이어스를 AI가 알아내는 것. 이게 바로 “AI가 학습을 한다”라는 것.
• 근데, AI가 스스로 적절한 웨이트, 바이어스를 알아낸다.

인공신경망

• 곱하고 더하고 activation, 곱하고 더하고 activation… 이게 반복. 인공신경이 반복되는 것.
• 모든 노드들이 연결되어있는 신경망을 multi layer perceptron (MLP)라고 한다.
  • 사실 perceptron은 unit step function을 활성화 함수로 사용하는 인공 신경을 의미하지만, MLP는 임의의 활성화 함수를 사용하는 인공 신경망을 의미한다.

Input layer & output layer (& hidden layer)

• 깊은 인공신경망은 Deep Neural Network로 예전 기준에는 은닉층이 3개만 되도 깊다고 할 수 있는데 요즘에는 컴퓨터 성능이 워낙 뛰어나서 100층 이상인것도 많다.
• 참고로 노드끼리 싹다 연결한 층은 FC(fully-connected) layer라고 한다.

다시 말하면, 주어진 입력에 대해 원하는 출력이 나오도록 하는 함수를 만들자는 것
→ 인공신경망은 함수다!!

그럼 $ax+b$ (일차함수)를 인공 신경망으로 표현해보자

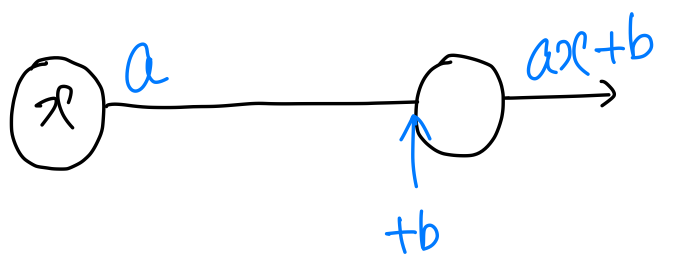
x 노드가 존재하고 가중치 a 와 바이어스 b 가 있고, 결과로 $ax+b$가 출력이 된다.

선형 회귀

• 입력과 출력 간의 (선형)관계를 파악하는 것 = 회귀
  → 처음 보는 입력에 대해서도 적합한 출력을 얻어야 한다.

ex) 키와 몸무게의 (선형)관계를 파악해서 → 처음보는 키에 대해서도 적합한 몸무게를 출력하는 머신을 만들어보자.

그러기 위해선 적절한 a, b를 찾아야 한다.

그렇다면 적절하다는 건 뭘까?

• loss(=cost)를 최소화 하는 것이 적절한 weight
• 머신의 출력 (예측 $\hat{y}$)과 나와야할 출력(정답 $y$)의 차이로 loss를 정의해보자.
• 다양한 loss 함수 중 MSE(Mean Squared Error)라는 걸 써보자.
  • MAE(mean absolute error)도 있는데, 절댓값보다 제곱함수가 더 민감하게 반응
    (민감 = x끼리의 차이가 크다면 y가 더 큰 차이가 남)
• L을 최소화하는 weight 어떻게 찾지?
  → a,b를 일일히 바꿔가며 L 값을 그래프로 그려보자
  
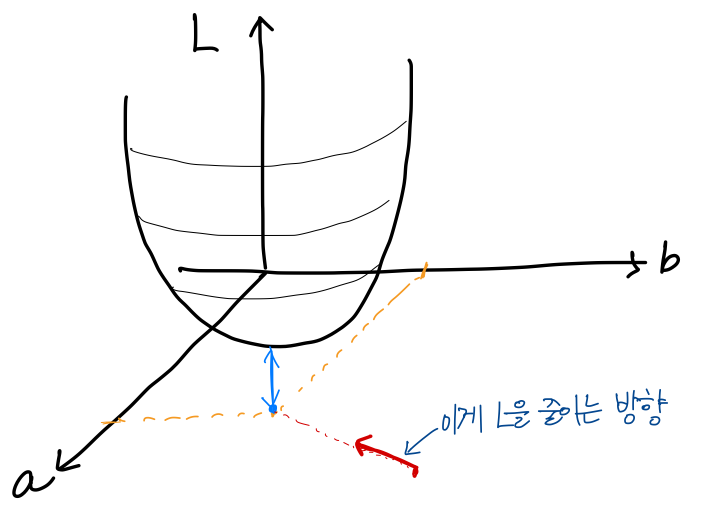
  loss function을 그려보면 위와 같다. 파란색이 loss가 최소가 되는 지점이다.
  무작위로 a, b를 정해서 L이 최소가 되는 방향으로 나아가야 한다.

Gradient Descent

위에서 L이 최소가 되는 방향을 찾는 방법이 경사하강 Gradient descent이다.

• Gradient(편미분을 벡터로 쌓은 것)은 항상 가장 가파른 방향을 향한다.

그럼 그냥 반대 방향으로 가면 되는거 아닐까?

• 단순히 반대 방향으로 가면 최적화 문제가 발생한다.
• 과적합, local minima, 계산 비용 의 문제가 생김. (나중에 배움)
• 위의 이유로 학습률이라는 파라미터가 있는거다.

  그래디언트 디센트는 '학습률(learning rate)'이라는 하이퍼파라미터를 도입합니다. 학습률은 그래디언트 방향으로 얼마나 큰 걸음을 걸을지 결정합니다. 이를 통해 알고리즘은 점진적으로, 그리고 안정적으로 최솟값에 접근할 수 있게 됩니다.
  또한, Adam, RMSprop, Adagrad 등의 발전된 최적화 알고리즘들은 이러한 문제들을 더욱 효과적으로 다루기 위해 학습률을 동적으로 조정하거나, 그래디언트의 역사를 활용하는 등의 추가적인 테크닉을 사용합니다.
  결론적으로, 그래디언트 디센트에서 '반대 방향으로 가는 것'은 맞지만, '얼마나 갈 것인가'를 신중하게 결정하는 것이 알고리즘의 핵심입니다. 이는 최적화 과정을 안정적이고 효율적으로 만들어, 복잡한 손실 함수 지형에서도 성공적으로 최솟값을 찾을 수 있게 해줍니다.

learning rate의 존재 이유

위에는 lr이 클 때만 설명했는데, lr이 너무 작아도 너무 천천히 가서 문제가 생김.

Initial weight

1. initial weight의 중요성
   • L을 최소로 만드는 여행을 떠난다고 할 때 출발지를 어디로 정할지가 중요하다.
     어디서 출발하느냐에 따라 목적지에 도착하는 경로가 완전히 달라질 수 있다.
     좋은 출발점은 빠르고 효율적으로 목적지로 안내할 수 있따.
   • 수렴속도와 안정성
     • 적절한 속도와 올바른 방향으로 시작하면, 목적지까지 빠르고 안전하게 갈 수 있다.
     • 좋은 초기 가중치는 학습을 빠르고 안정적으로 만들어준다.
   • local minima 회피
   • gradient loss , explode 방지
2. Weight Initialization 종류
   ($N_{in}$ = 입력 뉴련의 수, $N_{out}$ = 출력 뉴런의 수)

• Lecun $w \sim U(-\sqrt{\frac{3}{N_{in}}}, \sqrt{\frac{3}{N_{in}}})$ or $w \sim N(0, \frac{1}{N_{in}})$
  
• Xavier (sigmoid / tanh 사용하는 신경망) $w \sim U(-\sqrt{{\frac{6}{N_{in} + N_{out}}}}, \sqrt{{\frac{6}{N_{in} + N_{out}}}})$ or $w \sim N(0, \frac{2}{N_{in} + N_{out}})$
  
• He (ReLU 사용하는 신경망) $w \sim U(-\sqrt{\frac{6}{N_{in}}}, \sqrt{\frac{6}{N_{in}}})$ or $w \sim N(0,\frac{2}{N_{in}})$
  

극단적인 초기화 방법의 영향
1. 모든 가중치를 0으로 초기화할 경우

• 모든 뉴런이 동일한 출력을 생성하게 됩니다.
• 역전파 과정에서 모든 가중치가 동일하게 업데이트되어 네트워크가 제대로 학습할 수 없습니다.
• 대칭성 문제 라고 불림

2. 모든 가중치를 1로 초기화할 경우

• 활성화 함수에 따라 다른 문제가 발생한다.
  • sigmoid, tanh → saturation(포화) 상태에 빠져 그래디언트가 소실될 수 있습니다.
  • ReLU → 그래디언트 폭발이 일어날 수 있다.
• 역전파 과정에서 그래디언트가 제대로 흐르지 않아 학습이 어려워진다.

Stochastic Gradient descent

GD는 모든 데이터를 고려해서 너무 신중해서 문제가 발생했다.
이걸 해결하려고 만든게 SGD

• 랜덤하게 데이터 하나씩 뽑아서 loss를 만듬 (랜덤이라 stochastic)
• → 데이터 하나만 보고 빠르게 방향 결정
  
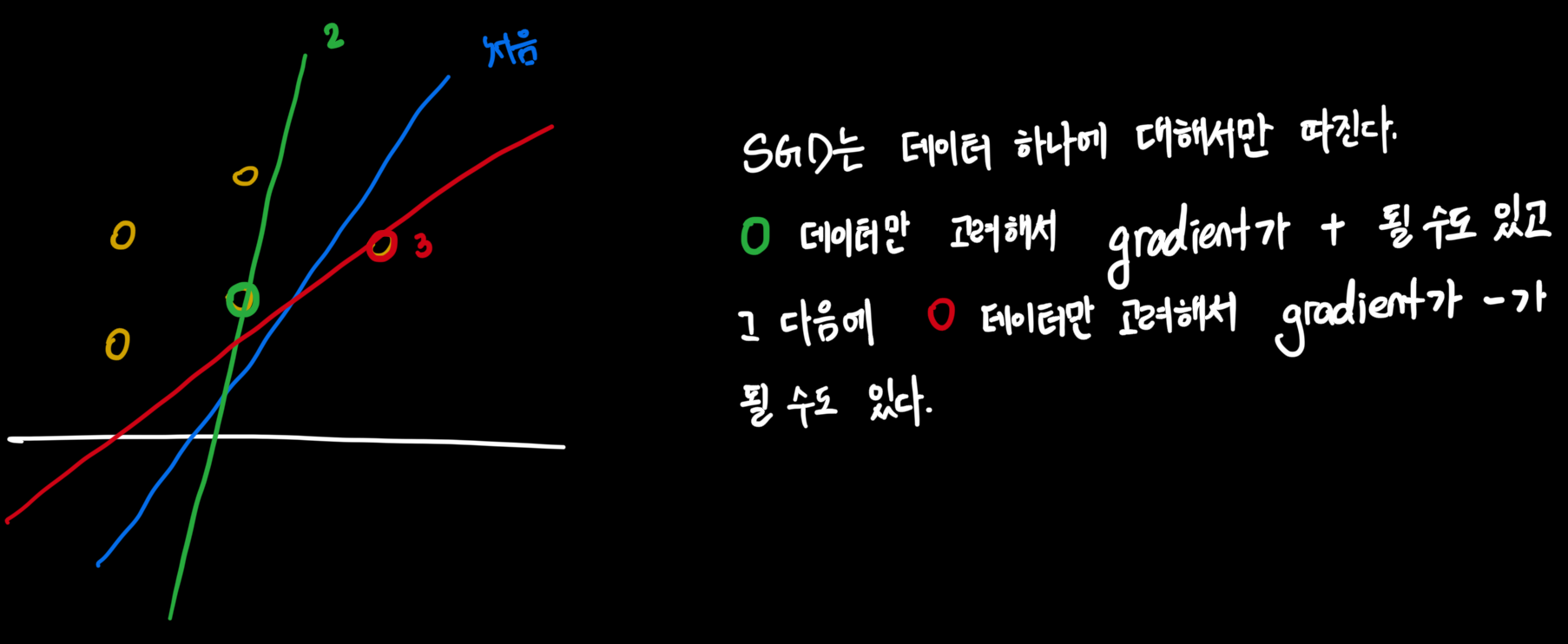
• 비복원추출 방식 , 데이터 다 이용하고 다시 주머니에 넣고 반복
• local minima 로 부터 탈출의 기회가 되기도...

mini-batch SGD

• SGD는 하나씩만 보니까 너무 성급하게 방향 결정 (= 불필요한 움직임이 많다)
  → 마침 GPU로 여러 데이터 동시 통과시킬 수 있기도 하니까 mini-batch를 만들자
• GPU가 허락하는 한 최대한 키우자.
  데이터크기 >> batch size 라서 그게 좋을 듯 하다.
  (다만, 최근의 논문에서는 batch size가 커지는 만큼 learning rate도 같이 키우라는 연구가 있다.)

parameter vs hyperparameter

• 파라미터 (머신이 스스로 알아내는 변수)
  • weights
  • bias (이거도 weight라고 부르기도 함)
• 하이퍼파라미터 (내가 정해줘야 하는 변수)
  • Epoch, batch size
  • learning rate
  • model architecture

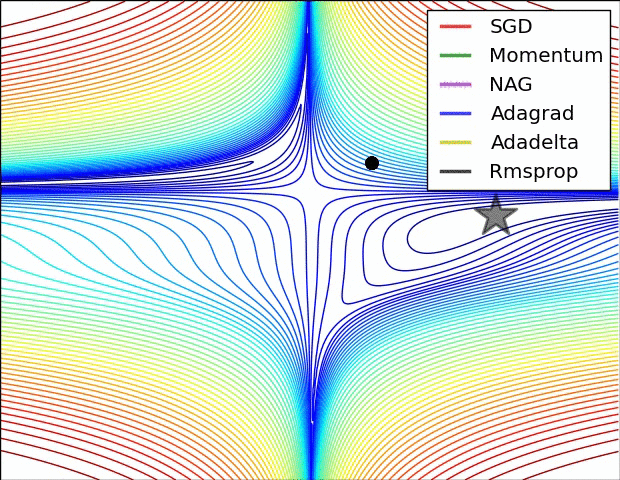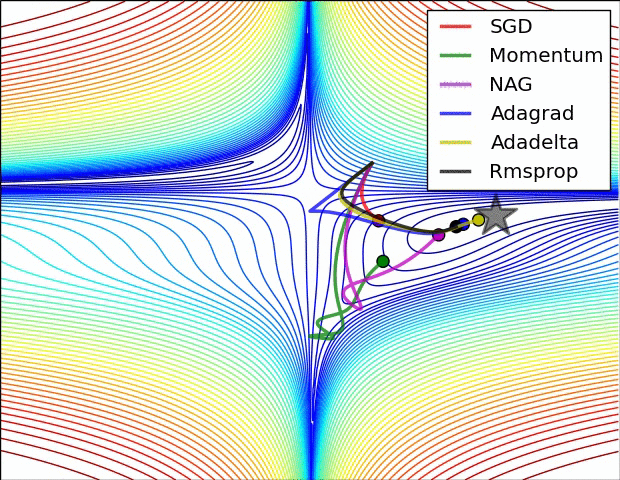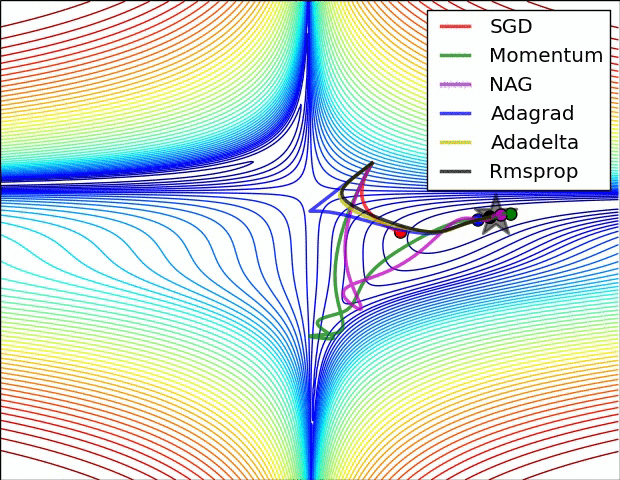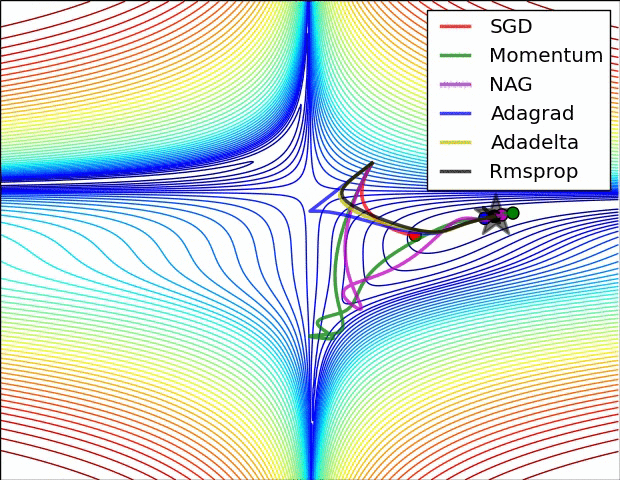
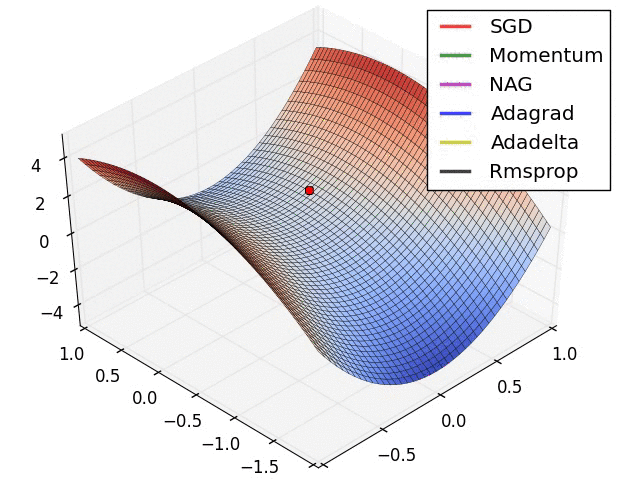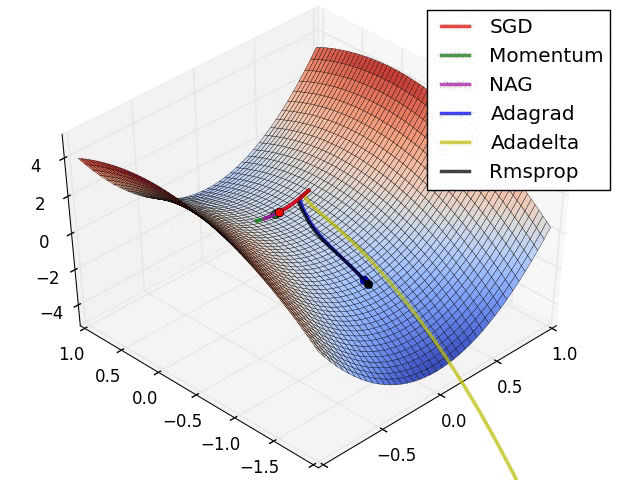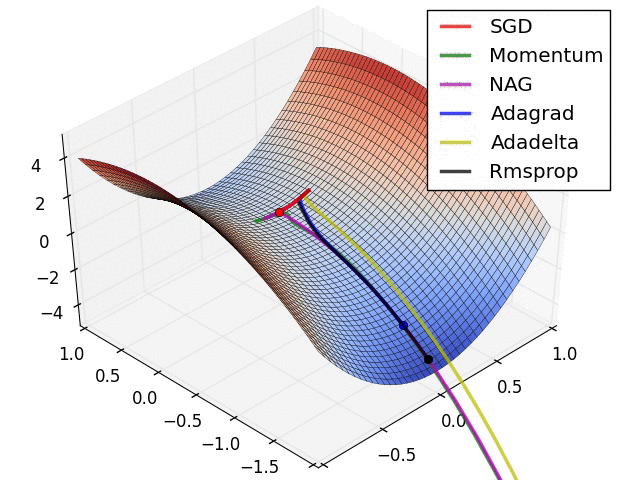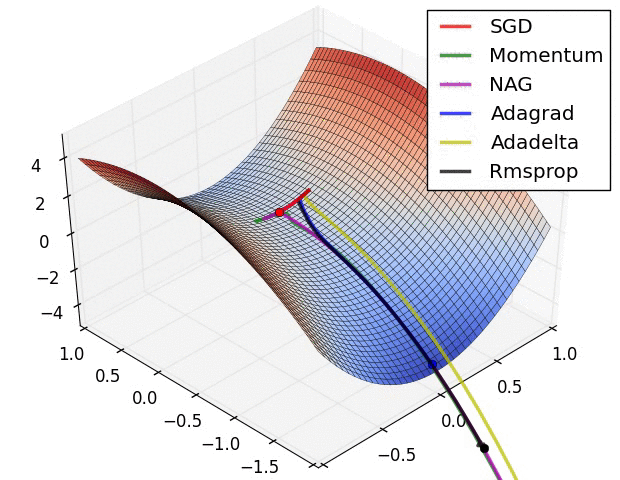
reference: https://www.ruder.io/optimizing-gradient-descent/

K-Fold Cross Validation

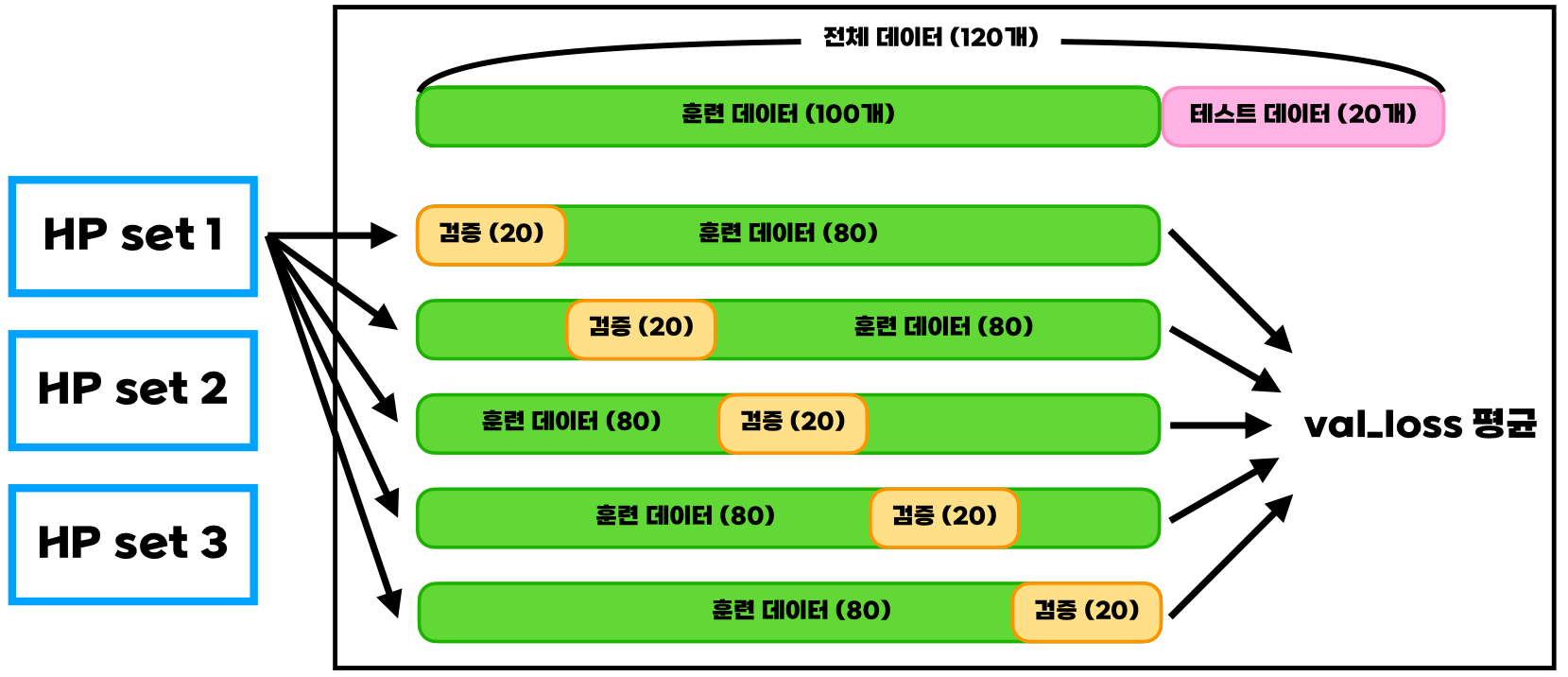
• training data 가 적어서 일부를 validation으로 쓰기 곤란할 때
• 똑같은 하이퍼파라미터를 가진 모델의 파라미터를 각기 다른 train, validation 조합의 데이터로 학습하자는 아이디어 (편향된 validation 데이터를 피함)
• 가장 val loss 평균이 작은 hyperparameter set을 골라, 선택된 set으로 training data 전체에 대해서 새롭게 학습시키거나,
• 학습했던 5개 모델의 출력 결과를 하나로 합치기도 함 (ex. majority vote)