딥러닝과 오버피팅 문제

• 일반적으로 딥러닝이 아닌 신경망보다 "많은 파라미터" 를 가진다.
  -> 필연적으로 학습과정에서 새로운 문제들이 생김.

  오버피팅

  낮은 Bias 높은 Variance

  • 딥러닝은 기본적으로 weight를 깊게 쌓기 쉬운 모델이다. 즉 complexity가 높아져 overfitting이 생기기 쉽다!
    -> 모델이 train data에는 잘 작동하나, test data에는 잘 작동하지 않는다!
    -> 모델 수용량(capacity)가 커지면, 모델이 그만큼 데이터를 더 필요로 하게 된다!
    

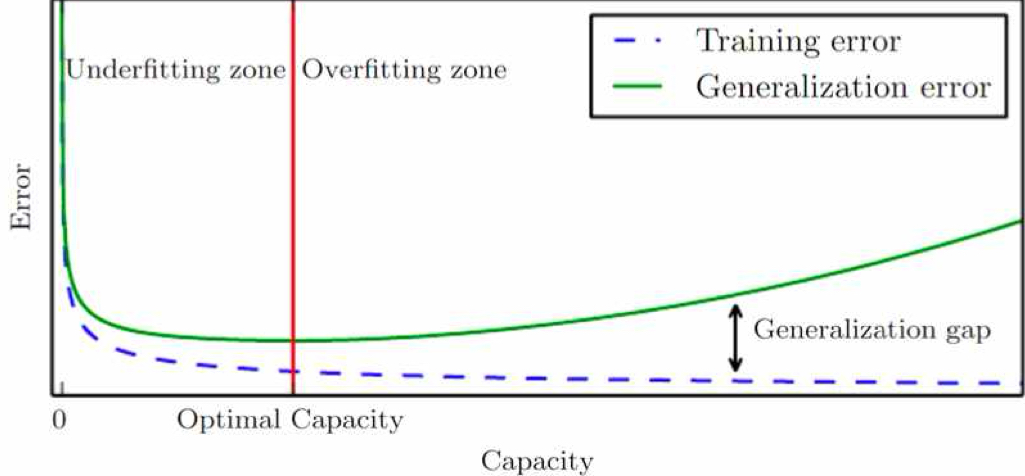
  • 추정 값의 편향 (bias)

    • 모델의 예측 값들의 평균과 이상적인 모델의 예측 값(혹은 실제 값의 평균)과의 차이.
    • $h(x)$를 모델, $f(x)$를 실제 이상적인 예측 함수라고 하면,
      $Bias[h(x)] = E[h(x)] - f(x)$

  • 추정 값의 분산 (Variance)

    • 모델의 예측 값과 모델의 예측 값들의 평균 사이의 차이.
      $Var[h(x)] = E[(h(x) - E[h(x)])^2$

  • 노이즈 (Noise)

    • 실제 값과 이상적인 모델간의 차이(줄일 수 없는 에러)
      $Noise[h(x)] = E[y- f(x))^2] = E[(\theta)^2] = \sigma^2$

• Bias-Variance trade-off
  • 모델의 오류는 다음 식을 만족
    $E[(y-h(x))^2] = E[(h(x)-E[h(x)])^2] + (E[h(x)]-f(x))^2 + E[(y-f(x))^2]$
    
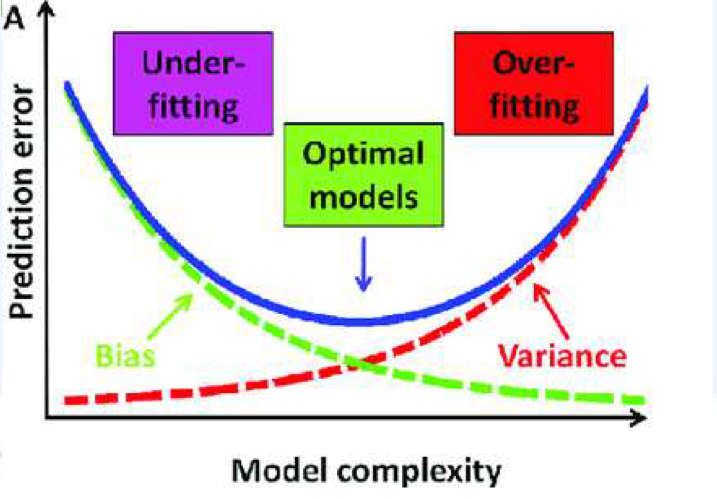
  • Bias, Variance 모두 적절한 단계로 낮은, 모델 수용량을 찾는 것을 목표로 하여야 한다.
  • 그러나, 현식적으로 어려움이 있음
  • 모델 수용량을 올리되, 다른 방법으로 조절 하는게 정형화(Regularization)

정형화 (Regularization)

• 오버피팅이나, well-posesd 문제가 되지 못하고 ill-posed가 된 머신러닝 모델을 추가적인 정보를 더하는 등 프로세스를 통해 해결하는 방법.

  Well-posed 문제란?

  • 존재(exists)하고, 유일(unique)하며, 지속적으로 데이터를 신뢰(depends on data continuously)할 수 있는 문제.

정형화 (Regularization)의 종류는?

• 제한 (restriction)을 거는 파라미터 값 등을 넣는 방법.
• 학습 데이터를 설명하는 여러 개의 가설 모델들을 혼합하는 방법.
• 최적화 프로세스를 수정하는 방법.
• 데이터 분포의 이전 정보(prior knowledge)를 이용하여 추가적인 학습데이터를 더해, 모델 학습에 정형화하는 방법.

3. 앙상블 (Ensemble)

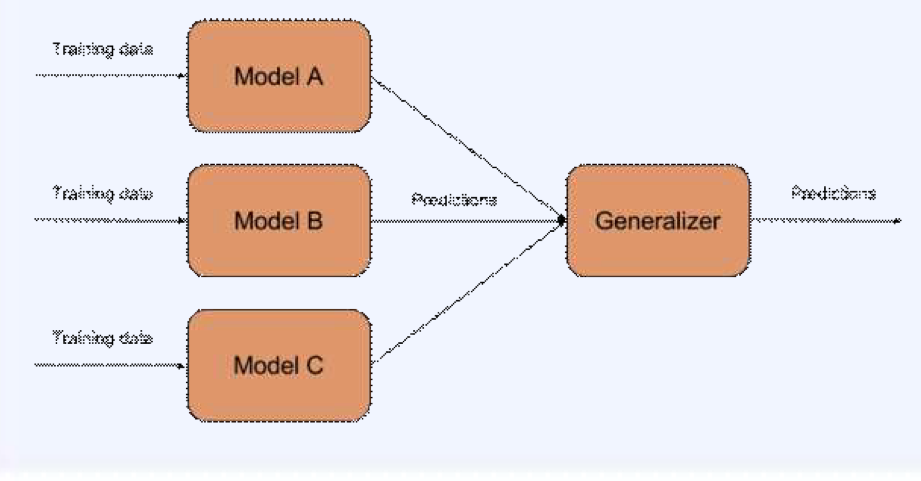
• 여러 개의 가설 모델들을 하나로 합쳐 결과를 얻는다
  단 하나의 모델을 학습할 때 보다, 정확도나 단순모델보다 정확도가 상승할 것이다.
• 왼쪽에서 각 모델이 독립적이라 가정하고, 각 모델의 정확도(accuracy)가 80%라고 해보자.
• 그러면, 각 모델의 결과를 다수결에 따라(Voting) 하나의 결과로 종합했을 때, 전체 모델의 정확도는
  $(0.8)^3 + 3 * (0.8)^2 * 0.2 = 0.896$ 이 나온다.
• 모델의 갯수가 늘어난다면 정확도는 더욱 더 높아진다.

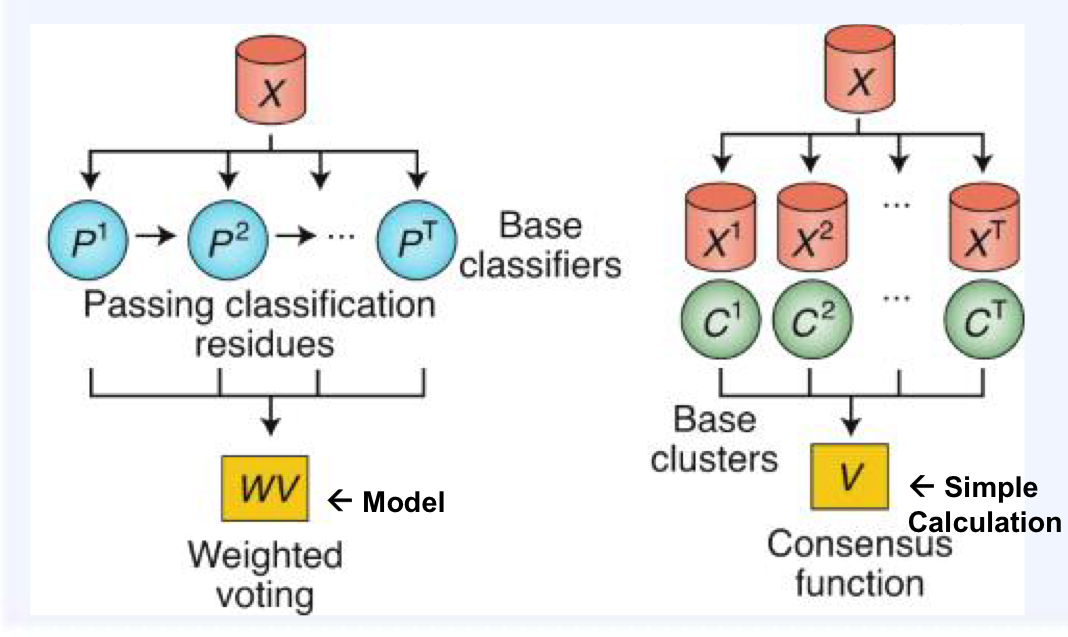
1. 학습(learning)에 의한 결합방식 (왼쪽)

• Boosting
• Bayesian model averaging
• Stacking

2. 동의(consensun)에 의한 결합 방식 (오른쪽)

• Bagging
• Random Forest
• Average of model outputs

Bagging

• n개 데이터 샘플이 주어지고, 학습 모델의 class가 주어졌을 때, m개의 모델을 다른 샘플(bootstrap)로 학습하고, 그것을 aggregating하여 평균화한다.
• 오버피팅 방지에 도움을 준다.
• Variance을 줄인다.
• 독립적인(parallel하게 연산가능한) 모델을 사용한다.

→ 정형화 효과

Boosting

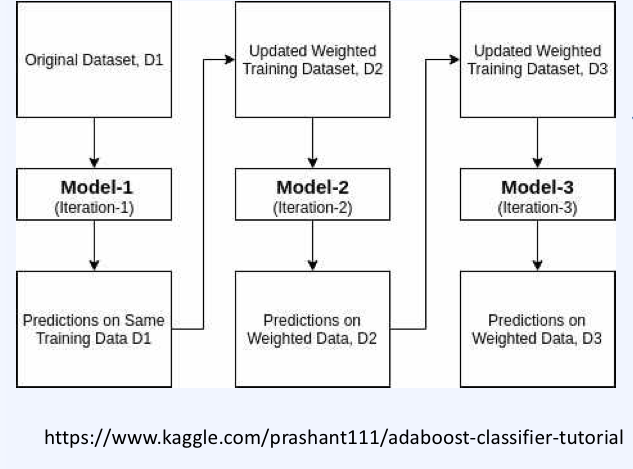
• 성능이 약한 모델을을 순차적(sequential)으로 학습하여 강한 모델들을 만드는 과정.

Ada(adaptive)Boosting

→ 반복적으로, sequential하게 아래 작업을 반복한다.
1. Train dataset을 샘플링한 새로운 dataset을 만든다. 그리고 이 dataset으로 model을 학습시킨다.
2. 학습시킨 모델을 validation한다.
3. Validation 과정에서 잘못 예측한 데이터를 Train dataset에 추가하고 새로운 dataset을 샘플링한다. 즉, 오류 데이터에 가중치를 부여하여 샘플링 될 때 더 잘 뽑히게 만들고 새 모델의 학습을 진행한다.
4. 모델이 2개 이상이 되었으므로 이를 Voting하여 하나의 예측 값으로 하고, 다시 가중치를 계산하여 샘플링이 잘되게 만든다.

Gradient Boosting(XGB)

→ 마찬가지로 아래의 작업을 순차적으로 진행한다.
각 step에서 손실(loss)함수를 계산하고, 각 과정에서 예측값을 이용해 손실(Loss)값의 gradient(미분 값)를 계산하여 최적화한다.

Stacking

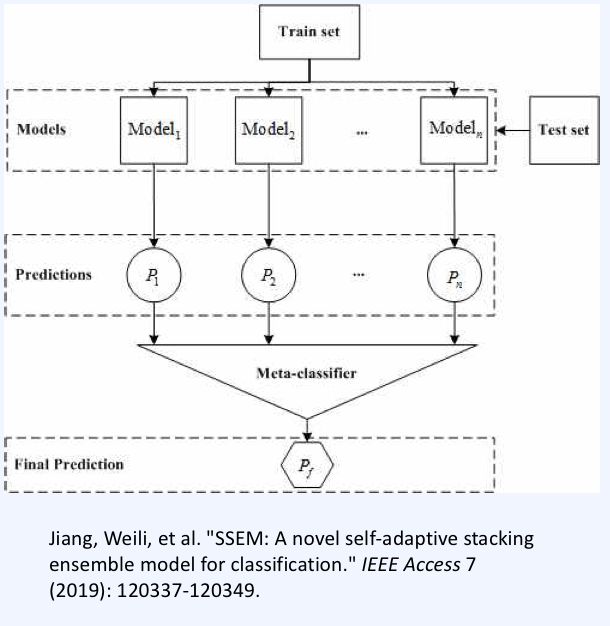
• 각 모델을 병렬적으로 추론하고, 결과를 취합해 다시 학습하는 높은 계층의 Meta-Learning(메타 모델)가 있어, 새로운 결과값을 얻는 방법.

→ 오버피팅이 될 수도 있다.
→ Bias를 줄인다. (Variance 역시 줄일 수 있다.)

4.Dropout

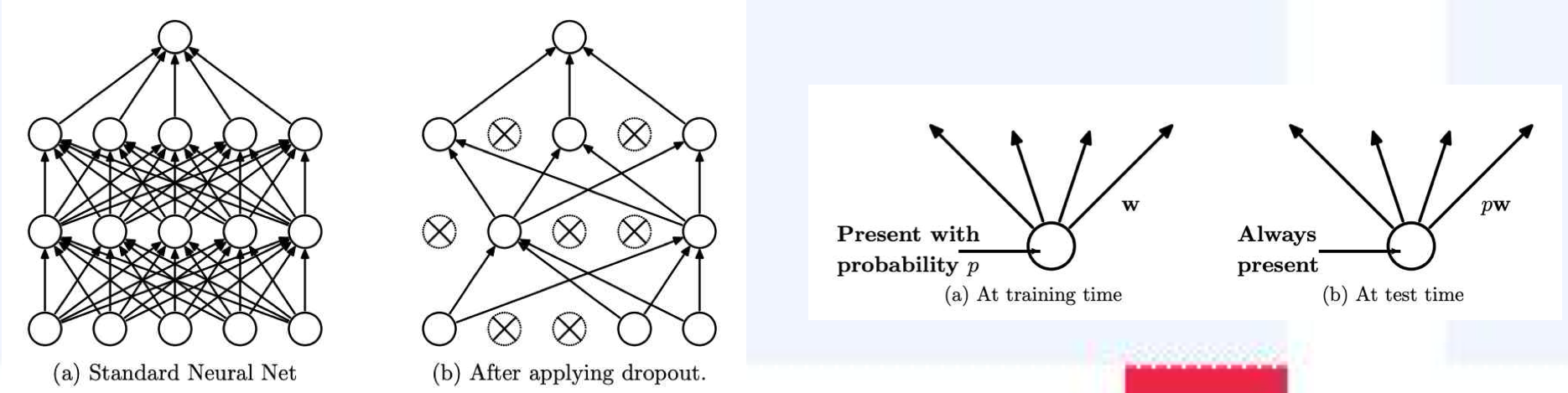
• 학습 시, 임의로 미리 정의된 확률 대로, 뉴런(노드)을 드롭(작동시키지 않음) 시킨다.
  
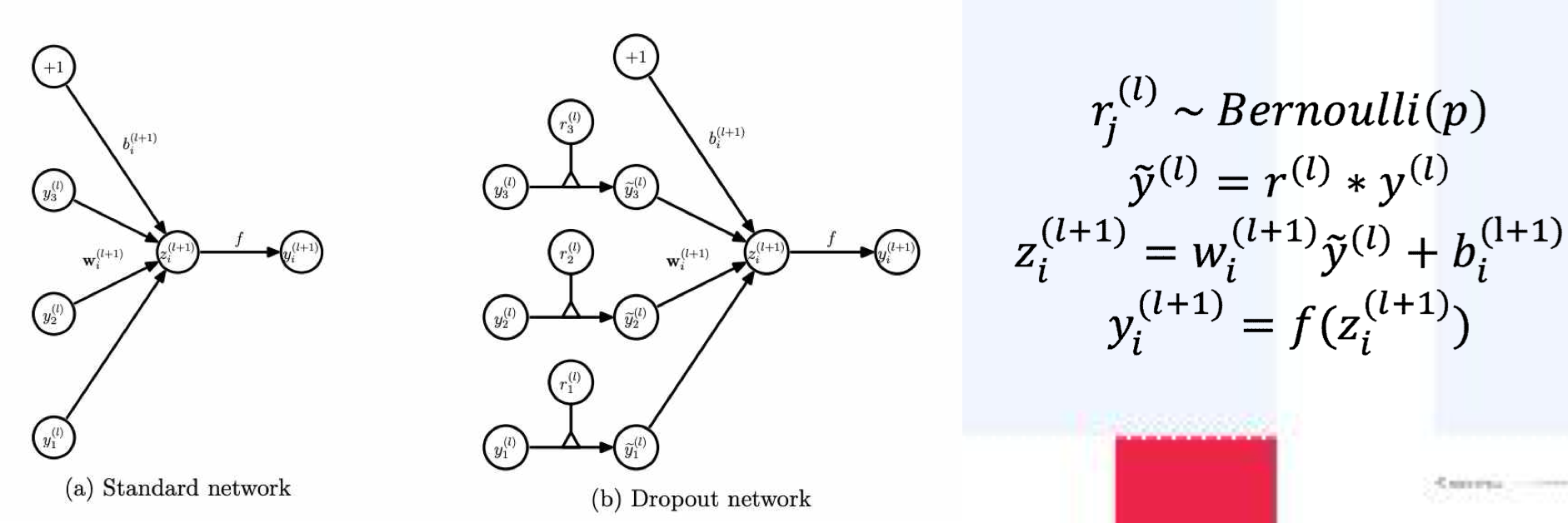
• 각각의 layer는 베르누이 확률 분포(Bernoulli distribution)을 따르는 확률 변수 $r$에 따라, 그 뉴런의 결과 값을 덮어 씌운다. (키거나 끈다.)

Dropout이 잘 되는 이유는 무엇일까?
(심플하면서 powerful)

• 드롭아웃이 뉴런들을 지우고 학습함에 따라, 결과적으로 'weight'를 공유하는 수많은 네트워크의 조합이 생긴다.
  → n개의 뉴런으로 이루어진 네트워크에서 $2^n$개의 조합이 생긴다.

많은 다른 ANN을 한번의 학습으로부터 Bagging하는 효과와 비슷!
→ overfitting을 막는 효과

Dropout vs Bagging
1. Bagging을 각 모델이 파라미터를 share하지 않는 반면,
Dropout은 모든 모델이 파라미터를 공유(share)한다.
2. Bagging의 경우 각 모델이 학습됨에 따라 하나의 모델로 수렴하지만, Dropout의 경우, 각각의 모델이 수렴하도록 학습되지 않는다.
3. Bagging은 모델 결과 값의 산술 평균을 취할 수 있는 것에 비해, Dropout은 지수 계수로 증가하는 많은 모델의 평균을 내는 것이기 때문에, 산술 평균으로는 계산이 어려워진다.

→ 빠른 추론을 위해 dropout은 산술 평균보다 기하 평균(geometric)을 추론하여 근사하는 것에 가깝다.

Dropout의 장점

1. Dropout은 다른 정규화 방법보다 성능이 좋은 것으로 알려져 있다.
2. 컴퓨팅 계산이 작다. $O(n)$ (n은 노드의 개수)
3. 다른 regularizer에 비해, dropout은 모델과 학습과정에서의 종류를 제한하지 않는다. → SGD로 학습하는 거의 그대로 학습시키면 된다.

Dropout이 feature에 끼치는 영향
Dropout은 피쳐들끼리 상호 적응(co-adapatation)을 하는 것을 막아준다.
→ 뉴런들은 다른 뉴런이 그 자리에 없더라도 정상 작동하여야 한다.

Dropout은 결과적으로, 네트워크에 sparse한 활성화를 시켜준다!

5. Early-Stopping

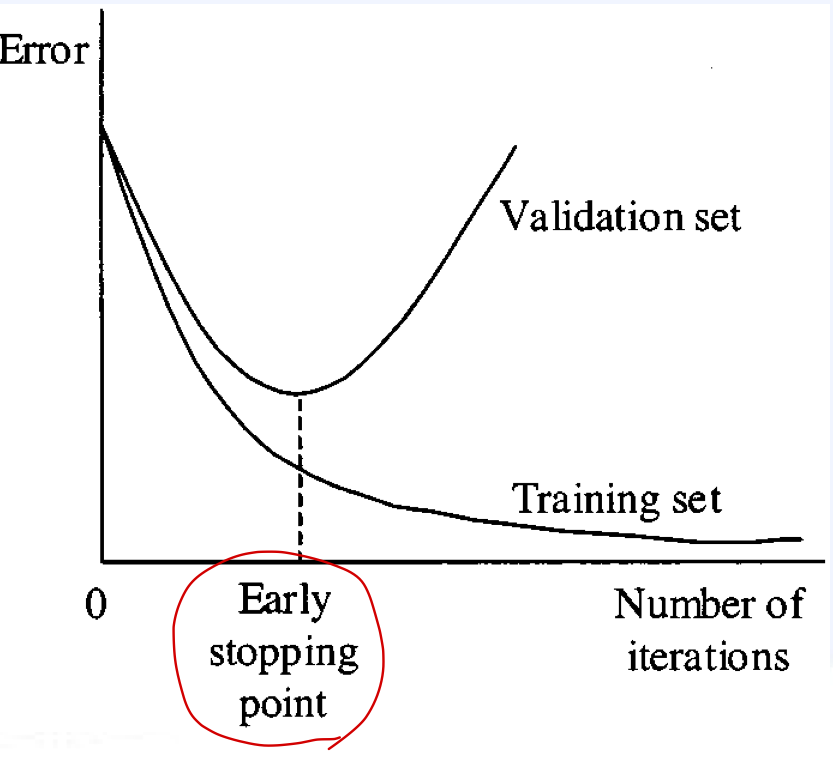
큰 모델을 학습할 때, Train error는 학습이 진행되면서 점점 내려가지만, Validation error는 감소하다가 어느 순간부터 다시 증가한다.
→ 이때 멈춘다면, 최적의 결과를 얻는다는 개념이 Early Stopping

6. 적대적 학습(adversarial training)

사람이 관측할 수 없을 정도의 작은 노이즈를 넣으면, 완전 다른 클래스가 나올 수 있다.
입력은 아주 조금 바뀌었으나, 출력이 매우 달라지며, 그때의 기울기가 매우 가파르다.
→ 일종의 오버피팅 상태.
→ 이런 현상을 생각해 노이즈를 섞어 학습을 진행한 것.
우리가 각 인풋을 노이즈를 섞어 $\sigma$ 만큼 바꿀 때, $\sigma||w||_1$ 변화 한다고 할 수 있다. 이 때, $w$가 만약 높은 차원이라면 그 값은 매우 커질 수 있는 것.

적대적 학습은 로컬 상수 값(노이즈)을 추가한 데이터를 학습하여, 이러한 "locally linear behavior"로 인해 생기는 네트워크의 민감성(sensitivity)을 줄일 수 있다.

7. 데이터 증강(Data augmentation)

ML모델이 가장 일반화하는 쉬운 방법은 "더 많은 데이터"가 학습되는 것이다.
→ 수많은 데이터 증강법이 존재하고 성능이 좋다진다는 것이 널리 알려져 있음.

• 색을 다르게 하기
• 여러 개의 이미지를 단순히 섞는 것(sample paring)
• Random Erasing (CutOut regularization)
• MixUp
  • 일반 ERM은 두 클래스간의 decision boundary가 매우 뚜렷하여 정확하게 분리된다.
    → 오버피팅의 위험성
  • MixUp은 두 클래스 간의 decision boundary가 ERM에 비해서 부드럽다.
    → MixUp이 ERM에 비해서 과적합이 덜 발생한다는 것.
• 모델 같이 이용하기