문제 링크

파이프 옮기기 1

문제 설명

N*N크기의 격자판 (1,1),(1,2)에 걸쳐서 파이프가 놓여있다. 파이프를 (N,N)칸까지 미뤄서 옮기려고 하는데, →, ↘, ↓의 세 방향으로만 밀 수 있다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
아래의 사진은 파이프가 놓인 방향에 따라 밀 수 있는 경우의 수를 나타낸다.



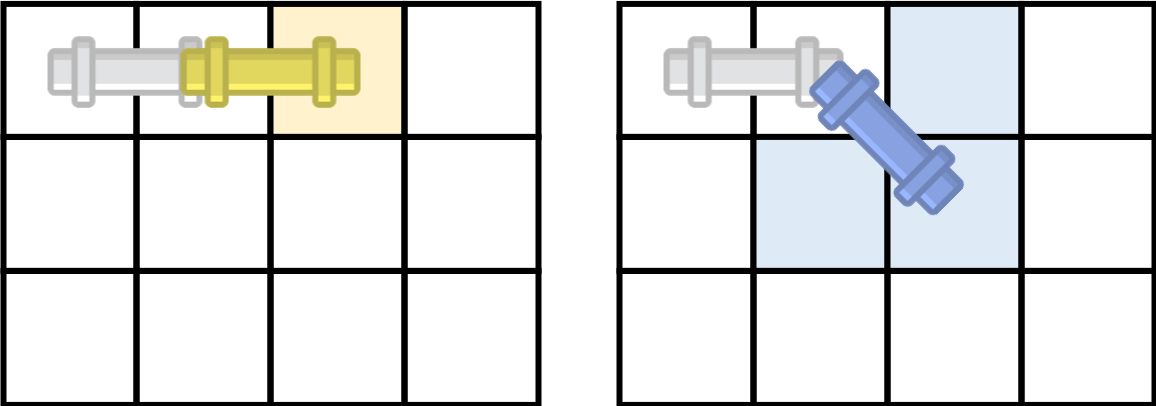
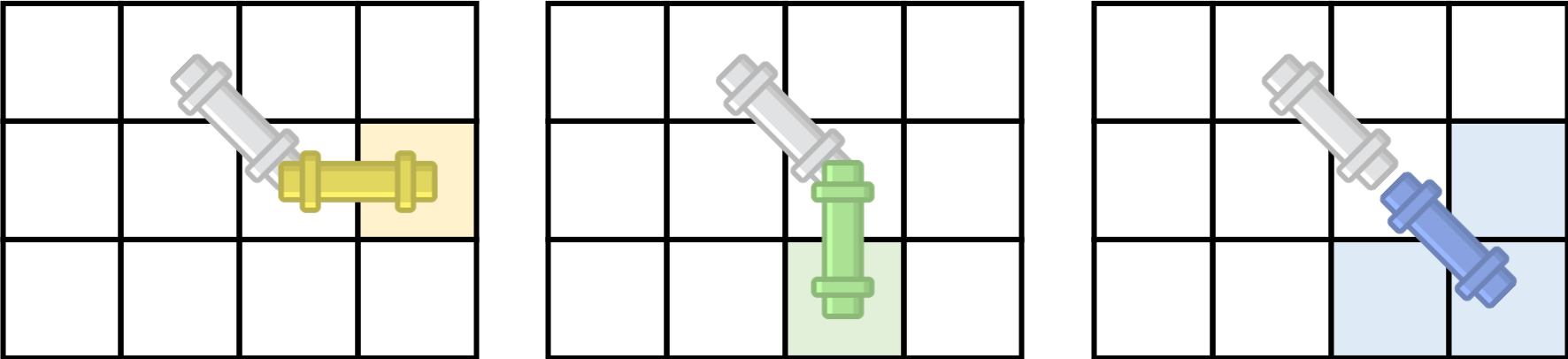
벽을 피해서 파이프를 N*N까지 밀 수 있는 경우의 수를 구하라 .

문제 풀이

구글링하다가 안건데, 파이프 옮기기 문제는 같은 문제 다른 조건으로 두 문제가 있다. 파이프 옮기기 1은 N(3 ≤ N ≤ 16)에 1초, 파이프 옮기기 2는 N(3 ≤ N ≤ 32)에 0.5초,,,,
파이프 옮기기 1은 dfs로, 파이프 옮기기 2는 dp로 풀기를 의도하고 만든 문제인것 같은데 python을 이용해서 dfs로 1을 풀면 시간초과가 나서 둘다 dp로 풀었다 ^_ㅠ

시도 1 - dfs

dfs를 돌면서, 현재 방향에서 이동할 수 있는 모든 경우에서 재귀를 돌았다. 89%에서 시간초과 ^_ㅠ

import sys

input = sys.stdin.readline

N = int(input())
board = []
for _ in range(N):
    board.append(list(map(int, input().split())))
pipe = [0,1]
pipe_dir = 0 #0:가로, 1:세로, 2:대각선
answer = 0

def in_range(x, y):
    if x in range (N) and y in range(N):
        return True
    return False

def dfs(x, y, pipe_dir):
    global answer
    if x == N-1 and y == N-1:
        answer += 1
        return
    #가로인 경우
    if pipe_dir == 0 or pipe_dir == 2:
        if in_range(x, y+1) and board[x][y+1] == 0:
            dfs(x, y+1, 0)
    if pipe_dir == 1 or pipe_dir == 2:
        if in_range(x+1, y) and board[x+1][y] == 0:
            dfs(x+1, y, 1)
    if in_range(x+1, y+1) and board[x][y+1] == board[x+1][y] == board[x+1][y+1] == 0:
        dfs(x+1, y+1, 2)

dfs(pipe[0], pipe[1], pipe_dir)
print(answer)

시도 2 - dp

dp 배열을 방향까지 포함한 3차원 배열로 만들어서 풀이한다.

상태 정의

$d[x][y][dir]$ : dir방향으로 (x,y)까지 도달할 수 있는 경우의 수
가로 : $d[x][y][0] = d[x][y-1][0] + d[x][y-1][2]$
세로 : $d[x][y][1] = d[x-1][y][1] + d[x-1][y][2]$
대각선 : $d[x][y][2] = d[x-1][y-1][0] + d[x-1][y-1][1] + d[x-1][y-1][2]$

초기 상태인 dp[0][1][0]의 경우의 수를 1로 초기화해주고, 이동할 수 있는 범위 (0,2) 부터 포문을 돌면서 각각의 방향에 대해 계산해준다. 파이프가 두칸을 차지하지만 (0,1)에서 (N-1,N-1)까지 도달하면 되므로 한칸만 고려해줘도 된다.

import sys

input = sys.stdin.readline

N = int(input())
board = []
for _ in range(N):
    board.append(list(map(int, input().split())))
pipe = [0,1]
pipe_dir = 0 #0:가로, 1:세로, 2:대각선
dp = [[[0]*3 for _ in range(N)] for _ in range(N)]
dp[0][0][0] = 1
dp[0][1][0] = 1

for x in range(N):
    for y in range(2, N):
        #대각선으로 이동
        if board[x][y-1] == board[x-1][y] == board[x][y] == 0:
            dp[x][y][2] = dp[x-1][y-1][0] + dp[x-1][y-1][1] + dp[x-1][y-1][2]
        
        if board[x][y] == 0:
            #가로로 이동
            dp[x][y][0] = dp[x][y-1][0] + dp[x][y-1][2]
            #세로로 이동
            dp[x][y][1] = dp[x-1][y][1] + dp[x-1][y][2]

print(dp[N-1][N-1][0] + dp[N-1][N-1][1] + dp[N-1][N-1][2])