문제 링크

LCS

문제 설명

LCS는 수열 A와 수열 B가 주어졌을때 두 수열의 공통된 부분 수열중 제일 긴 것을 의미한다.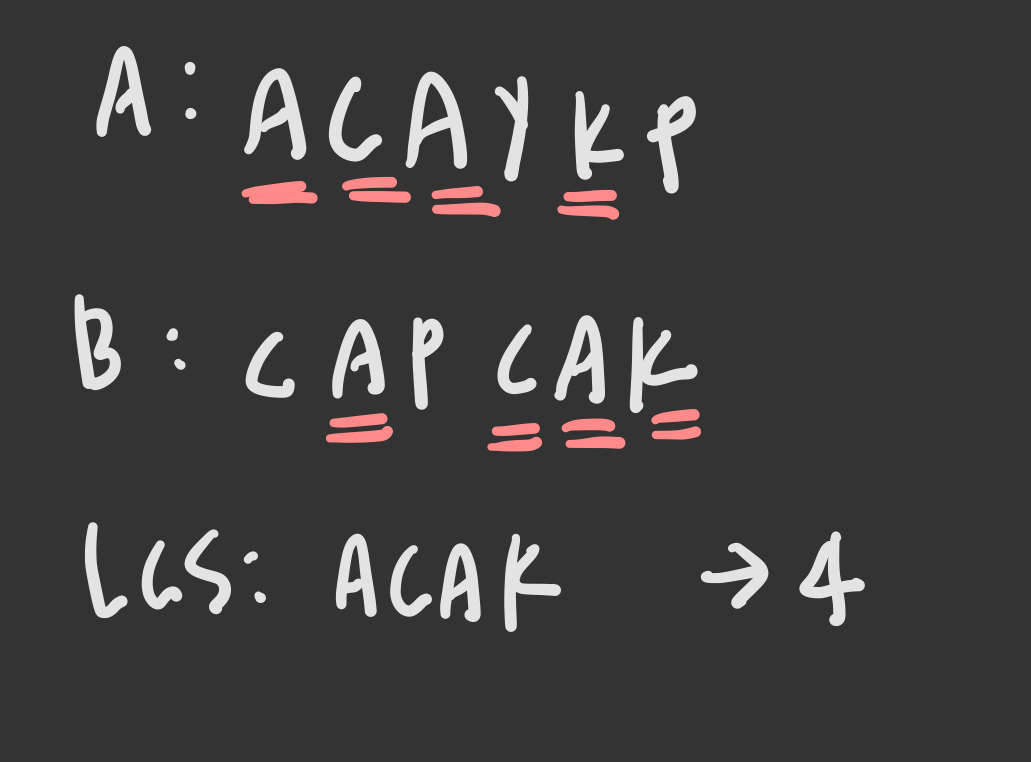
예를 들어 두 수열 ACAYKP와 CAPCAK의 경우, LCS는 위와 같이 ACAK가 된다.
두 수열이 주어졌을때, LCS의 길이는?

문제 풀이

어제 풀었던 편집거리 문제와 같은 방식으로 접근하면 된다.

1. 상태 정의하기
   $L[i][j] : str[:i]과 str2[:j]의 LCS 길이$
   $L[i][j]= \begin{cases} L[i-1][j-1] + 1, &\text{if } str1[i-1] == str2[j-1]\\ max(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]), &\text{else } \end{cases}$
   다른 경우의 점화식은 아래 그림의 경우로 이해하면 빠르다. 근데 지금보니까 굳이 dp[i-1][j-1]의 비교는 하지 않아도 될 것 같은데,,
   
2. 코드

import sys

input = sys.stdin.readline

str1 = input().strip()
str2 = input().strip()
n, m = len(str1), len(str2)

dp = [[0]*(m+1) for _ in range(n+1)]

for i in range(1, n+1):
    for j in range(1, m+1):
        if str1[i-1] == str2[j-1]:
            dp[i][j] = dp[i-1][j-1] + 1
        else:
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-1], dp[i][j-1])

print(dp[n][m])

느낀점

문자열의 dp를 보고 바로 저 방법을 떠올리기 쉽지 않은 것 같다,, 여러개 풀어봐야지 뭐,, dp 정복 그날까지~