문제 설명

N*M크기의 금광이 1*1크기의 칸으로 나누어져 있고, 각 칸은 특정 크기의 금이 있다. 채굴차가 첫번째 열에서 출발하여 금을 채굴하는데, 이동은 오른쪽 위, 오른쪽, 오른쪽 아래 3가지만 가능하다. 채굴자가 m번의 이동을 했을때 얻을 수 있는 최대 금의 크기는 ?

문제 풀이

완탐으로 풀어도 되지만, x축의 이동방향이 항상 오른쪽이므로 특정 칸 board[x][y]에서의 최대값은 이전 칸의 최대값 + 현재 칸의 금 크기이므로 dp를 사용해서 푼다.

1. 상태 정의하기

• board[x][y] : (x,y)칸의 금의 크기

• $G_{x,y}$: 1열부터 (x,y)칸까지 채굴할 수 있는 최대 금의 크기
  라고 했을때,
  
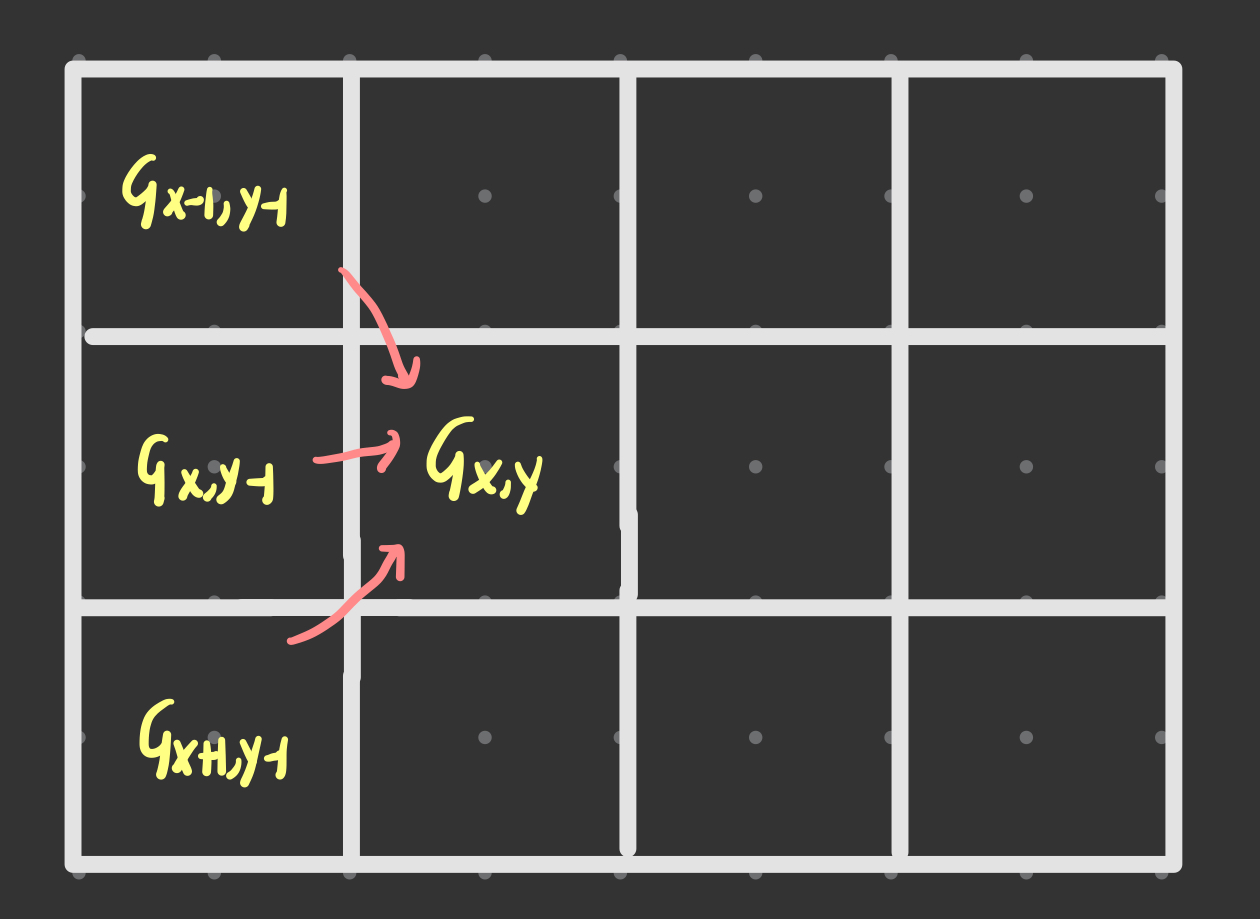
  $G_{x,y}$는 $G_{x,y}$를 도달할 수 있는 세 칸중 가장 큰 값 + 현재 칸의 금 크기이다.

  $G_{x,y} = board[x][y] + max(G_{x+1,y-1}, G_{x,y-1}, G_{x-1,y-1})$
  

2. 코드

import sys

input = sys.stdin.readline

def in_range(x,y):
    if x in range(n) and y in range(m):
        return True
    return False

def get_max_gold(n, m, gold):
    result = 0

    #m회 이동만큼
    for j in range(1, m):
        # i번째 열의 행 확인하기
        for i in range(n):
            #세 방향의 범위 확인하기
            #왼쪽위
            if in_range(i+1, j-1):
                left_up = gold[i+1][j-1]
            else:
                left_up = 0
            #왼쪽
            left = gold[i][j-1]
            #왼쪽아래
            if in_range(i-1, j-1):
                left_down = gold[i-1][j-1]
            else:
                left_down = 0
            gold[i][j] += max(left_up, left, left_down)
    for i in range(n):
        result = max(result, gold[i][m-1])
    return result

tc = int(input())
answer = []

for i in range(tc):
    n, m = map(int, input().split())
    tmp = list(map(int, input().split()))
    
    gold = []
    idx = 0
    for j in range(n):
        gold.append(tmp[idx:idx+m])
        idx += m
    answer.append(get_max_gold(n, m, gold))
print(answer)

점화식은 금방 생각해냈는데 구현하는게 어려웠다 ㅠㅠ.. dp 정복 그날까지 ,,