신장 트리
하나의 그래프가 있을때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
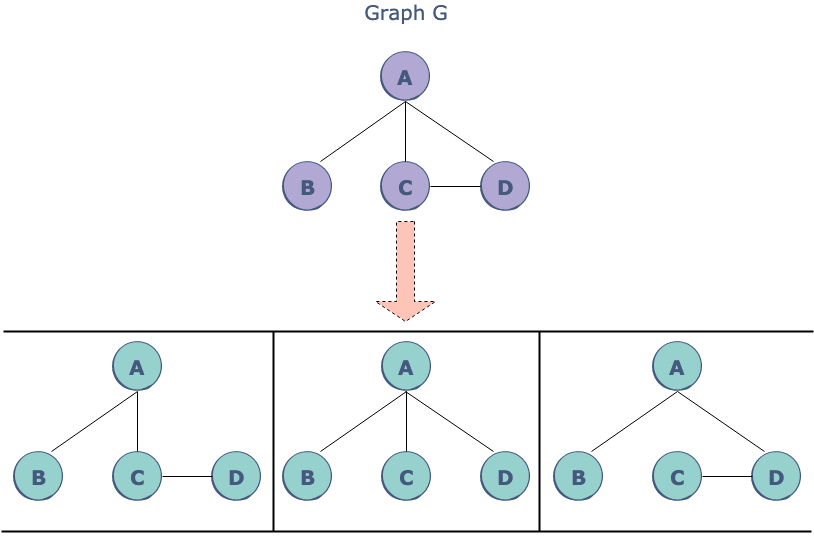
그래프 G에서 나올 수 있는 신장트리는 위와 같다.
크루스칼 알고리즘
크루스칼은 대표적인 최소 신장트리를 찾는 알고리즘이다.
예를 들어 다음과 같은 문제가 최소 신장트리를 찾는 문제이다.
N개의 도시가 있는 나라에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있도록 도로를 설치한다. 임의의 두 도시 A,B를 선택했을때 항상 A,B사이에 도로가 존재하도록 도로를 설치하는 하려고 한다. 최소 비용으로 모든 도시를 연결할 수 있는 방법은?
크루스칼 알고리즘은 그리디 알고리즘을 활용한 그래프 알고리즘이다.
동작 방법
- 간선 데이터를 비용에 따라 오름차순 정렬
- 가장 거리가 짧은 간선부터 하나씩 사이클을 발생시키는지 확인
-> 간선을 이루는 두 노드가 같은 집합에 포함되는지?
2.1 사이클이 발생하지 않는 경우 최소 신장 트리에 포함
-> union 연산 사용
2.2 사이클이 발생하는 경우 최소 신장 트리에 포함 x - 모든 간선에 대해 2 반복
완성된 최소 신장 트리의 간선의 비용을 모두 더하면 최소비용을 알 수 있다.
소스코드
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화하기
# 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# 모든 간선에 대한 정보를 입력 받기
for _ in range(e):
a, b, cost = map(int, input().split())
# 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
print(result)출처
나동빈님의 이것이 취업을 위한 코딩테스트다 with python 의 Chapter 10. 그래프 이론
https://www.educative.io/edpresso/what-is-a-spanning-tree
