나동빈님의 코딩 테스트를 위한 벨만 포드 알고리즘 7분 핵심 요약을 보고 공부한 내용입니다.
벨먼-포드 최단경로 알고리즘
: 음수 간선이 포함된 경우에서 한 노드에서 다른 노드로 가는 각각의 최단경로 구하기
특징
- 가중치가 음수여도 계산 가능
<-> 다익스트라의 가중치는 양수여야함 - 음수 간선의 순환 또한 감지 가능
- 시간복잡도 : → V는 노드의 개수, E는 간선의 개수
음수 간선의 최단 경로
- 모든 간선이 양수인 경우
- 음수 간선이 있는 경우
2.1 음수 간선의 순환이 없는 경우
2.2 음수 간선의 순환이 있는 경우
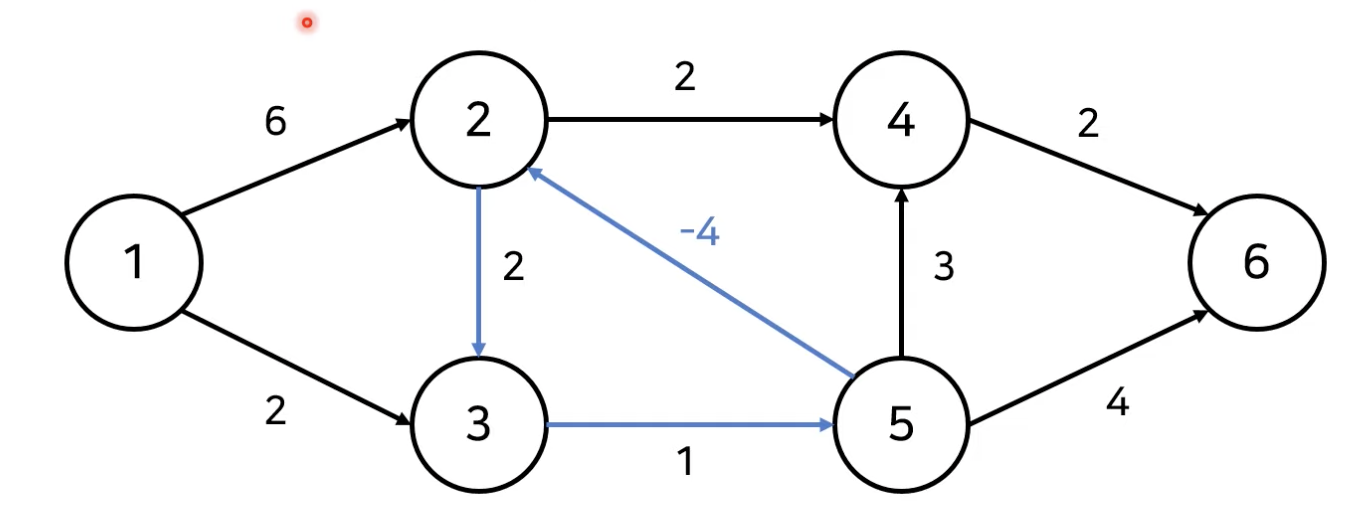
2->3, 2->5 등의 경우
-> 최단 거리가 음의 무한이 될 수 있음
동작 원리
- 출발 노드 설정, 최단 거리 테이블 무한으로 초기화
- N-1번 아래 과정 반복
2.1 전체 간선 E개 확인
2.2 각 간선을 거쳐 다른 노드로 가는 비용 계산 -> 최단 거리 테이블 갱신 - N번째 반복했을때 최단 거리 테이블이 갱신되면 음수 간선의 순환 존재
구현
import sys
input = sys.stdin.readline
INF = int(1e9)
def bf(start):
#시작 노드에 대해서 초기화
dist[start] = 0
#전체 N번의 라운드 반복
for i in range(n):
#모든 간선 확인하기
for j in range(m):
now = edges[j][0]
next_node = edges[j][1]
cost = edges[j][2]
#현재 간선을 거쳐서 다른 노드로 이동하는게 더 짧은 경우
if dist[now] != INF and dist[next_node] > dist[now]+cost:
dist[next_node] = dist[now]+cost
if i == n-1:
return True
return False
n, m = map(int, input().split())
edges = []
dist = [INF]*(n+1)
for _ in range(m):
a, b, c = map(int, input().split())
edges.append((a,b,c))
if bf(1):
#음수 간선의 순환이 존재하는 경우
print("-1")
else:
for i in range(2, n+1):
if dist[i] == INF:
#도달할 수 없는 경우
print("-1")
else:
#도달할 수 있는 경우
print(dist[i])
다익스트라 vs 벨만포드
다익스트라
- greedy의 활용 : 매번 방문하지 않은 노드 중 비용이 제일 적은 것 선택
- 음수 간선은 포함 x
벨만 포드
- 모든 간선 확인
-> 다익스트라의 최적해 항상 포함
-> 다익스트라보다 더 오래걸림 - 음수 간선 포함해도 계산 가능
