[논문리뷰] Revising Densification in Gaussian Splatting

0. 리뷰하는 이유

• 3DGS의 ADC (Adaptive Density Control)가 아름 답지 못하다는 생각을 해왔음
• End-to-End manner가 아니라 Heuristic한 측면이 크다는 점이 마음에 안들었음.
• scene에 따라 최적인 hyper-parameter(iteration)가 다를 수 있다는 것이 마음에 안들었음.
• 이것 또한 미분 가능한 연산자로 대체해서 자연스럽게 동작하면 어떨까? 하는 생각이 있었음
• ADC의 문제와 해결방법을 비교적 잘 제시하고 있는 논문을 발견해서 인사이트 얻고자 리뷰

1. Contributions (병주 요약)

• 3DGS의 ADC logic의 한계를 지적하였음. 이에따라 3가지 solution제안

1. pixel-error driven density control을 제안
2. cloning 직후 opacity correction
3. gaussian의 total number를 control하는 방법 제안

• 적절한 densification logic 수정으로 qual, quan에서 개선을 가져옴.

2. Details and Limitation of ADC

• general notation
  

• ADC는 densficiation iteration(=100)마다 positional gradient magnitude $\tau_k$와 opacity $\alpha_k$를 기준으로 동작한다
  

• 직관적으로, $\tau_k$가 크다는 의미는 $\mu_k$의 변동이 크다는 의미기에, 현재 stable된 영역 보다는 열심히 fitting중인 영역이라고 볼 수 있다.
  

2.1. Growing

• densification 주기가 찾아오면, $\tau_k$가 특정 threshold를 넘는 $\gamma_k$는 split 또는 clone이라는 과정으로 grow할 수 있다.
• $\Sigma_k$의 largest eigenvalue로 동작이 결정된다; 또 다른 threshold를 넘으면 split되고, 넘지 않으면 clone된다. ($\gamma_k$의 크기가 큰지 작은지 판단함)
• split: 하나의 $\gamma_k$를 두 개로 분리하는 과정.
  1. $\mu$ $\leftarrow$ $\mathcal{G}_k$ 로부터 2개를 sample해서 얻음
  2. $\Sigma$ $\leftarrow$ $\Sigma_k$의 scaled-down version으로 얻음
  3. $f$, $\alpha$ $\leftarrow$ $f_k$, $\alpha_k$값 그대로 사용
  
• clone: $\gamma_k$의 모든 값을 그대로 복제

2.2 Pruning

• densification 주기가 찾아오면, $\alpha_k$가 특정 threshold(=0.005) 이하일시, 삭제
• 사용되지 않는 primitive를 삭제하기 위해서, ADC는 큰 주기(3000 iter)로 한 번씩 $\alpha_k$를 0.01로 세팅함.

2.3. Limitations

1. gradient magnitude에 직관적인 threshold 값을 결정하기가 어려움. => 0.1?
2. 적절한 threshold는 model, loss, hyperparameter 변화에 굉장히 sensitive함
3. $\tau_k$가 threshold 아래임에도 불구하고 실제론 underfitting된 경우가 존재함.
   (grass영역에 대해 3DGS는 적은 수의 큰 gaussian들로 표현해서 blurry함. underfitting임에도 불구하고 densification이 제대로 trigger되지 않은 것임)
   
4. 가우시안의 개수를 직접 컨트롤하는 것이 불가능함; 비정상적인 성장이 있을때 OOM문제를 야기할 수도 있음

3. Error-based Densification

• grass의 실패 원인 분석; 이미 grass영역을 크기가 큰 적은 수의 gaussian으로 커버했다고 가정하자. 가우시안에 수집된 전체 positional gradient의 합은 0에 수렴하게 된다.
• 하지만, 그러한 영역은 total error자체는 굉장히 크다. 즉, rendering 결과와 GT사이의 per-pixel error (Structural Similarity)의 크기로 densification을 결정할 수 있다.
• 해결할 문제; 각 가우시안별로 error값을 re-distribution해야 함. prediction 자체가 여러 가우시안의 합으로 만들어진 픽셀들이기에, error에 각자가 얼마나 기여했는지를 계산해야함.
• 픽셀 $\mathbf{u}$에 대해서 per-pixel error를 $\mathcal{E}_\pi(\mathbf{u})$ 라고 정의하자. 그리고 각 $\gamma_k$가 카메라 $\pi$에 대해서 rendering된 pixel color에 얼마나 기여했는지 비율을 $w_k^\pi(\mathbf{u})$라고 하자. 그러면, 모든 픽셀을 돌면서, 다음처럼 계산 가능
  $E_k^\pi = \sum_{\mathbf{u}\in \text{Pix}}\mathcal{E}_\pi(\mathbf{u})w_k^\pi(\mathbf{u})$
• (왠지는 모르지만) 최종 $E_k$는 모든 카메라 각도 $\Pi$중 max를 취했다.
  $E_k := \max_{\pi \in \Pi} E_k^\pi$
• $\tau_k$ 대신에 $E_k$를 지표로 사용하면 위 케이스를 해결할 뿐만아니라, error metric이 친숙한 텀이기 때문에 threshold를 더 직관적으로 결정할 수 있다.
• 구현을 위해서 $\gamma_k$에 $e_k$라는 scala값을 추가해서 $e_k$만 바꿀 수 있는 auxilary loss로 error를 추정함. (논문 참조)

4. Opacity correction after cloning

• 기존 ADC의 문제중 하나 - gaussian이 split되거나 clone될 때, opacity 값이 그대로 유지 되는 것
  
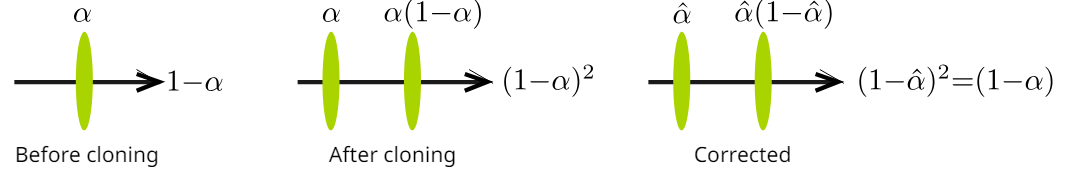
• before clone: rendered color은 다음에 오는 값 * $(1-\alpha)$에 의존됨
• after clone: 다음에 오는 값의 weight가 $(1-\alpha)^2$에 의존됨
• clone이 되든 안되는 뒤에 오는 값의 영향력을 동일한 수준으로 유지해야함; 그렇지 않다면, 새로 clone된 애들한테 더 bias를 주는 행위임
• $\hat{\alpha}:=1-\sqrt{1-\alpha}$로 하면, 다음값의 weight가 $(1-\alpha)$로 유지될 수 있음
• 참고1) $\hat{\alpha}:=1-\sqrt{1-\alpha} = \frac{\alpha_k}{1+\sqrt{1-\alpha_k}}<\alpha_k, \forall \alpha_k \in (0,1)$
• 참고2) $\hat{\alpha}$는 center pixel만 고려한 것으로, bias를 완벽하게 제거할 수는 없다. 그렇지만 모든 픽셀을 고려하더라도 이전보다 bias를 줄인 것임에는 확실하다. 다음 부등식은 항상 성립한다.
  $1-\alpha_k \mathcal{G}_k^\pi(\mathbf{u}) \geq (1-\hat{\alpha}_k \mathcal{G}_k^\pi(\mathbf{u}))^2 \geq (1-\alpha_k \mathcal{G}_k^\pi(\mathbf{u}))^2$
• split에 대해서는 위와 같은 correction을 진행하지 않는다.
  1) 기존 center로부터 random하게 두 위치가 sample되기 때문이며
  2) covariance scale을 낮추기 때문이다.

5. Primitives growth control

• 기존 ADC의 문제중 하나 - densification의 제한이 없고 control이 불가능해서 메모리 예측이나 제어가 불가능함.
• 그냥 사용가능한 budget이상으로 gaussian이 나온다면, highest densification score만 남겨두게 제한을 걸었음
  
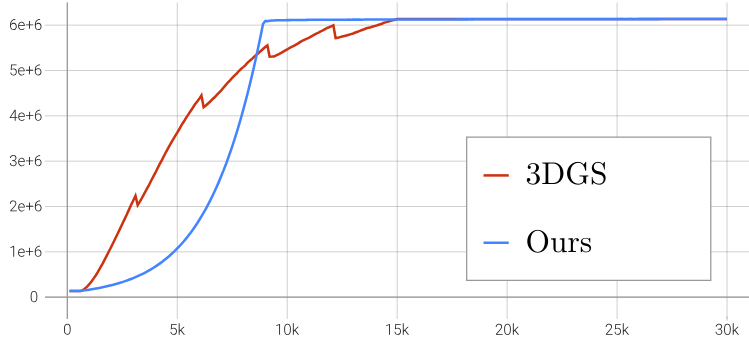
• 그래프에서 3DGS는 3K를 주기로 뾰족점이 생기는 반면 Ours는 smooth하다. 그 이유는 다음 장에서..

6. Alternative to opacity reset

• 기존 ADC의 문제중 하나 - 3k마다 0.01로 모든 $\alpha_k$가 setting이 되는 과정에서, opacity가 더 이상 증가하도록 optimize 되지 않는 gaussian들은 결국 pruning된다. 학습이 stable 하지도 못하다.
• 특히 Error-based densification을 사용시에 임의적인 hard-reset은 error statistics 추정에 크게 악영향을 미친다.
• 대신에, 매 densification이 끝나고나서(100 iter) 0.001씩 opacity를 줄여서, pruning range로 점진적으로 이동하도록 이끈다.
• 이 방법의 단점은, 결국 픽셀에 hole을 만들 수 있다는 점이다.
• 이에 대한 해결 방법 이해를 못하겠음

  To counteract this dynamics, we also regularize the residual probabilities of the alpha-compositing (a.k.a. residual transmittance) to be zero for every pixel, by simply minimizing their average value, weighted by a hyperparameter (here 0.1).

• residual transmittance가 각 픽셀이 최종적으로 얼마나 남아있는지, 얼마나 투명한지를 나타내는 값으로 보이고, 이 값이 0이라는게 투명한 픽셀을 만들지 않겠다는 얘기인거 같음
• 모든 픽셀의 residual probabilties의 평균을 0.1이라는 낮은 값으로 맞춤으로써 0에 가까운 값으로 보내버리려고 함.

7. Result

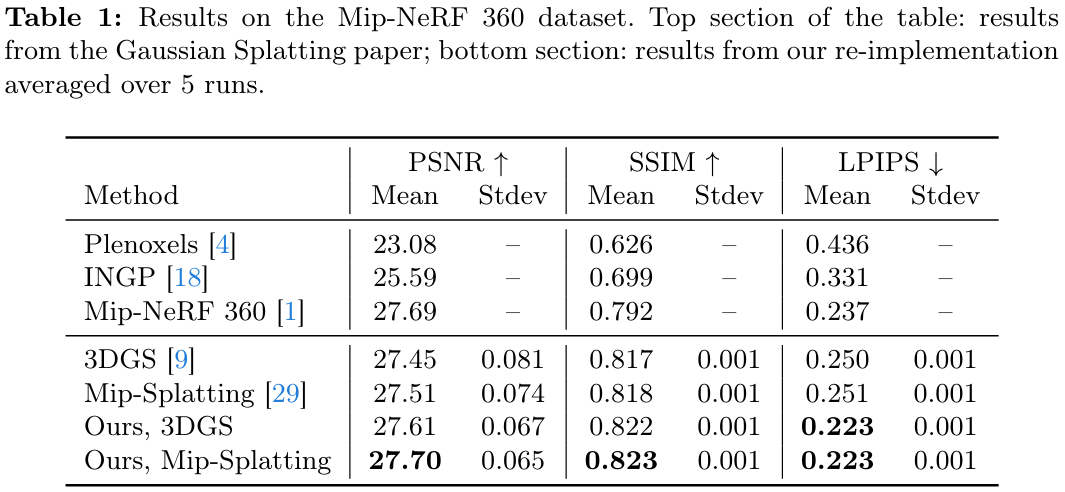
• 3DGS, Mip-Splatting 모두에서 성능을 잘 올렸다
  
• 확실히 high-texture 영역에서 개선이 있다.