[논문리뷰] Modeling uncertainty for Gaussian Splatting

1. Abstract & Introduction

• 일반적으로 3DGS는 output의 confidence 정보를 제공해주지 않는다.
  • epistemic uncertainty
• 이 연구에서는 deterministic GS framework를 stochastic framework로 확장했다. Variational Inference (VI) 방식을 활용해 GS를 Bayesian framework에서 학습하게 하여 uncertainty prediction을 자연스럽게 결합했다.
• 또한 Area Under Sparsification Error (AUSE) 라는 loss를 제안한다
  • reconstruction과정에서 uncertainty estimation을 가능하게 하는 loss
• 실험적으로 LLFF 데이터셋에서 렌더링 퀄리티, uncertainty accuracy 모두 sota
• 생성된 view의 신뢰도는 real-world application에서 안전한 decision making에 도움이 될 것이다.

2. Related work

• 저자는 NeRF에선 Uncertainty를 측정하는 연구가 있지만, GS는 최초라고 주장

Stochastic NeRF: (3DV 2021)

• NeRF의 생성된 view의 epistemic uncertainty estimation을 최초로 다룬논문
• bayesian learning problem으로 보고 variational inferece framework로 품
  
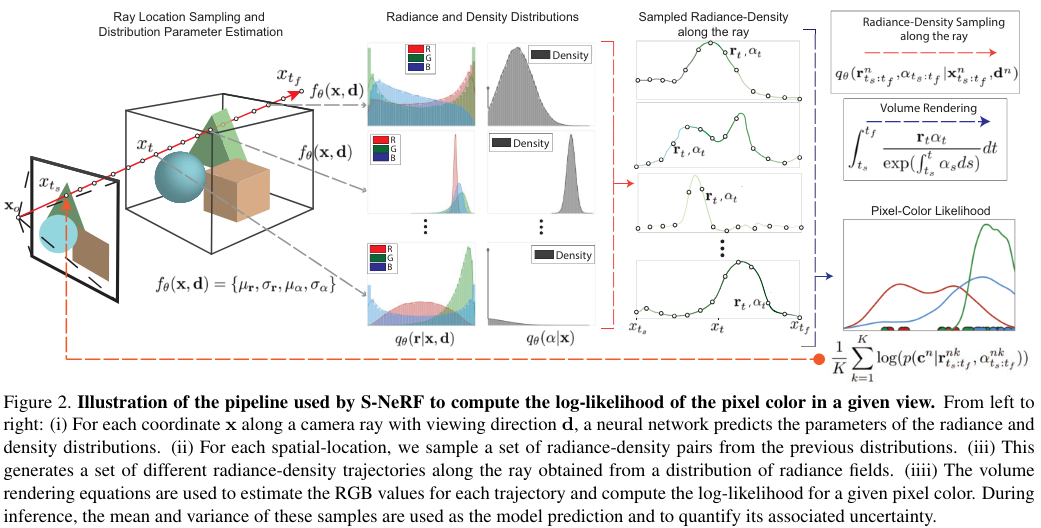
• MLP가 주어진 좌표에 대해서 radiance(=RGB), density 값을 예측하는게 아니고, radiance, density에 대한 distribution의 parameter (mean and variance)를 예측한다.
• 이 distribution에 대해서 radiance-density sampling을 통해서 RGB를 estimate한다 (log-likelihood ?)
• inference시에는, mean을 prediction으로, variance를 uncertainty로 사용한다

CF-NeRF: (ECCV2022, 인용 30)

• stochastic-NeRF와 동일저자의 후속연구: Conditional-Flow NeRF
• color와 opacity의 independence assumptions을 버림 ????
• conditional normalizing flow framework를 사용 ????
• 동일 저자의 "Estimating 3D Uncertainty Field:Quantifying Uncertainty for Neural Radiance Fields" 라는 paper도 있는데 뭐가 다른지 아직 잘모름

3. Important Concepts for Bayesian Framework

Monte Carlo Method

• random sampling을 반복하여 얻은 값들로 함수의 parameter를 추정하는 방식
• 평균을 추정할때 N번 샘플링한 값의 합을 N으로 나누는 것도 Monte Carlo Method임

aleatoric uncertainty

• 데이터 자체의 노이즈로 인한 uncertainty

epistemic uncertainty

• 모델이 데이터를 충분히 설명하지 못함으로 인한 uncertainty; 즉, 모델 parameter의 uncertatinty; 데이터가 많을수록 줄일 수 있음
• bayesian framework로 uncertainty를 모델링 할 수 있음
• monte carlo method로, weight를 샘플링해서 classification의 경우 p의 entropy로, regression은 y의 variance로 uncertainty를 젤 수 있다.
• [이 논문] : (https://papers.nips.cc/paper/2017/file/2650d6089a6d640c5e85b2b88265dc2b-Paper.pdf) 참고: Yarin Gal

Bayesian Framework: 상세한 설명

• given Data $\mathcal{D}$를 잘 모델링(표현)하는 parameter $\theta$를 얻고자 할 때,
  (가령 3DGS의 경우 2d views (image+camera)가 $\mathcal{D}$이며, 이를 3D Gaussian으로 모델링하여 좋은 rendering결과를 내고자 할때, 3DGS의 parameter들의 집합($\mu_k$, $\Sigma_{k}$, $c_{klm}$, $\alpha_k$)을 $\theta$라고 할 수 있다.
  • point estimation: 최적의 $\theta$값을 MLE, MAE같은 방식으로 deterministic하게 결정함.
  • bayesian method: $\theta$ 값이 아니라, $\theta$를 sampling할 수 있는 distribution $p(\theta | \mathcal{D})$을 추정함.
• 그럼 어떻게 $p(\theta | \mathcal{D})$라는 distribution을 모델링할까?
  • variational inference
  • MCMC
  • Ensemble, 등등등
  • dropout: weight를 binomial distribution으로,,

Variational Inference

• VAE의 이해가 VI의 이해에 도움이 된다. VI를 AE로 구현한게 VAE이기 때문: 유튜브, 포스팅
• VI(=변분추론)이란, Posterior Probability Distribution(=사후확률분포)를 단순한 확률분포(e.g., normal) 로 근사하는 것
  • $p(x|z)=q_\phi(x|z)$, $q_\phi$는 normal distribution, $\phi$는 distribution의 parameter
• Hands-on BNN: (650회 인용)이 딥러닝에서 VI framework를 잘 설명한듯

Reparameterization Trick

• VI framework에서, sampling 연산을 미분할 수 없어서 backprop을 사용하지 못하는 문제가 있음
• 키 아이디어: 미분불가능한 stochastic 연산을 deterministic와 stochastic파트로 나누자. ($\mu$와 $\sigma$에만 grad가 흐르면 됨.)
• stochastic한 연산($z$$\sim$$\mathcal{N}(\mu,\sigma)$) -> deterministic한 값 ($\mu$, $\sigma$) & stochastic한 sampling 파트($\epsilon$$\sim$$\mathcal{N}(0,1)$)

• $\epsilon$은 어차피 외부입력으로 gradient가 흐를 필요가 없고, $\mu$와 $\sigma$를 추정하는 network에 gradient흐르는데는 문제 없다!

4. Stochastic Gaussian Splatting

• GS는 color field와 density field를 3d gaussian kernel들로 표현한다. 각각의 gaussian에 대해서 learnable parameter는 4개이다: $\mu_k$, $\Sigma_{k}$, $c_{klm}$, $\alpha_k$
  
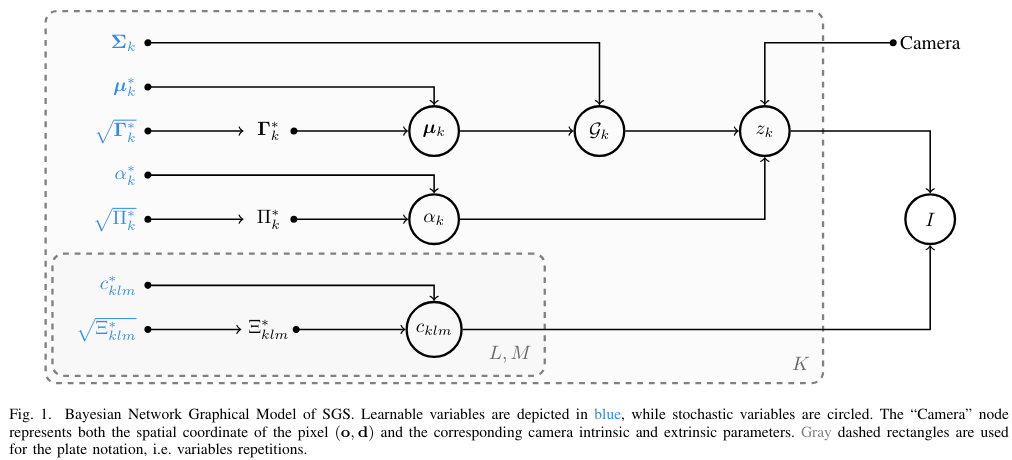
• 이중에서, $\Sigma_{k}$를 제외한 나머지 셋을 random variable로 만들어버리는, Variational Inference Framework를 따랐다. 오리지널 GS param은 이제 distribution에서 sample되는 것이며, 그 distribution parameter들이 새로운 learning variable이다.
  
• reparameterization trick을 이용해서, gradient가 끝까지 전달될 수 있다.

5. AUSE Loss

• AUSE는 Area Under the Sparsification Error의 약어로, 모델이 얼마나 불확실성을 잘 측정했는지를 나타낼 수 있는 하나의 지표이다 (ECE와 좀 다름)
• 과정
  1. Bayesian Model로 prediction을 한다. 그 predicted value를 predicted uncertainty가 높은 순으로 정렬한다.
  2. uncertainty가 높은 샘플을 순서로 조금씩 제거했을때 모델 성능(error 등)이 어떻게 변화는지 plot을 찍는다. (가령, 0% 제거시 성능이 70%인데 5%제거시 성능이 74%로 오르는 등). 이를 Sparsification Curve라고 부른다
  3. 이 모델과 oracle model 사이의 면적값이 AUSE이다. 이 때, oracle 모델은 true error로 가능한 가장 완벽한 제거 순서이다. 즉, true error map과 uncertainty 값을 일치시키는 과정이다.
  

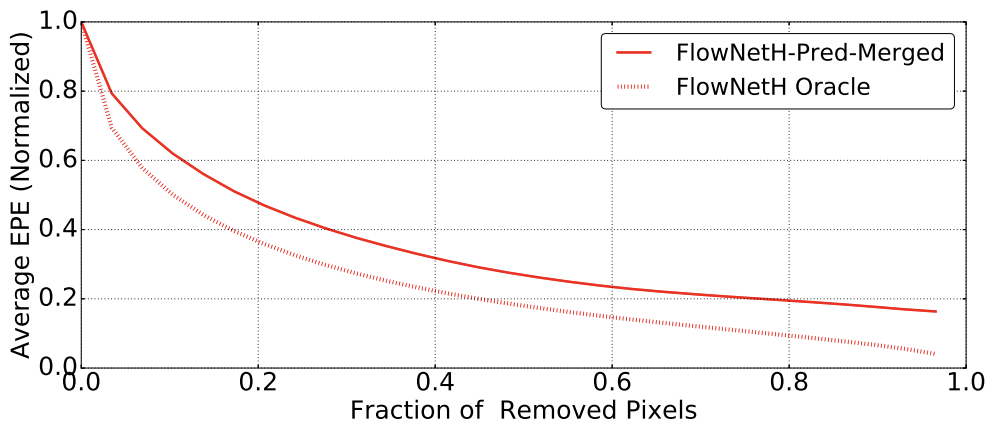
If the estimated variance is a good representation of the model uncertainty, and the pixels with the highest variance are removed gradually, the error should monotonically decrease

• 만약 uncertainty가 random이면, 제거 되는 순서도 random이기에, curve는 flat할 것이다. 따라서 AUSE는 클것이다. 반면, 정말로 uncertainty가 높은 순으로 잘 정렬되었다면, oracle과 일치할 것이다.

---

• 이 연구에서는 std를 uncertainty로써 view에 있는 모든 pixel에 대해서 AUSE를 계산했다. 이는 GS의 rendering속도가 굉장히 빠르기에 가능하다.
• 이 값의 RMSE 또한 loss로 썻다

6. Overall

• 이 loss로 학습을 시켰다.
• KL loss는 BNN을 수식전개하면 원래 생기는 텀으로, 우리가 parameter의 분포를 우리 맘대로 가우시안이라고 박았으니, 원래 파라미터의 분포를 가우시안이 나오도록 일치시키는 loss라고 볼 수 있다.
  

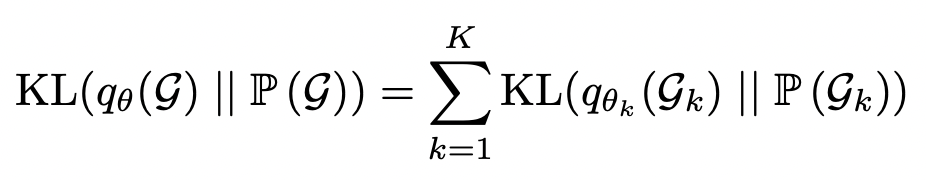
• distribution에 prior를 주었다. KL loss 같은 경우는 Gaussian의 center을 fix하는 경향이 있어, convergence에 어려움을 야기한다고 한다. 따라서 center에 대한 impormative prior를 주기 위해서, classic GS로 iteration을 돌린 후 그 값을 SGS의 initialization으로 쓴다고 한다.
  
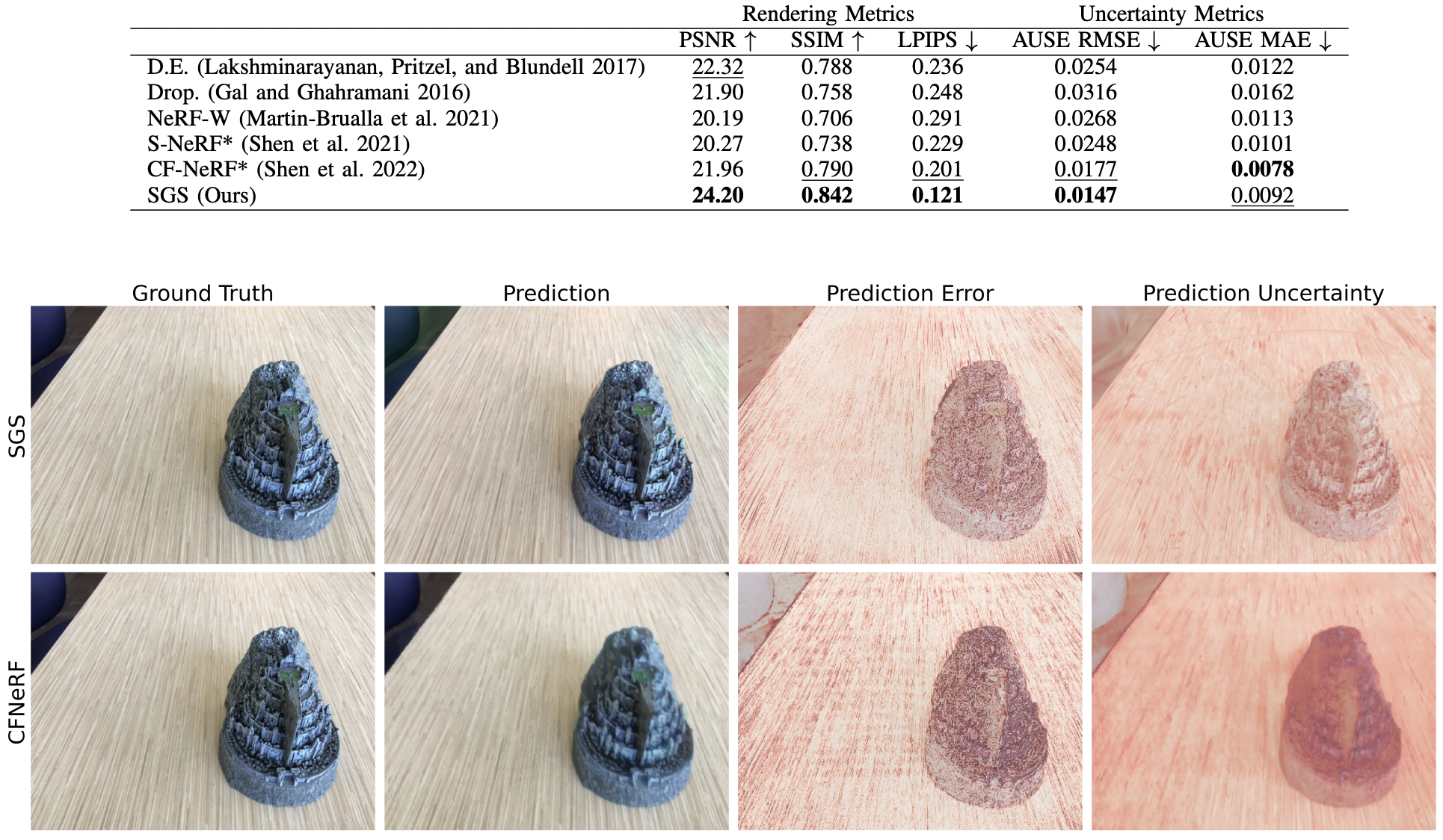
• 중요한점은, AUSE loss ablation해보니 이 로스를 빼야 성능이 올라간다는 것이다. 즉, uncertainty를 잘 측정할 수록 모델 성능이 낮아지는 trade-off가 있다고 하였다.