Python의 List Comprehension
- 파이썬은 리스트를 선어할 때 직관적이고 짧은 코드를 가지고 만들수 있도록 해주는 기능인 List Comprehension 이라는 강력한 기능을 지원한다.
- 처음보면 생소해서 어렵게 느낄 수 있지만 사용하다보면 금방 익숙해진다.
리스트 컴프리헨션을 사용하지 않고 선언
squared_numbers = []
for x in range(10):
squared_numbers.append(x**2)
리스트 컴프리헨션을 사용한 선언
squared_numbers = [x**2 for x in range(10)]List Comprehension 을 사용하면 위와 같이 상대적으로 코드가 직관적이고 간결해진다.
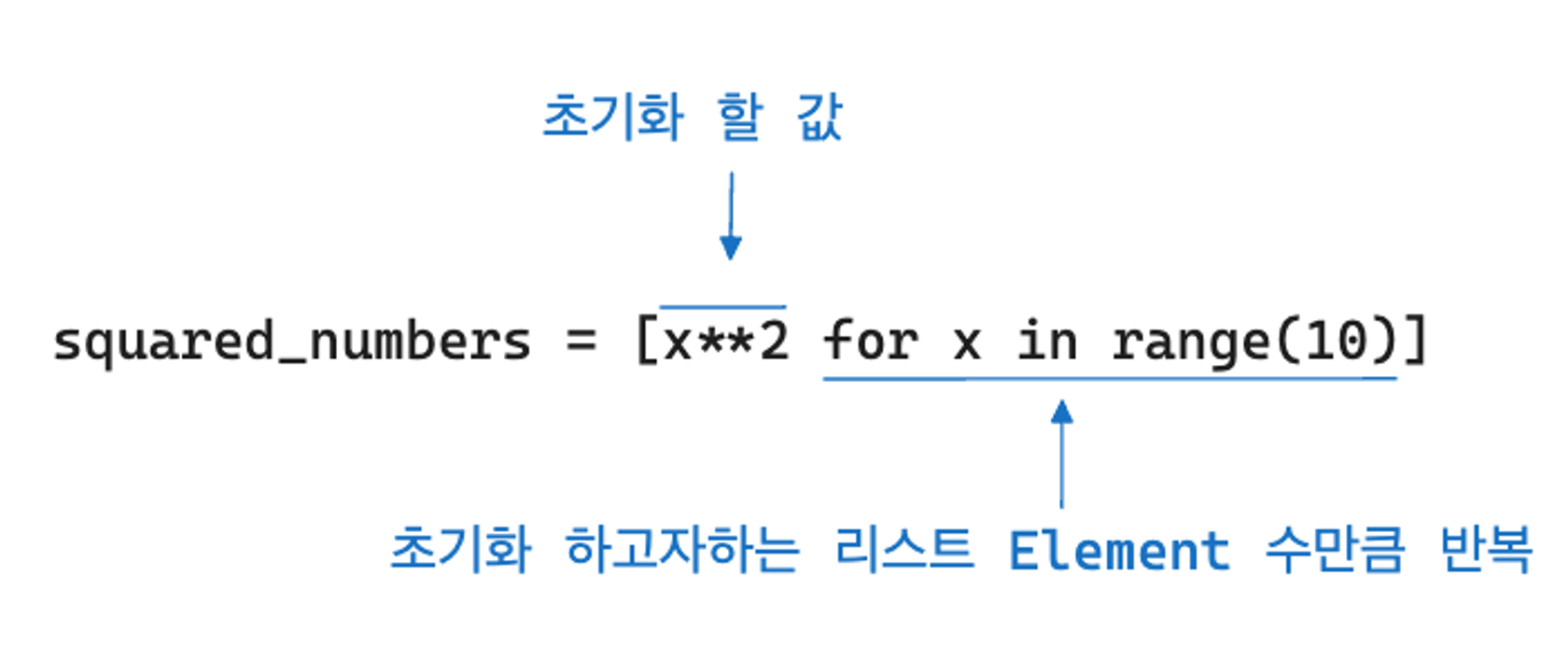
리스트 컴프리헨션으로 초기화 하는 과정은 간단하게 생각하면 초기화할 값 + 반복문으로 구성된다고 보면된다.
이제 리스트 컴프리헨션을 사용하여 그래프 구현에 자주 사용되는 자료구조들을 선언해보자.
인접 리스트 선언
- 빈 리스트 N개를 원소로 하는 리스트를 선언한다.
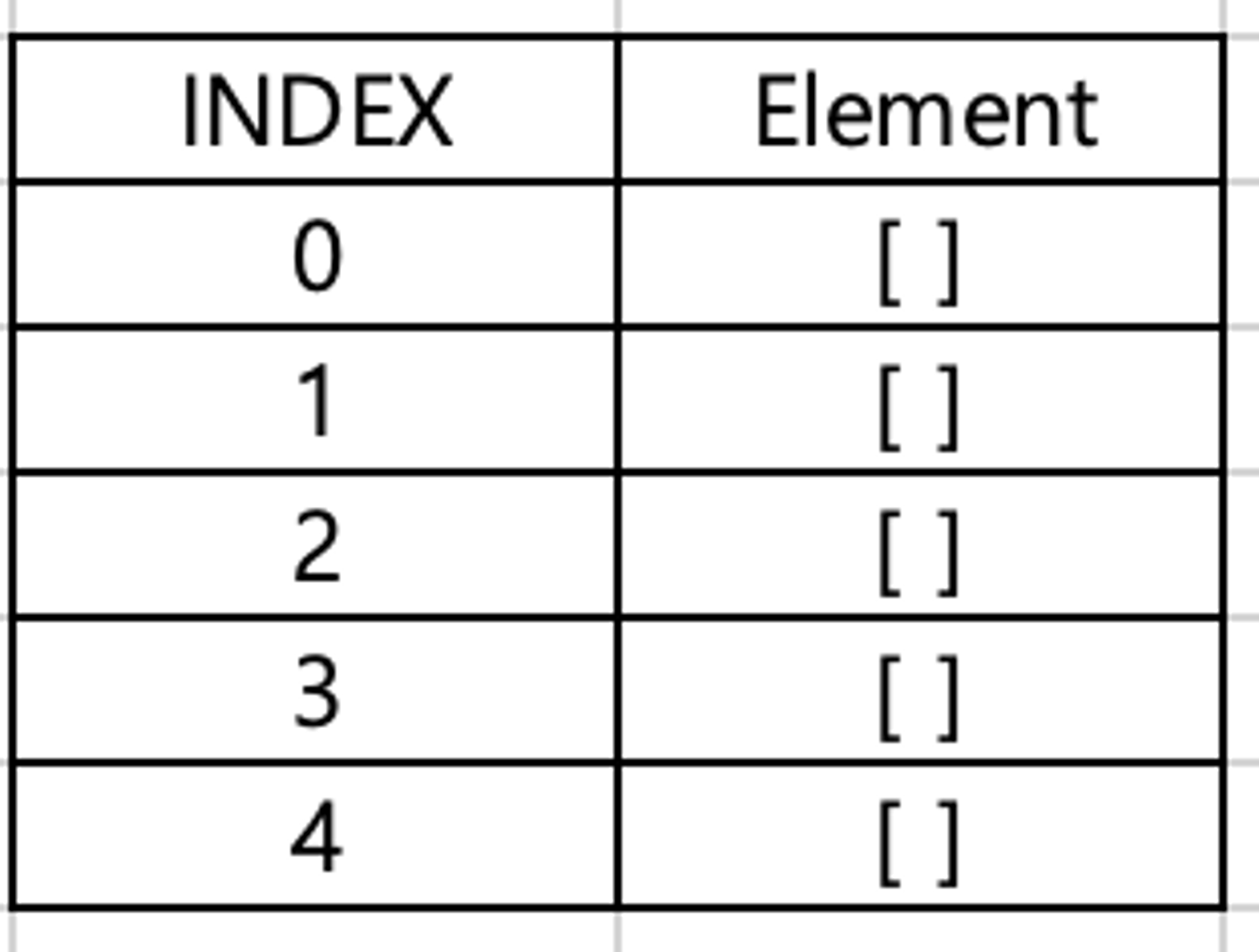
# 5개 노드의 인접 노드 정보를 담을 인접 리스트
SIZE = 5
adjList = [[] for _ in range(SIZE)]
print(adjList)
"""
[[],
[],
[],
[],
[]]
"""언제 사용하나?
- 그래프가 희소한(Sparse) 경우 사용한다.
- 간선에 비해 노드의 개수가 상대적으로 많은 경우 유리하다.
장점
- 각 노드에 연결된 간선들을 리스트로 표현하기 때문에 연결된 간선을 찾는데 O(degree)의 시간이 소요되므로, 정점의 이웃을 빠르게 탐색 가능하다.
- 메모리를 효율적으로 사용한다.
단점
- 인접 행렬방식에 비해서 특정 두 정점 간의 연결여부를 찾는 속도가 느리다.
인접 행렬 선언
- 우선 초기화 하고자하는 값을 컬럼 크기만큼 가지는 리스트를 하나 만들고 해당 리스트를 로우 사이즈만큼 반복하여 NxM matrix를 만든다.
- 처음보면 어색할수 있으므로 두단계로 나눠서 설명해보았다.

이제 리스트 컴프리헨션을 이용하여 5x7 Matrix를 생성해보자.
# 0으로 초기화 된 5x7 Matrix 생성
ROW_SIZE = 5
COL_SIZE = 7
adjMatrix = [[0 for _ in range(COL_SIZE)] for _ in range(ROW_SIZE)]
print(adjMatrix)
"""
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]]
"""
보기 좋게 표현해보면 아래와 같은 테이블이 만들어진다고 볼 수 있다.
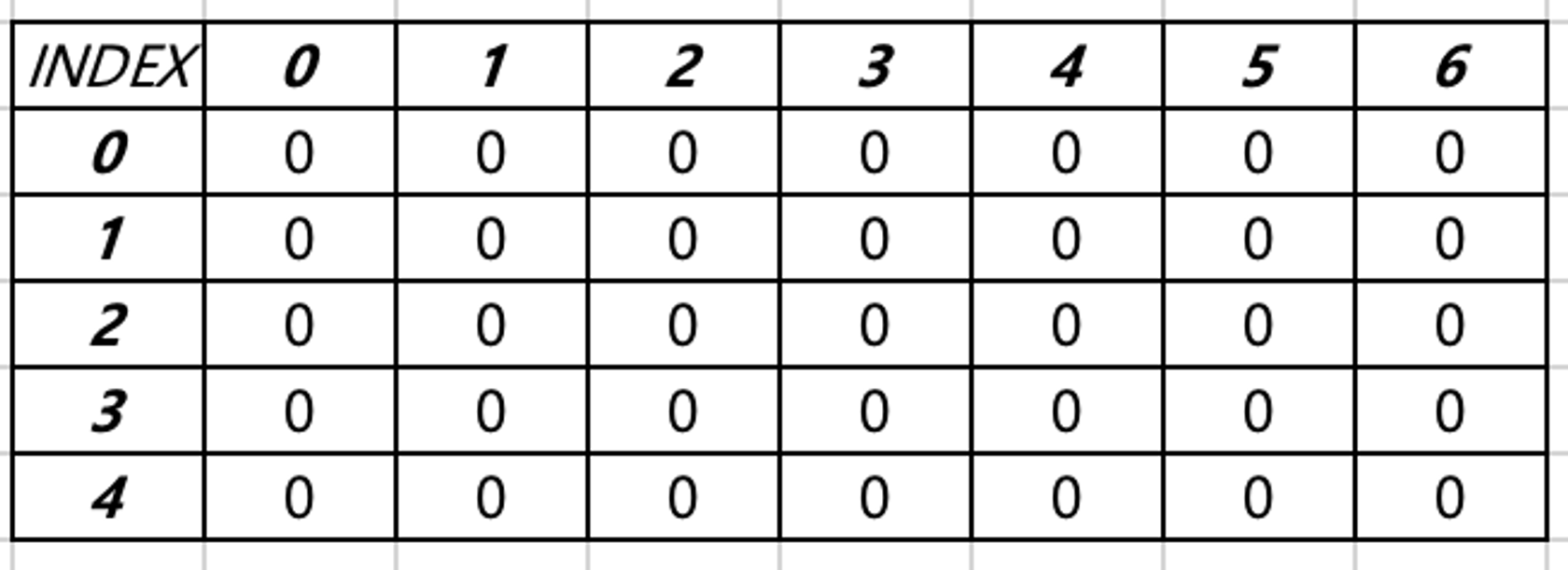
언제 사용하나?
- 그래프가 밀집한 경우(Dense Graph) 인접 행렬이 유용하다.
- 그래프를 구성하는 간선의 수가 정점의 수보다 상대적으로 많을 때 사용한다.
- 미로 찾기와 같이 주어지는 노드들의 구조가 격자 형태의 구조를 가질때 인접행렬로 표현하면 직관적이고 편하다.
장점
- 특정 두 정점간의 연결 여부를 상수 시간(O(1))에 알 수 있다.
- 직관적인 표현을 할 수 있다.
단점
- 노드의 수에 비례하여 메모리 자원을 많이 소모하게 된다.
- 그래프가 희소한 경우 사용되지 않는 메모리가 많아져서 불필요한 메모리 낭비가 발생할 수 있다.
