정렬(Sorting)

이름	평균 시간복잡도	최악 시간복잡도	Stability	In-place	활용 상황
Bubble sort	O(n2)	O(n2)	stable	in-place
Selection sort	O(n2)	O(n2)	unstable	in-place	작은 배열에서, 쓰기(swap) 비용이 클 때 활용
Insertion sort	O(n2)	O(n2)	stable	in-place	일반적으로 작은 배열에서 활용
Quick sort	O(nlgn)	O(n2)	unstable	in-place	원시 타입 배열에서, 최악 상황을 피할 수 있을 때 활용
Merge sort	O(nlgn)	O(nlgn)	stable	not in-place	참조 타입 배열에서 활용
Heap sort	O(nlgn)	O(nlgn)	unstable	in-place	원시 타입 배열에서, 자원적 한계가 클 때 활용
Counting sort	O(n+k)	O(n+k)	stable	not in-place	원소의 종류가 한정적일 때 활용
Radix sort	O(w·n)	O(w·n)	LSD: stable MSD: unstable	not in-place	자릿수가 있는, 이진 문자열이나 정수를 정렬할 때 활용

Quadratic sorts

평균 O(n2)의 시간복잡도를 갖는 정렬 알고리즘들

• 최선의 상황에 O(1)의 시간복잡도를 가진다는 장점이 있음
• 구현이 간단하여 크기가 매우 작은(10~20) 배열에서는 분할 정복 정렬들보다 빠르게 작동함

Bubble sort

각 원소에 대해서, 뒤로 가야하는 만큼 Swap을 거쳐 정렬하는 알고리즘

• 일반적으로 다른 정렬 알고리즘에 비해 성능이 떨어짐

Selection sort

각 인덱스에 대해서, 뒤의 원소들 중 최소값을 골라 Swap하여 정렬하는 알고리즘

• 거리가 먼 원소들을 Swap하므로 기존 순서가 바뀔 수 있음 (unstable)
• 일반적으로 Insertion sort에 비해 성능이 떨어지나, Swap 횟수가 더 적기 때문에 쓰기 비용이 클 때 사용함

Insertion sort

각 원소에 대해서, 앞의 원소들 중 자신보다 작은 값이 나올 때까지 Swap하여 정렬하는 알고리즘

• O(n2)이지만, 구현이 간단하여 크기가 매우 작은(10~20) 배열에서는 분할 정복 정렬들보다 빠르게 작동함
• 일반적으로 Selection sort에 비해 확인해야 할 원소 수가 적으므로, 비교적 성능이 좋음

O(nlgn) sorts

평균 O(nlgn)의 시간복잡도를 갖는 정렬 알고리즘들

• 구현이 복잡하지만, 일반적인 상황에서 가장 빠름

Quick sort

원소 중 하나를 피벗(pivot)으로 고르고, 피벗 앞에는 작은 값들이, 뒤에는 큰 값들이 오도록 하며, 피벗을 기준으로 분할하여 재귀적으로 정렬하는 알고리즘

• 거리가 먼 원소들을 Swap하므로 기존 순서가 바뀔 수 있음 (unstable)
• 추가 메모리를 적게 사용하므로, CPU 캐시 효율이 높음 (in-place)
• 배열이 이미 정렬되어 있을 때에는 O(n2)의 시간복잡도를 냄
  • 이는 좋은 pivot 알고리즘을 사용함으로써 회피할 수 있음
  • 단, 구현이 복잡해져 성능에 영향을 주므로, 작은 크기의 배열에는 Insertion sort를 사용하여 해결함

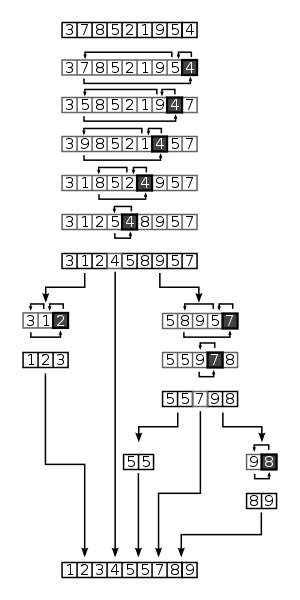
Merge sort

배열을 반씩 재귀적으로 나누고, 가장 작은 단위부터 차례대로 병합하여 정렬하는 알고리즘

• 원소를 하나씩 병합하므로 기존 순서가 바뀌지 않음 (stable)
• 분할로 인해 추가 메모리를 많이 사용하므로, CPU 캐시 효율이 낮음 (not in-place)

Heap sort

힙 자료 구조에 원소를 넣고 빼는 개념을 활용하여 정렬하는 알고리즘

• 추가 메모리를 덜 사용하는 in-place 알고리즘이므로, CPU 캐시 효율이 높음
• 최악의 경우에도 O(nlgn)의 시간복잡도를 내므로 Quick sort에 비해 안전하나, CPU 캐시 효율이 비교적 낮음
• 병렬 처리가 어려움

Non-comparative sorts

원소 간 비교 없이, O(n)의 시간복잡도를 갖는 정렬 알고리즘들

• 추가 메모리를 사용해야 하므로

Counting sort

원소의 종류마다 세어서 개수 순으로 정렬하는 알고리즘

• 뒤에서부터 정렬함으로써 기존 순서를 지킴 (stable)
• 원소의 종류가 많을 수록 비효율적임

Radix sort

원소의 각 자릿수 기준 정렬을 반복하여 정렬하는 알고리즘

• LSD(Least significant digit): 낮은 자릿수부터 확인함
  • 자릿수 차이가 큰 경우, 보는 자릿수가 높아질 수록 봐야할 원소 수가 줄어드므로 비교적 빠름
• MSD(Most significant digit): 높은 자릿수부터 확인함
  • 자릿수가 정해진 경우, 단번에 많은 원소를 정렬하므로 비교적 빠름

분할 정복(Divide-and-conquer)

문제를 작은 문제들로 재귀적으로 분할함으로써 간단히하여 해결하는 알고리즘 설계 전략

• 하위 문제의 최적해를 결합하여 해결
• 예시: Merge sort, Quick sort

Dynamic programming

수학적 최적화와 컴퓨터 프로그래밍을 통한 알고리즘 설계 전략

• 하위 문제의 최적해로 상위 문제의 최적해를 결정
• Memoization: 각 연산에 대한 결과를 저장하여 나중에 활용함 (중복 계산 방지)
• 접근법:
  • Top-down: 상위 문제를 해결하기 위해 하위 문제에 대해 재귀 호출
  • Bottom-up: 하위 문제부터 풀어가면서 상위 문제까지 최적해를 쌓아감
• 예시: 피보나치 수열, 0-1 Knapsack problem, Floyd-warshall algorithm

Greedy algorithm

각 단계마다 순간적으로 최적인 선택을 이어가는 알고리즘

• 일반적으로 최종적인 최적해를 내지는 않고, 합리적인 시간 내에 근사적인 최적해를 내기 위해 활용함
• 예시: Prim's algorithm, Kruskal's algorithm

Prim's algorithm

가장 가까운 노드를 선택해가면서 최소 스패닝 트리를 구하는 알고리즘

• Dijkstra's algorithm을 통해 가까운 노드 순으로 선택함
• 모든 노드를 살펴보므로, 간선이 더 많은 밀집 그래프에 적합함
  • 시간복잡도 O(V2)
  • 바이너리 힙과 인접 리스트를 활용하면 O(ElgV)
  • Dijkstra's algorithm과 시간복잡도가 같음

Kruskal's algorithm

가장 짧은 간선을 선택해가면서 최소 스패닝 트리를 구하는 알고리즘

• Disjoint-set 자료 구조를 통해 사이클을 검사함
• 모든 간선을 살펴보므로, 노드가 더 많은 희소 그래프에 적합함
  • 시간복잡도 O(ElgE)
  • 이는 O(VlgV)와 O(V2lgV)의 사이임 (∵ V-1 ≤ E ≤ V(V-1)/2)

Backtracking

function backtrack(c):
    if reject(P, c) then return
    if accept(P, c) then output(P, c)
    s := first(P, c)
    while s ≠ NULL do
        backtrack(s)
        s ← next(P, s)

조건을 만족하는 해들을 구하기 위해, 유망한 후보들을 점진적으로 검사하는 알고리즘

• 후보가 유망한지 알 수 있는 문제에 적합함
• Brute-force search에 비해 후보 수를 크게 줄이므로 효율적임
• 상태 공간을 DFS로 살펴봄으로써 해결함
• 예시: Eight queens puzzle, Crosswords

Branch and bound

하나의 최적해를 구하기 위해, 제한 범위 내의 후보들을 점진적으로 검사하는 알고리즘

• 상태에 대한 하한(lower bound) 혹은 상한(upper bound)을 결정할 수 있는 문제에 적합함
• 상태 공간을 BFS 혹은 Best-first search로 살펴봄으로써 해결함
• 예시: Dijkstria's algorithm

Shortest path problem

노드 간 최단 거리를 구하는 알고리즘

Dijkstra's algorithm

음의 가중치가 없는 그래프에서, 한 노드에서 다른 모든 노드로의 최단 비용(SSP)을 구하는 알고리즘

• 시간복잡도 O(V2)
• 바이너리 힙과 인접 리스트를 사용하면 O(ElgV)

function Dijkstra(Graph, source):
    dist[source] ← 0                           // 출발 정점에 대해 초기화

    create vertex priority queue Q             // 거리에 대한 Min-heap

    for each vertex v in Graph:
        if v ≠ source
            dist[v] := INF

        Q.add(v, dist[v])

    while Q is not empty:
        (u, cost) := Q.extract_min()             // 다음으로 가장 빠른 정점
        if dist[u] > cost                      // 갱신되었다면 무시함
            continue
        
        for each neighbor v of u:
            alt := dist[u] + length(u, v)
            if alt < dist[v]
                dist[v] := alt                 // 이미 큐에 있는 v들은 앞으로 무시될 것임
                Q.add(v, alt)

    return dist

Bellman-ford algorithm

음수 사이클이 없는 그래프에서, 한 노드에서 다른 모든 노드로의 최단 비용(SSP)을 구하는 알고리즘

• 시간복잡도 O(VE)
• 음의 가중치가 있는 그래프에서 활용할 수 있음

function BellmanFord(list vertices, list edges, vertex source):
    dist := list of size n

    // Step 1: 초기화
    for each vertex v in vertices:
        dist[v] := INF
    
    dist[source] := 0              // 출발 정점에 대해 초기화

    // Step 2: 완화(Relaxation)
    repeat |V|−1 times:
        for each edge (u, v) with weight w in edges:
            if dist[u] + w < dist[v]
                dist[v] := dist[u] + w

    // Step 3: 음수 사이클 확인을 위해 같은 내용 한 번 더 실행
    for each edge (u, v) with weight w in edges:
        if dist[u] + w < dist[v]
            error "Graph contains a negative-weight cycle"

    return dist

Floyd-warshall algorithm

각 노드에서 다른 모든 노드로의 최단 비용(ASP)을 구하는 알고리즘

• 시간복잡도 O(V3)
• 음수 사이클이 없는 그래프에서만 활용할 수 있음

let dist be a |V| × |V| array of minimum distances initialized to INF

for each edge (u, v):
    dist[u][v] := w(u, v)  // u에서 v로 가는 정점의 가중치
for each vertex v:
    dist[v][v] := 0

for k from 1 to |V|:
    for i from 1 to |V|:
        for j from 1 to |V|:
            if dist[i][j] > dist[i][k] + dist[k][j] 
                dist[i][j] := dist[i][k] + dist[k][j]