Background: Neural machine translation

RNN Encoder-Decoder

Encoder reads the input sentence, a sequence of vectors $\mathbf{x}=(x_1,...,x_{T_x})$, into a vector c. The most common approach is to use an RNN such that

$h_t$ is a hidden state at time t, and c is a vector generated from the sequence of the hidden states. f,q are some nonlinear func.

Decoder is often trained to predict the next word $y_t'$ given the context vector c and all the previously predicted words $y_1,...,y_{t'-1}$
In other words, the decoder defines a probability over the translation y by decomposing the joint probability into the ordered conditionals.

where $\mathbf{y}=(y_1,...,y_{T_y})$. With an RNN, each conditional probability is modeled as

where g is a nonlinear, potentially multi-layered, function that outputs the probability of $y_t$, and $s_t$ is the hidden state of the RNN.

Learning to align and translate

The new architecture consists of a bidirectional RNN as an encoder and decoder that emulates searching through a source sentence during decoding a translation.

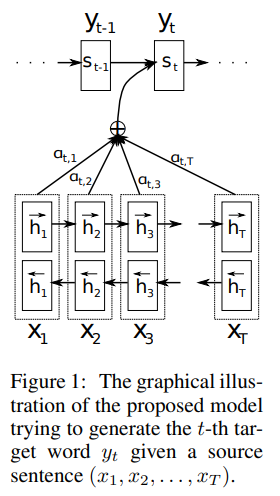
Decoder: General Description

We define each conditional probability into

where $s_i$ is an RNN hidden state for time i, computed by

The difference between existing encoder-decoder approach and ours is the probability is conditioned on a distinct context vector $c_i$ for each target word $y_i$$

The context vector $c_i$ depends on a sequence of annotations$(h_1,...,h_{T_x})$ to which an encoder maps the input sentence. Each annotation $h_i$ contains information about the whole input sequence with a strong focus on the parts surrounding the $i$-th word of the input sequence.

The context vector $c_i$ is computed as a weighted wum of these annotations $h_i$:

The weight $\alpha_{ij}$ of each annotation $h_j$ is computed by

where $e_{ij}=a(s_{i-1},h_j)$, $a$ is an alignment model which scores how well inputs around position $j$ and the output at position $i$ match. The score is based on the RNN hidden state $s_{i-1}$ and the $j$-th annotation $h_j$ of the input sentence.
The probability $\alpha_{ij}$,or its associated energy $e{ij}$, reflects the importance of the annotation $h_j$ with respect to the previous hidden state $s_{i-1}$ in deciding the next state $s_i$ and generating $y_i$.

The decoder decides parts of the source sentence to pay attention to.

This attention mechanism, we relieve the encoder from burden of having to encode all information can be spread throughout the sequence fo annotations.

Encoder: Bidirectional RNN for annotating sequences

A BiRNN consists of forward and backward RNN's. We obtain an annotation for each word $x_j$ by concatenating the forward hidden state$\overrightarrow{h}_j$ and the backward one $\overleftarrow{h}_j$, i.e., $h_j=\lbrack \overrightarrow{h}_j^{\top};\overleftarrow{h}_j^{\top}\rbrack{}^{\top}$
In this way, the annotation $h_j$ contains the summaries of both the preceding words and the following words. Due to the tendency of RNNs to better represent recent inputs, the annotation $h_j$ will be focused on the words around $x_j$.