Introduction

Image to Image Translation

• 한 이미지의 domain을 다른 domain으로 변환하는 것을 목표로 하는 생성 모델의 한 분야
  • 흑백이미지를 컬러 이미지, 낮 사진을 밤 사진으로 변환
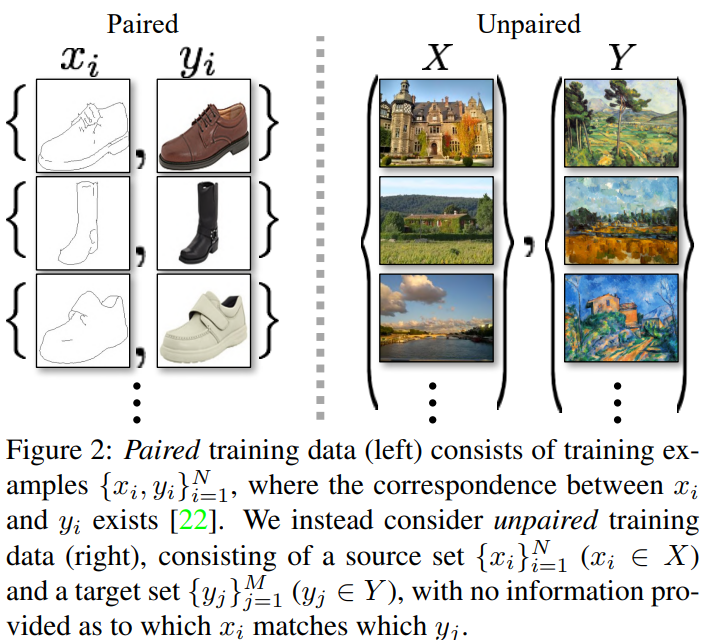
• 기존 Image to Image Translation은 paired data를 가지고 수행해야 결과가 좋았음
• Unpaired data를 가지고 GAN의 loss function 하나로 진행할 경우 ModeCollapse가 발생하는 문제가 있음
• 위 두가지 문제를 해결하기 위해 기존 GAN에 Cycle Consistency를 도입
  

Related Work

• GAN의 구조

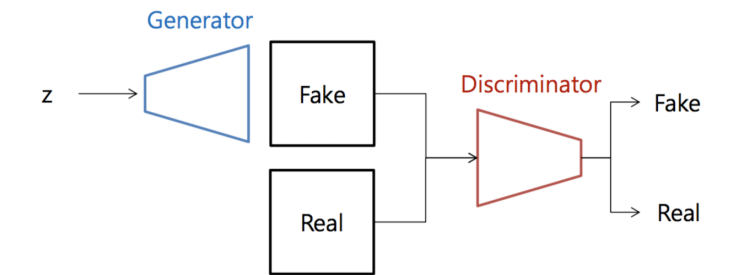
• Adversarial Loss
  $\min_G \max_D V(D,G)=E_{x~p_{data}(x)}[log\, D(x)]+E_{z~p_z(z)}[log(1-D(G(z))]$
• 위 loss를 통해 Generator가 실제 데이터 분포와 비슷한 데이터를 생성하도록 학습할 수 있음
  
• Pix2Pix(cGAN)
  • 문제점: paired 데이터를 필요로 함
• CoGAN
  • 문제점: 모델이 사전 정의된 유사성 함수에 의존하거나 입력과 출력이 동일한 low-dimensional embedding space에 있다는 가정을 만족해야함
• Cycle Consistency
  
  • Translation is cycle consistent??
    • 어떠한 데이터 x를 가지고 translation한 결과값 $\hat y$라면 $\hat y$를 다시 x로 translation할 경우 x가 나오는 것
    • 영어로 된 문장을 한국어로 번역했을 때 해당 한국어를 다시 영어로 번역 시 본래의 영어 문장에 도출되는것을 말함

Formulation

Adversarial Loss

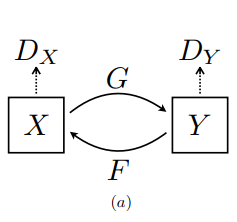
• 정방향
  $G:x\rarr y\\ L_{GAN}(G,D_Y,X,Y)=\Bbb E_{y~p_{data}(y)}[log\,D_Y(y)]+\Bbb E_{x~p_{data}(x)}[log\,1-D_Y(G(x))]$
• 역방향
  $F:y\rarr x\\ L_{GAN}(F,D_X,Y,X)=\Bbb E_{x~p_{data}(x)}[log\,D_X(x)]+\Bbb E_{y~p_{data}(y)}[log\,1-D_X(F(y))]$

Cycle Consistency Loss

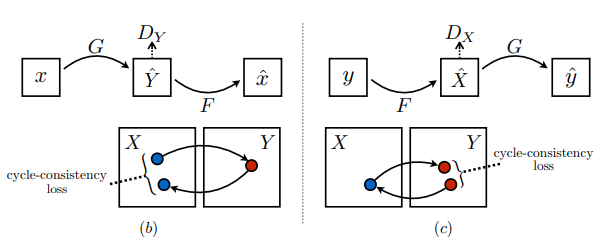
• 각각의 Translator G와 F에 대해 원본을 복원하는 능력을 향상시키는 Ctcle Consistency Loss

• 해당 loss를 통해 output을 다시 input으로 대응할 수 있게끔 학습하면서 다양성을 최대한으로 제공하게 됨

• 최종 손실 함수

  $L(G,F,D_X,D_Y)=L_{GAN}(G,D_Y,X,Y)+L_{GAN}(F,D_X,Y,X)+\lambda L_{cyc}(G,F)$

Results