다익스트라(Dijkstra)

가중치 그래프에서 시작점과 도착점이 주어졌을 때, 최소 비용을 return하는 알고리즘이다.

---

다익스트라의 원리

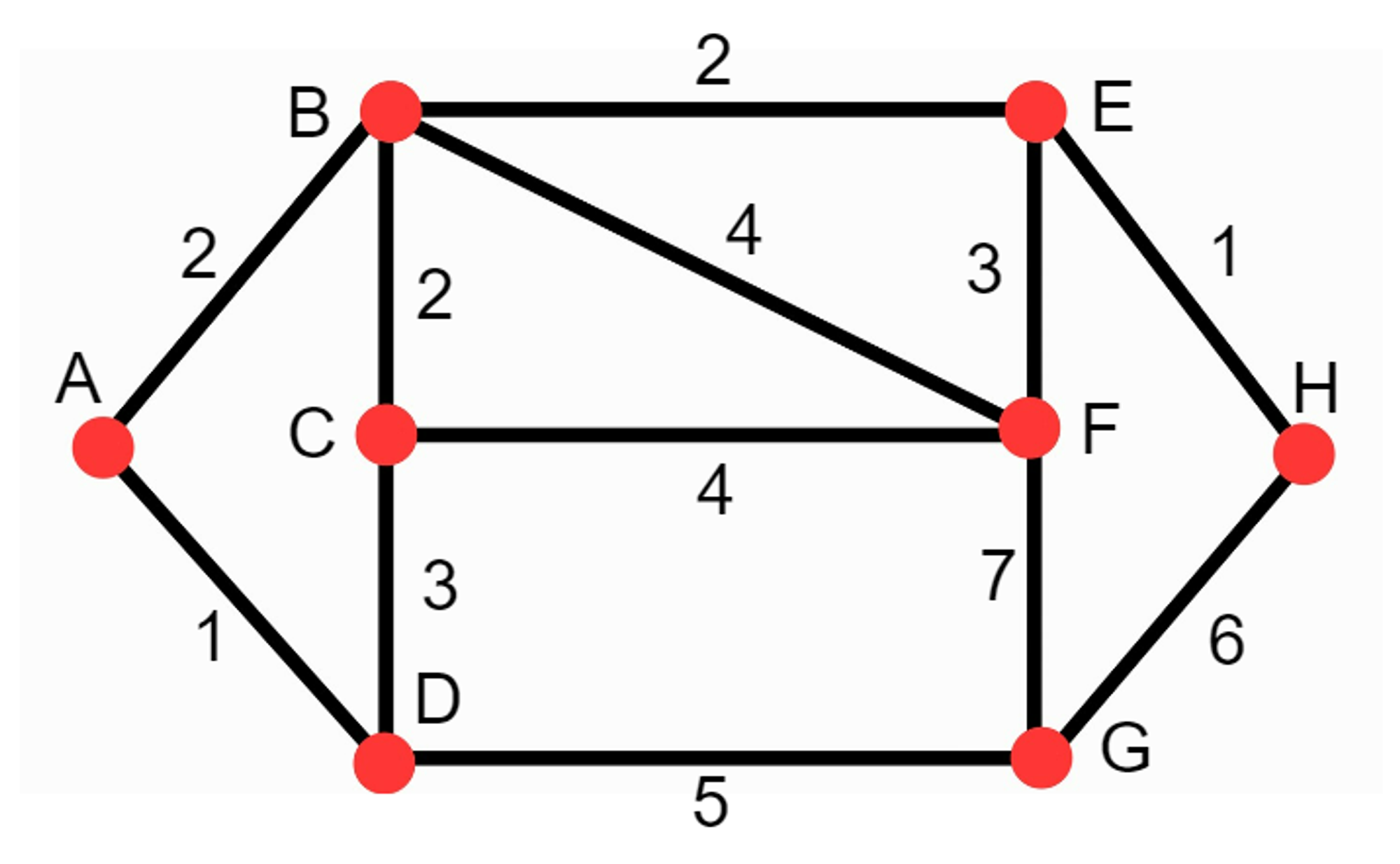
위 사진과 같은 가중치 그래프가 주어지고 시작점은 A, 도착점은 H라고 가정한다.
1. 각각의 점에 라벨을 매겨준다. 시작점의 라벨은 0으로 초기화하고 나머지 점들은 ∞로 초기화한다.
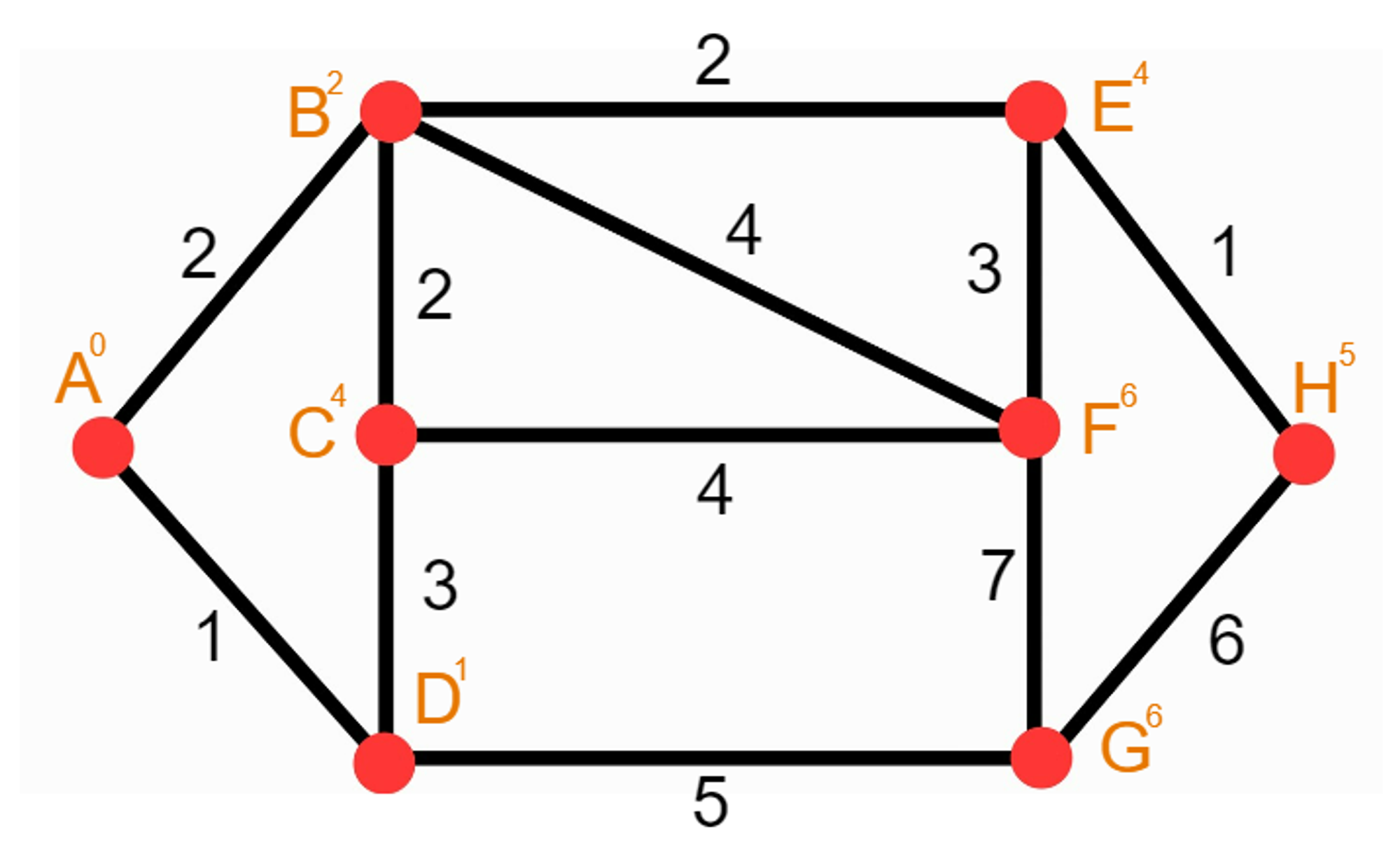
2. 사용 안 한 라벨 중 제일 작은 라벨을 찾고, 해당 라벨을 사용했다고 표시해준다.
3. 해당 점에 인접한 점들의 라벨들을 업데이트 해준다.
(이미 라벨이 되어 있는 값보다 작으면 작은 값으로 업데이트 해주고, 크면 업데이트 하지 않는다.)
4. 2-3의 과정을 반복하고 모든 라벨을 사용했으면 종료한다.

---

다익스트라 구현

1. 그래프 구현

const graph = {
    "A": [("B", 2), ("D", 1)],
    "B": [("C", 2), ("E", 2), ("F", 4)],
    "C": [("F", 4)],
    "D": [("G", 5)],
    "E": [("H", 1)],
    "F": [("E", 3)],
    "G": [("F", 7), ("H", 6)],
    "H": [],
}

2. distance 구현

const INF = 1e9;
const numV = Object.keys(graph).length;
const distance = Array(numV + 1).fill(INF);

3. heap 구현

distance[start] = 0;

---

전체 코드

class MinHeap {
    constructor() {
        this.heap = [];
    }

    size() {
        return this.heap.length;
    }

    swap(idx1, idx2) {
        [this.heap[idx1], this.heap[idx2]] = [this.heap[idx2], this.heap[idx1]];
    }

    add(value) {
        this.heap.push(value);
        this.bubbleUp();
    }

    poll() {
        if (this.heap.length === 1) {
            return this.heap.pop();
        }
        const value = this.heap[0];
        this.heap[0] = this.heap.pop();
        this.bubbleDown();
        return value;
    }

    bubbleUp() {
        let index = this.heap.length - 1;
        let parentIdx = Math.floor((index - 1) / 2);

        while (this.heap[parentIdx] && this.heap[index][1] < this.heap[parentIdx][1]) {
            this.swap(index, parentIdx);
            index = parentIdx;
            parentIdx = Math.floor((index - 1) / 2);
        }
    }

    bubbleDown() {
        let index = 0;
        let leftIdx = index * 2 + 1;
        let rightIdx = index * 2 + 2;

        while ((this.heap[leftIdx] && this.heap[leftIdx][1] < this.heap[index][1]) ||
            (this.heap[rightIdx] && this.heap[rightIdx][1] < this.heap[index][1])) {
            let smallerIdx = leftIdx;

            if (this.heap[rightIdx] && this.heap[rightIdx][1] < this.heap[smallerIdx][1]) {
                smallerIdx = rightIdx;
            }

            this.swap(index, smallerIdx);
            index = smallerIdx;
            leftIdx = index * 2 + 1;
            rightIdx = index * 2 + 2;
        }
    }
}

function dijkstra(graph, start, end) {
    const vertex = Object.keys(graph).length;
    const distance = Array(vertex + 1).fill(Number.POSITIVE_INFINITY);
    distance[start] = 0;

    const minHeap = new MinHeap();
    minHeap.add([0, start]);

    while (minHeap.size() > 0) {
        const [dist, now] = minHeap.poll();

        if (distance[now] < dist) {
            continue;
        }

        for (const [vv, ww] of graph[now]) {
            const cost = distance[now] + ww;

            if (cost < distance[vv]) {
                distance[vv] = cost;
                minHeap.add([cost, vv]);
            }
        }
    }

    return distance[end];
}