[자료구조/ 알고리즘] 시간복잡도

우혁·2024년 1월 11일

자료구조/ 알고리즘

목록 보기

1/10

🔐 알고리즘

어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법: 문제를 해결하는 방법

한 문제를 해결하는 방법은 한 가지만 있는게 아니라 무수히 많을 수 있다.

자주 쓰이는 문제 해결 방법은 패턴화: BFS, DFS, DP, 다익스트라 등등

각 상황에 적합한 알고리즘을 선택할 수 있어야 한다.

📊 알고리즘 평가기준

1. 시간 복잡도
동일한 코드로 작성되어도 실행환경에 따라서 매번 실행시간이 달라질 수 있다. 하지만 걸리는 시간의 경향성은 계산할 수 있다.

2. 공간 복잡도(메모리)
메모리는 한정적이기 때문에 최대한 적은 용량의 메모리를 사용하는 것이 좋다. 하지만 컴퓨터의 메모리 용량에 커짐에 따라서 메모리를 크게 신경쓰지 않고 알고리즘을 작성하는 경우도 있다.

3. 구현 복잡도
괜찮은 알고리즘을 떠올렸더라도 구현이 너무 복잡하고 알아보기 힘들다면 다시 생각해볼 필요가 있다. 개발자는 대부분의 경우 협업을 해야하고, 구현이 복잡해지면 다른 사람은 물론 미래의 나도 알아볼 수 없다.

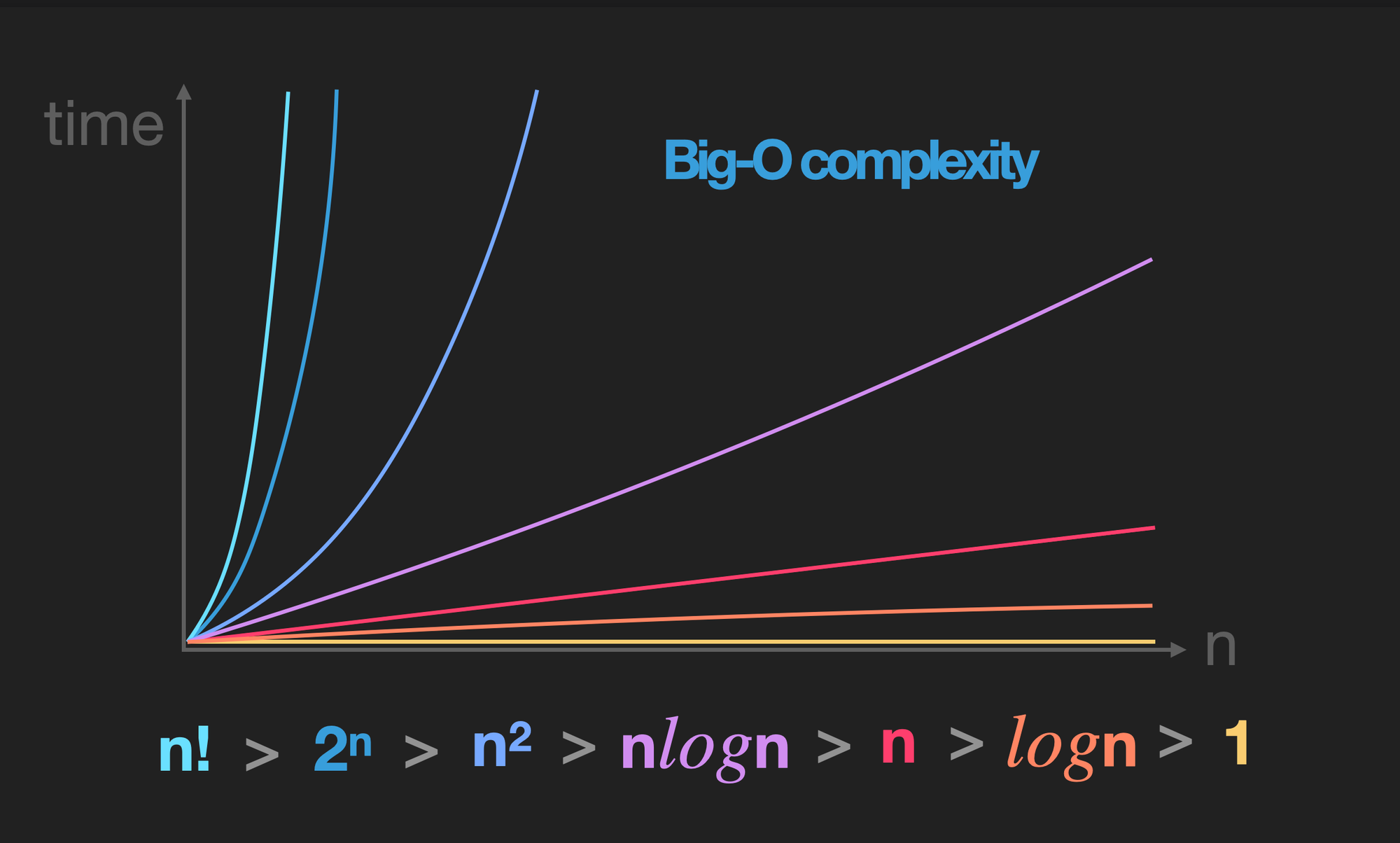
⏳ 시간 복잡도(Big-O)

문제를 해결하는 데 걸리는 시간과 입력값 n의 함수 관계를 말한다.

input n의 크기가 커지면 작은 차수의 항들이 실행시간(Runtime)에 미치는 영향이 미미하다.
⤷ 작은차수 무시, 계수 무시

Big-O를 적용하기 위해서는 최고차항이 무엇인지 판별을 해야하는데 기본적인 것들은 외우는 것이 좋다!

💡 n! > 2ⁿ > n³ > n² > nlogn > n > logn > 1

📝 Big-O의 간단한 예제들

- O(1) 표현식(Simple Statement)

let num = 10;
num += 1;

- O(n) 반복문(Single Loop)

for(let i = 0; i<10; i++){
	console.log(i);
}

- O(n²) 중첩반복문(Nested Loop)

for(let i = 0; i<10; i++){
	for(let j = 0; j<10; j++){
    	console.log("짱구");
    }
}

- O(2ⁿ) 두 번 재호출하는 재귀함수(Recursion)

function fibo(n){
	if(n === 1){
    	return 0;
    }else if(n === 2){
    	return 1;
    }else{
    	return fibo(n - 1) + fibo(n - 2);
    }
}

- O(logn) 탐색해야 하는 데이터가 절반으로 줄어드는 함수 ex)이진탐색 알고리즘

function binarySearch(arr, n, target){
    let start = 0;
    let ent = n;
    let min;
    while(end >= start){
      mid = (end + start) / 2;
      if(arr[mid] === target){
          return 1;
      }else if(arr[mid] > target){
          end = mid - 1;
      }else{
          start = mid + 1;
      }
      return 0;
    }  
}

😟 최악의 상황(worst-case)

Big-O를 이용하여 시간복잡도를 구할 때에는 최악의 상황(worst-case)을 고려해야 한다.

if(true){
	for(let i = 0; i<10; i++){
		console.log(i);
	}
}else{
	for(let i = 0; i<10; i++){
		for(let j = 0; j<10; j++){
    		console.log("짱구");
    	}
	}
}

if문 아니면 else문이 실행되는 데 가장 최악의 경우는 else문이 실행되는 상황이므로 위 코드의 시간복잡도는 O(n²)이다.

💻 코딩테스트를 위한 시간 복잡도

1. sort() O(nlogn)
우리는 정렬을 직접 구현하지 않고 각 언어에서 정의되어 있는 sort()함수를 사용한다.

2. Hashtable 구축: O(n) // Hashtable 검색: O(1)
Hashtable의 강력함은 검색의 시간복잡도가 O(1)라는 점이다. Hashtable은 공간(메모리)를 사용함으로써 시간을 절약하는 방법중에 하나이다. 보통 문제에서 주어지는 크기 n의 배열에 하나 하나 접근하여 hashtable을 구축해야 한다.
이 과정에서 O(n)의 시간복잡도가 걸린다.

3. BinarySearch O(logn)
정렬된 배열에서 특정 숫자를 찾는 알고리즘인 BinarySearch는 코딩테스트 문제에서도 종종 나온다. 반복문 또는 재귀함수가 재호출 될 때마다 탐색해야할 데이터의 크기가 절반씩 줄어들기 때문에 시간복잡도는 O(logn)이 된다.
하지만 정렬이 안되어있는 배열을 주어진다면 정렬sort() O(nlogn)을 먼저 해주어야 한다.

4. Heap(Priority Queue)

길이가 n인 배열을 Heap으로 만들 때 → O(nlogn)
push(), pop() → O(logn)

💻 코딩테스트에서 활용하기!

🚫 제한조건

1. 100,000
문제를 풀다보면 제한사항에 데이터의 크기를 100,000으로 제한한 문제들을 자주 보게 될 것이다.
100,000이라는 숫자에 숨겨져있는 뜻은 다음과 같다.

O(n²)로 풀기는 위험하다.
O(nlogn), O(n), O(logn)의 알고리즘을 생각해야 한다.

2. 비교적 작은 숫자
제한사항에 데이터의 크기를 1,000으로 제한한 문제들도 종종 나온다.

O(n³)로 풀기는 위험하다.
O(n²), O(nlogn), O(n), O(logn)의 알고리즘을 생각해야 한다.

3. 데이터의 크기 제한이 작다면 완전탐색 고려
완전탐색은 무식하게 일일이 다 해보는 방식이기 때문에 시간복잡도가 큰 경우가 많다. 하지만 문제에서 데이터 크기 제한이 작다면, 완전탐색으로 풀어도 된다는 무언의 힌트인 것이다.

4. 순열조합 완전탐색 문제
완전탐색의 연장선상에 있다. 순열조합 문제는 시간복잡도과 굉장히 크기 때문에 작은 크기의 제한사항을 준다.

우혁

🏁

다음 포스트

[자료구조/ 알고리즘] 시간복잡도