소수 판별

📄 소수 (Prime Number)

• 1과 자기자신을 제외하고 약수를 갖지 않는 1보다 큰 자연수

✏️ 시간복잡도 O(N)

• 1과 자기자신을 제외한 숫자로 다 나눠보는 방법

  bool isPrime1(int n) {
  	for (int i = 2; i < n; i++) {
  		if (n % i == 0) {
  			return false;
  		}
  	}
  	// 2 ~ n-1까지 약수가 없다면 소수
  	return true;
  }

✏️ 시간복잡도 O(√N)

• 약수를 구할때, 해당 수의 제곱근을 중심으로 좌측에 있는 수들은 우측에있는 수와 짝을 이룬다.
• 2부터 제곱근까지의 수중, 해당 수와 나누어 떨어지는 수가 있는지 확인, 약수가 있다면 소수가 아니고, 없다면 소수가 된다.
  • 81의 약수는 1, 3, 9, 27, 81
  • 1은 81의 약수이다. 따라서 81/1 = 81 또한 81의 약수이다.
  • 3은 81의 약수이다. 따라서 81/3 = 27 또한 81의 약수이다.
  • 9는 81의 약수이다. 따라서 81/9 = 9 또한 81의 약수이다.
• 소수 판별을 해야할 data 수가 적을 때 효율적

bool isPrime2(int n) {
	// 2 부터 n의 제곱근까지
	for (int i = 2; i <= sqrt(n); i++) {
		if (n % i == 0) {
			return false;
		}
	}
	// 2 ~ n-1까지 약수가 없다면 소수
	return true;
}

✏️ 시간복잡도 O(Nlog(logN))

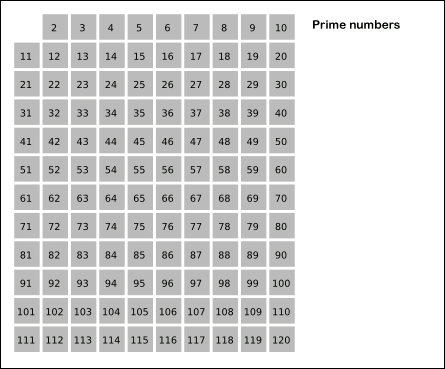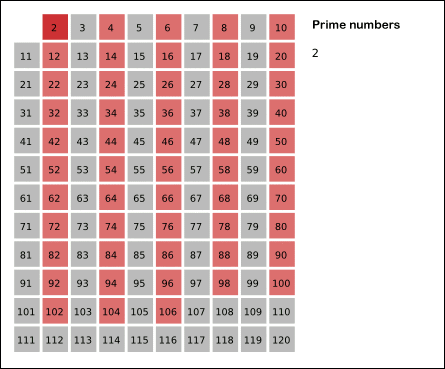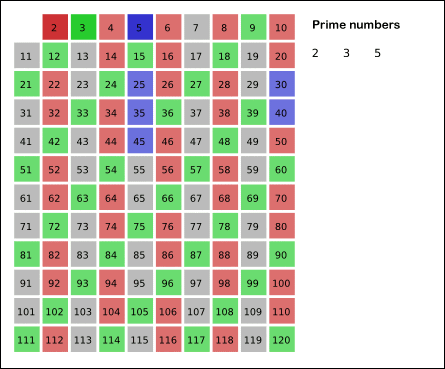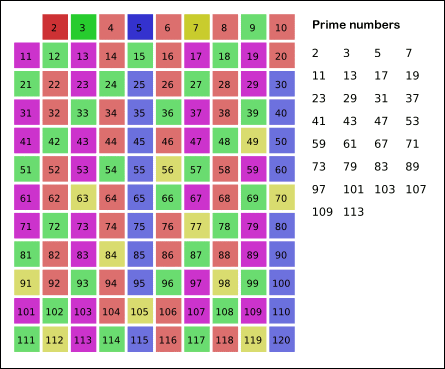
• 에라토스테네스의 체
• 소수 판별을 해야할 data 수가 많을 때 효율적

bool isPrime3(int n) {
	// n까지 구해야하므로, n+1개를 동적할당
	bool* IsPrime = new bool[n+1]; 

	// 처음엔 모두 소수로 보고 true값으로 배열 초기화
	for (int i = 0; i <= n; i++) {
		isPrime[i] = true;
		}
	}

	for (int i = 2; i <= n; i++) {
	    // 만일, PrimeArray[i]가 true이면 i 이후의 i 배수에 대해 false값을 준다
		if (isPrime[i]) { 
			cout << i << " ";
			for (int j = i * 2; j <= n; j +=i) {
				isPrime[j] = false;
			}
		}
	}
}

---

자료 출처

• https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4