시간복잡도

📄 시간복잡도

• 특정 알고리즘이 어떤 문제를 해결하는데 걸리는 시간
• 하지만 시간은 컴퓨터 사양 등 여러가지 요소의 영향을 받는다.
• 따라서 주요 로직의 반복 횟수를 중점으로 시간복잡도를 측정한다.
• 표기법
  • Big-O : 상한 점근 (최악의 경우를 고려한 표기법)
  • Big-Ω : 하한 점근 (최선의 경우를 고려한 표기법)
  • Big-θ : 중간 점근 (최악과 최선의 중간을 고려한 표기법)

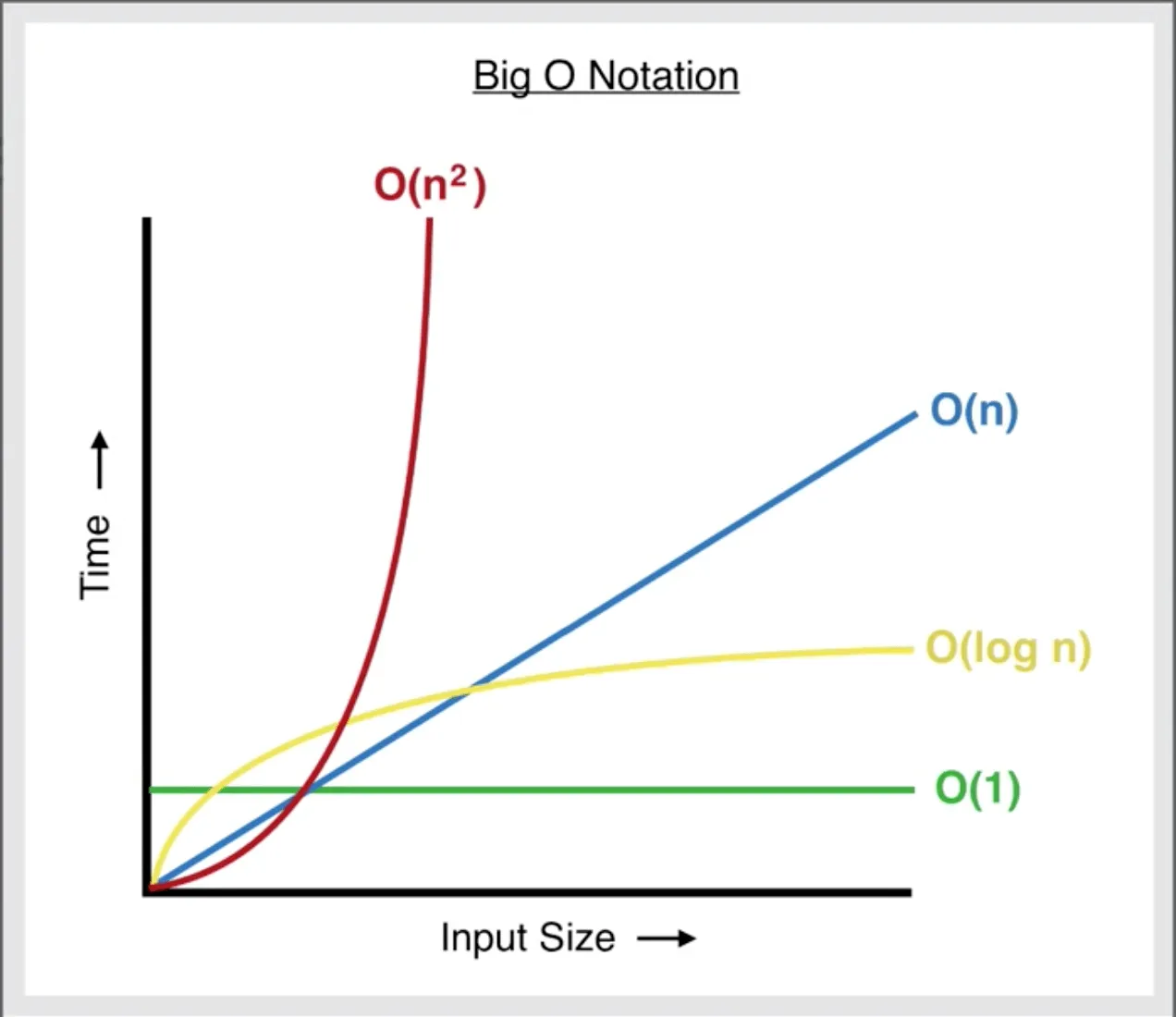
📄 Big-O 표기법

✏️ O(1)

• 일정 복잡도 (Constant complexcity)
• 입력값이 증가하더라도 시간이 늘어나지 않음
• ex) 고정된 데이터를 읽는 경우, 정적인 데이터를 읽는 경우

✏️ O(n)

• 선형 복잡도 (Linear complexity)
• 입력값이 증가함에 따라 시간 또한 같은 비율로 증가
• ex) 1중 for문

✏️ O(log n)

• 로그 복잡도 (Logarithmic complexity)
• 문제를 해결하는데 필요한 단계들이 특정 요인에 의해 연산마다 감소
• ex) BST (Binary Search Tree)

✏️ O(n²)

• 2차 복잡도 (Quardratic complexity)
• 입력값이 증가함에 시간이 n의 제곱수의 비율로 증가
• ex) 2중 for문, 재귀로 구현한 피보나치 수열

✏️ 빠른 순서대로 정렬하시오

• O(1) → O(log n) → O(n) → O(n²) → O(c^N)

---

이미지 출처

• https://levelup.gitconnected.com/big-o-time-complexity-what-it-is-and-why-it-matters-for-your-code-6c08dd97ad59