피보나치 수열

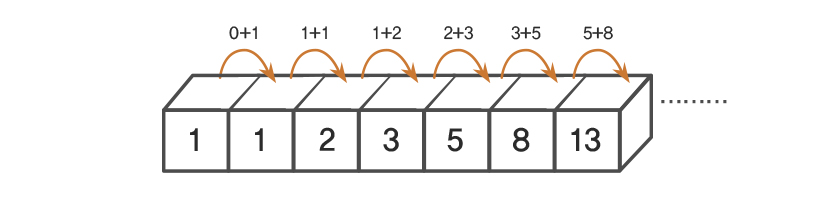
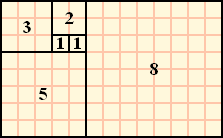
📄 피보나치 수열

• 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열.
  • A(n) = A(n-2) + A(n-1)

✏️ 재귀 함수

• 자기 자신을 재참조하는 함수
• 재귀 함수의 형태
  (1) 종료 조건 : 없을 경우 무한히 반복되므로 기저사례를 써야 함.
  (2) 로직 : 반복문으로 풀 수 있으면 반복문으로 푸는게 낫다.
  (3) 재귀 호출 : 반드시 순환되지 않아야함.
• 오버헤드, 중복 호출이 발생하여 큰 수를 입력했을 때 매우 느림.
  • Big-O 표기법 : O(n³)

int fibo(int n)
{
    if (n == 1 || n == 2)
        return 1;
    else
        return fibo(n-1) + fibo(n-2);
}

✏️ Top-down 방식

1) 큰 문제를 작은 문제로 나눈다.
2) 이미 구한 값이라면 저장한 값을 이용하고, 구해놓지 않은 값이라면 메모이제이션 배열에 저장한다.
3) 작은 문제의 답을 결합해 큰 문제를 해결한다.

• 동적 계획법(Dynamic Programming) : 복잡한 문제를 여러 개의 간단한 문제(하위 문제)로 나누어 풀고, 그것을 결합하여 최종적인 문제를 해결
• 메모이제이션(Memoization) : 동일한 문제를 반복해야 할 경우, 미리 계산해서 저장해 둔 결과를 활용하여 중복 연산을 줄이는 방식

int dp[100] = { 0 };    // 하위 문제 답을 저장할 메모이제이션 배열 

int fibo(int n) 
{
	if (dp[n] != 0)		// 계산한 적이 있는 경우 
    {
    	return dp[n];
    }
    else				// 처음 계산하는 경우
    {
    	if (n == 1 || n == 2) 
        {
        	dp[n] = 1;
        }
        else
        {
        	dp[n] = fibo(n-1) + fibo(n-2);
        }
        return dp[n];
    }
}

int main()
{
    printf("%d", fibo(5));
    return 0;
}

✏️ Bottom-up 방식

1) 작은 문제들부터 푼다.
2) 작은 문제들의 답을 이용해 큰 문제를 푼다.
3) 이를 반복해 최종 문제를 푼다.

int dp[100] = { 0 };    // 하위 문제 답을 저장할 메모이제이션 배열 

int fibo(int n) 
{
    dp[0] = 0;
    dp[1] = 1;
    int i;
    for (i=2; i<=n; i++)    // 2부터 시작해서 n까지 반복
    {    
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

int main()
{
    printf("%d", fibo(5));
    return 0;
}