순회 (Traversal)

순회는 그래프 또는 트리처럼 연결되어 있는 구조에서 노드를 한번씩 탐색하는 것으로 모든 노드 또는 특정 노드를 방문하는 방법을 찾는 것이 목적이다.

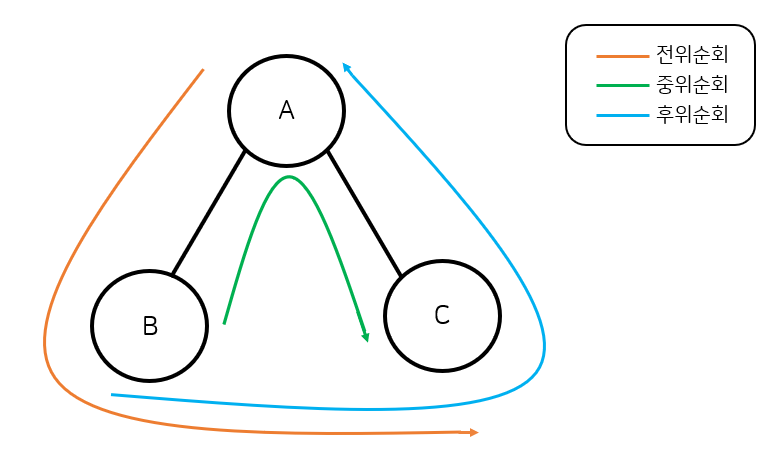
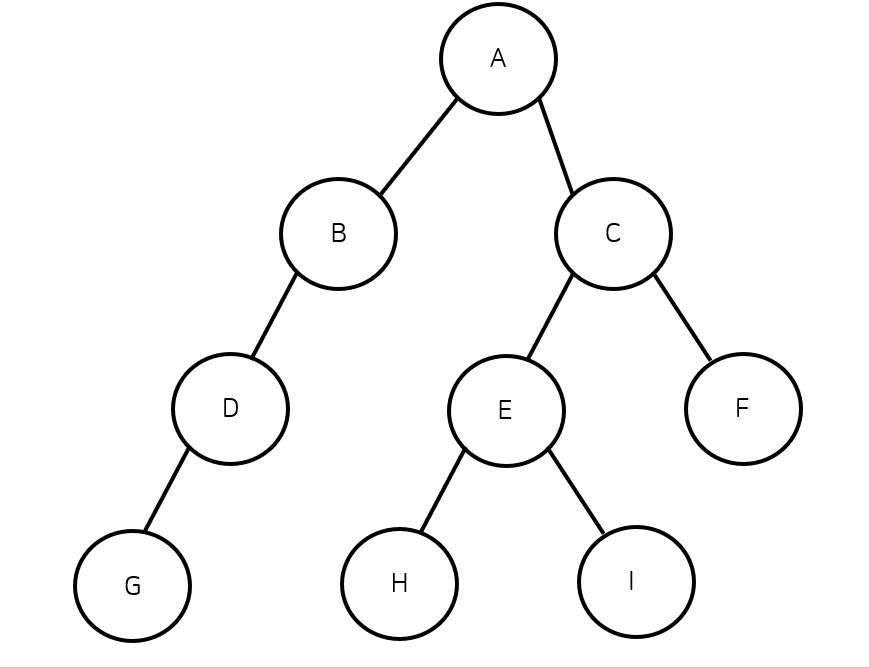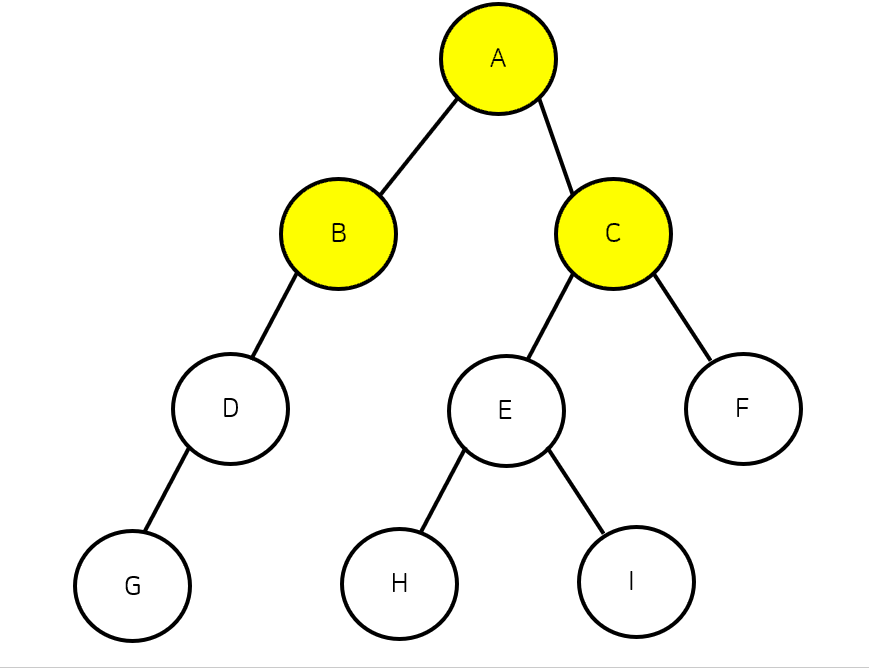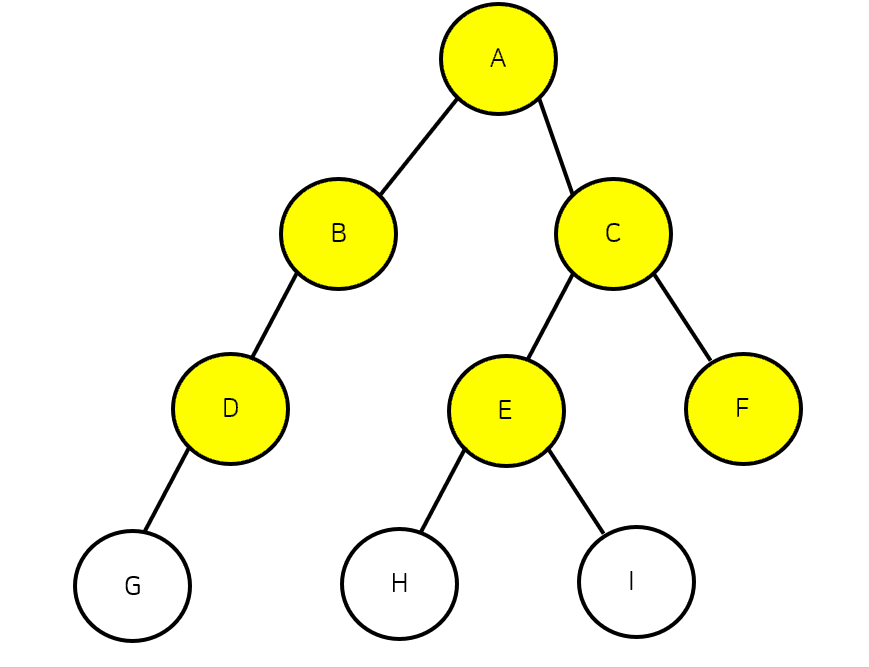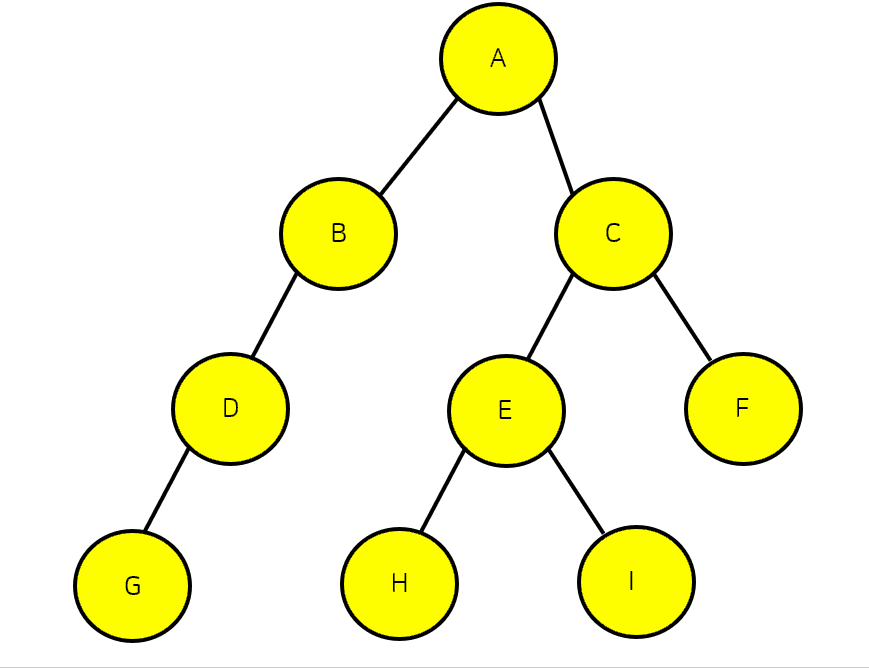
트리의 순회의 경우 위의 사진처럼 전위, 중위, 후위순회로 나눌 수 있다.

전위순회 (preorder travers)

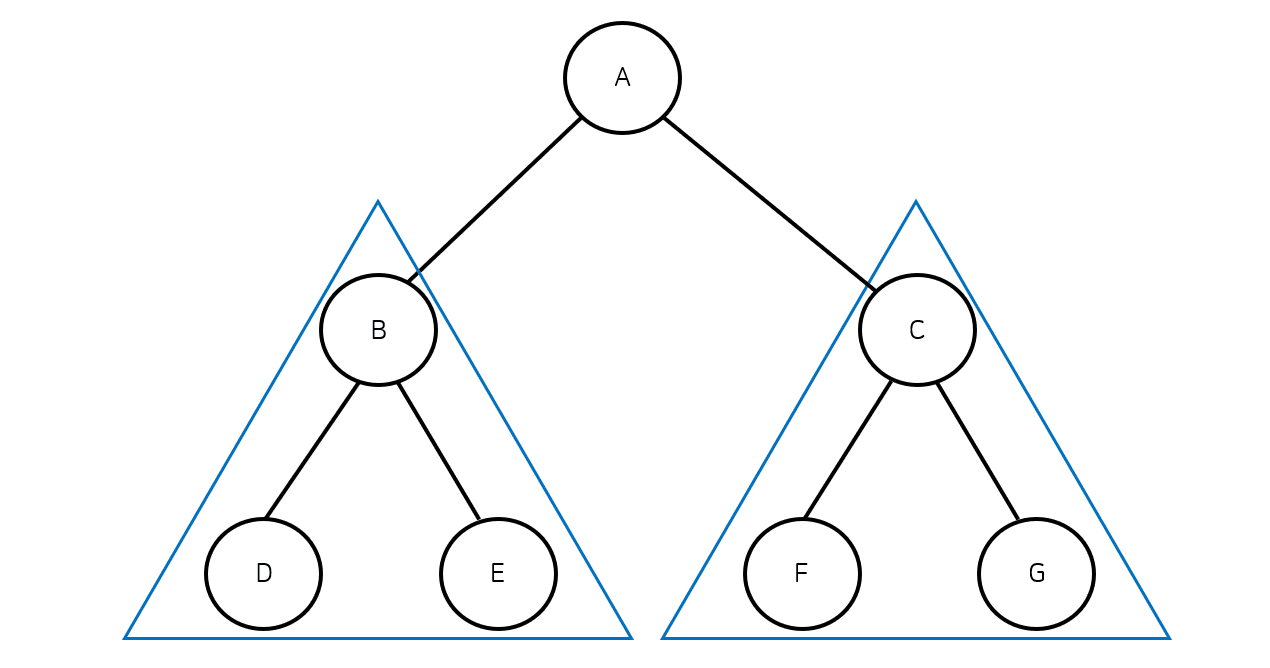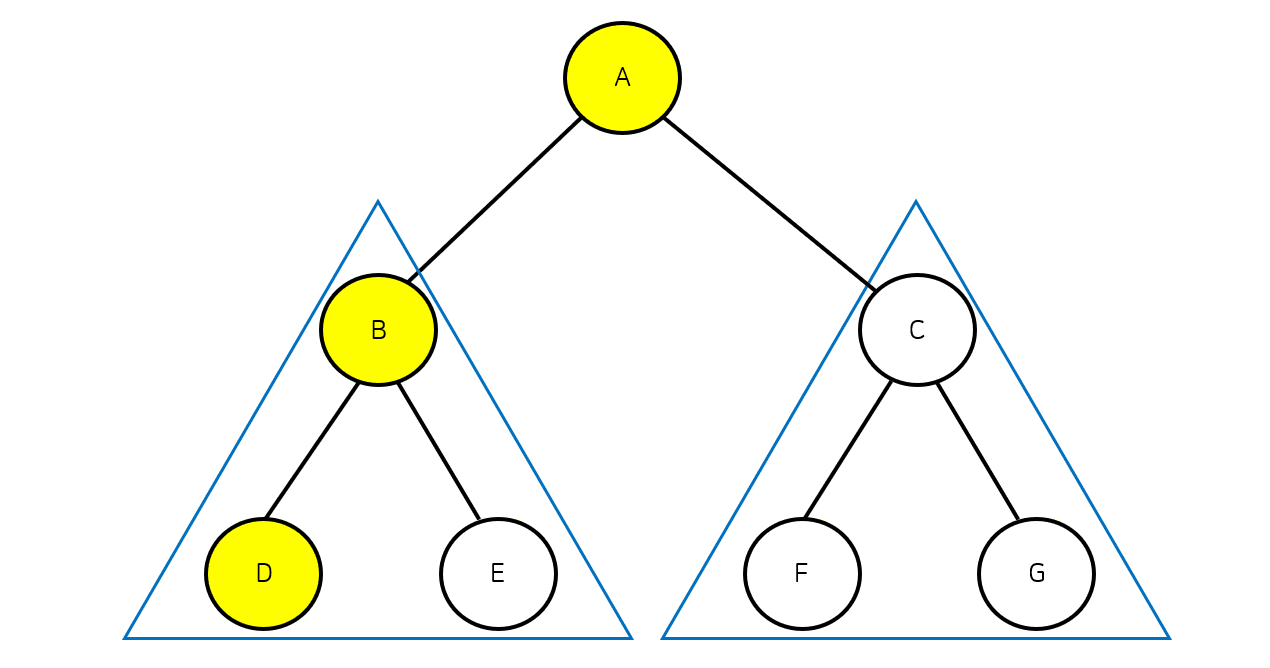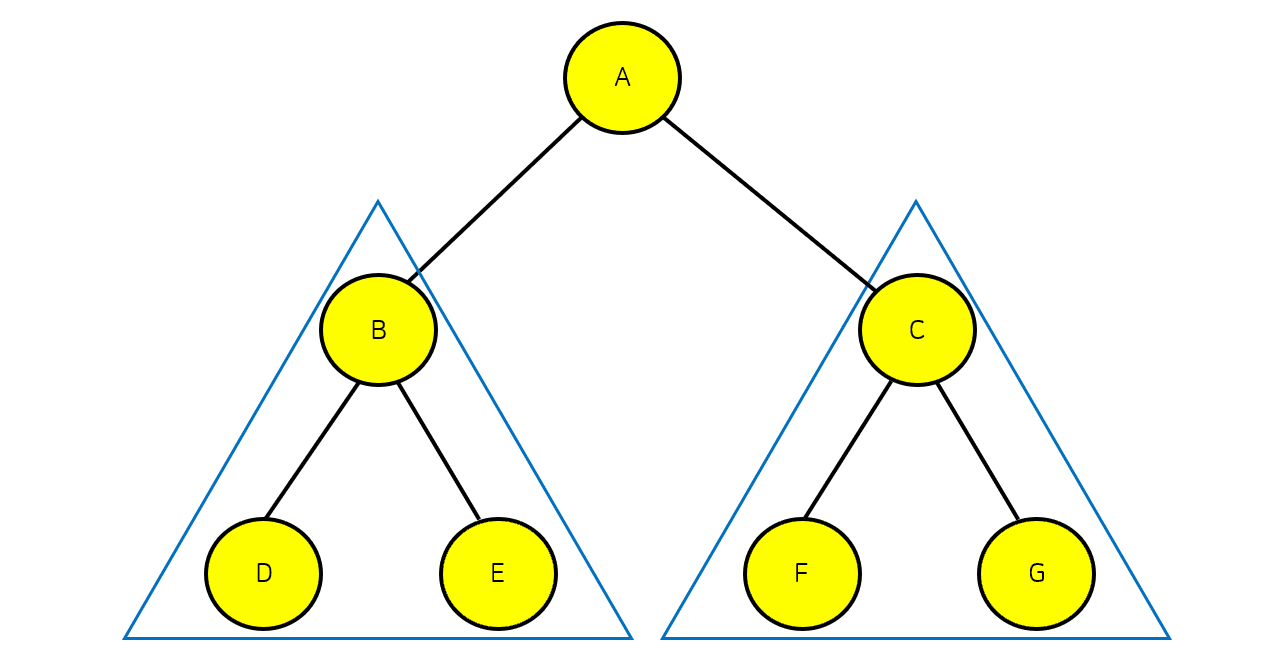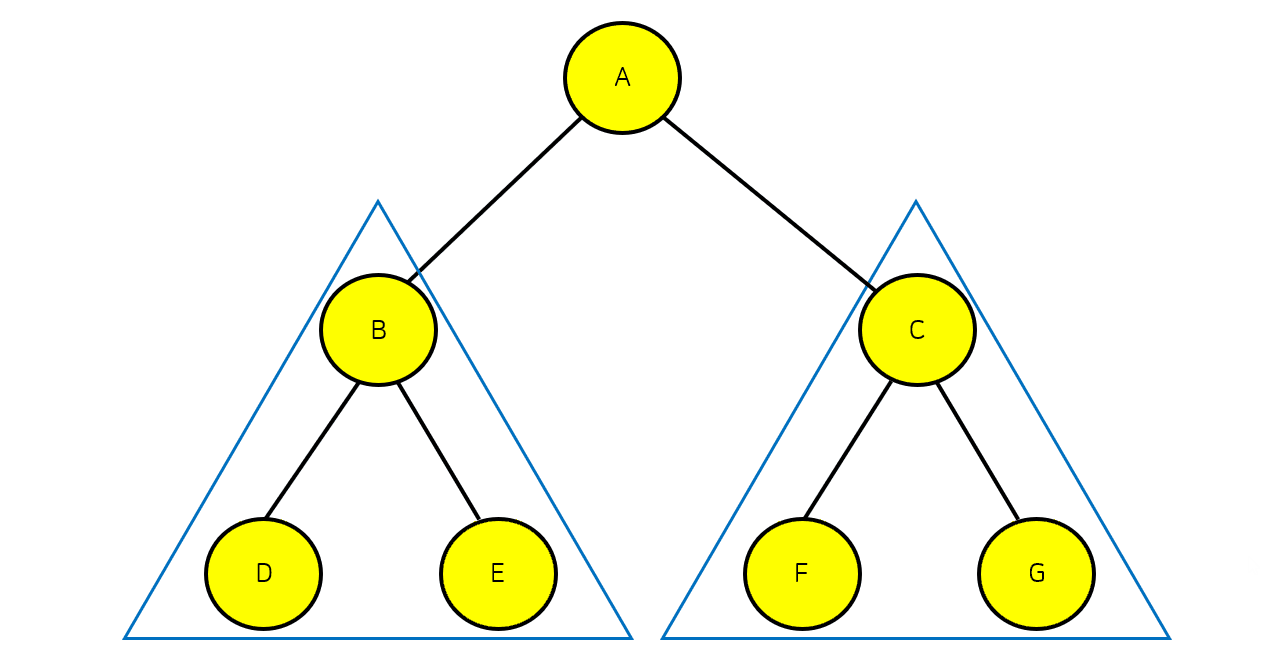
전위 순회는 루트를 먼저 방문하는 순회 방법으로 루트노드 → 왼쪽노드 → 오른쪽노드 순으로 방문을 해준다. 서브 트리가 있는 경우 루트노드에서 왼쪽 서브트리로 이동 후 왼쪽 서브트리에 있는 노드들을 모두 방문했을 경우 오른쪽 서브트리에 있는 노드들을 방문해준다.

위의 트리의 전위 순회의 경우 A→B→D→E→C→F→G 이다.

# node 구현
class node:
  def __init__(self, value):
    self.value = value
    self.left = None
    self.right = None

# 트리 구현
root_node = node('A')
root_node.left = node('B')
root_node.right = node('C')
root_node.left.left = node('D')
root_node.left.right = node('E')
root_node.right.left = node('F')
root_node.right.right = node('G')

# 전위순회 구현
def preorder(node):
  if node:
    print(node.value) # root node
    preorder(node.left)
    preorder(node.right)
  
  # root node → left node → right node 순으로 출력됨

중위순회 (inorder travers)

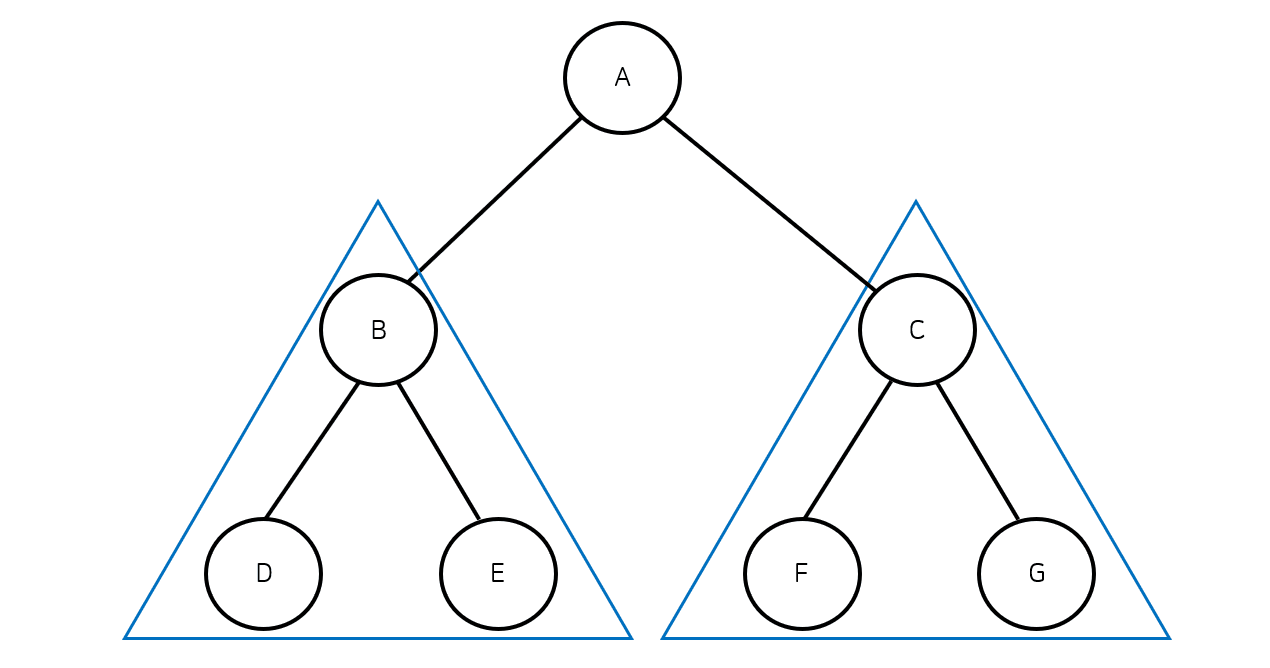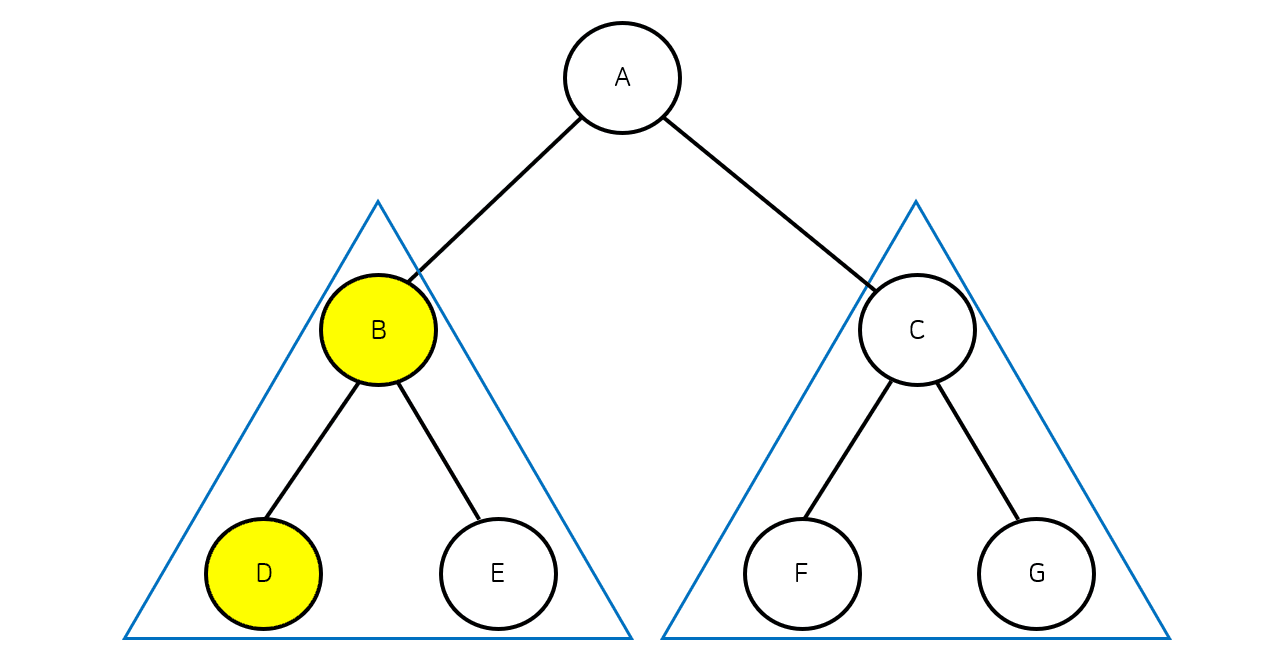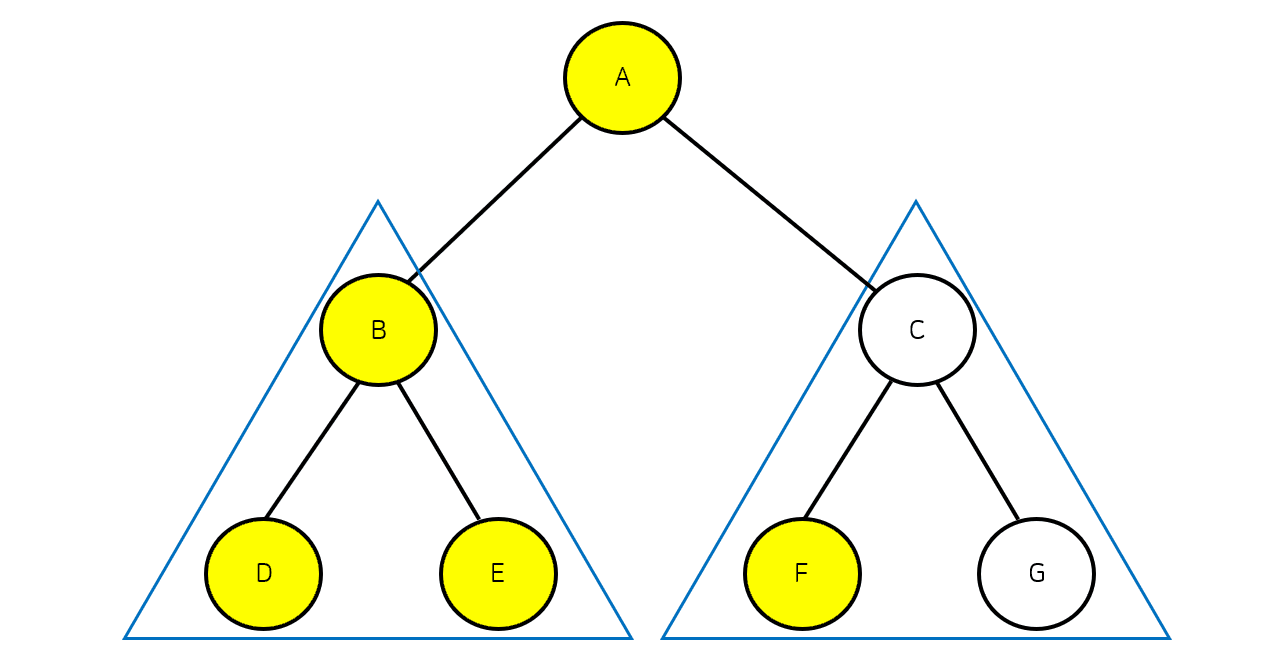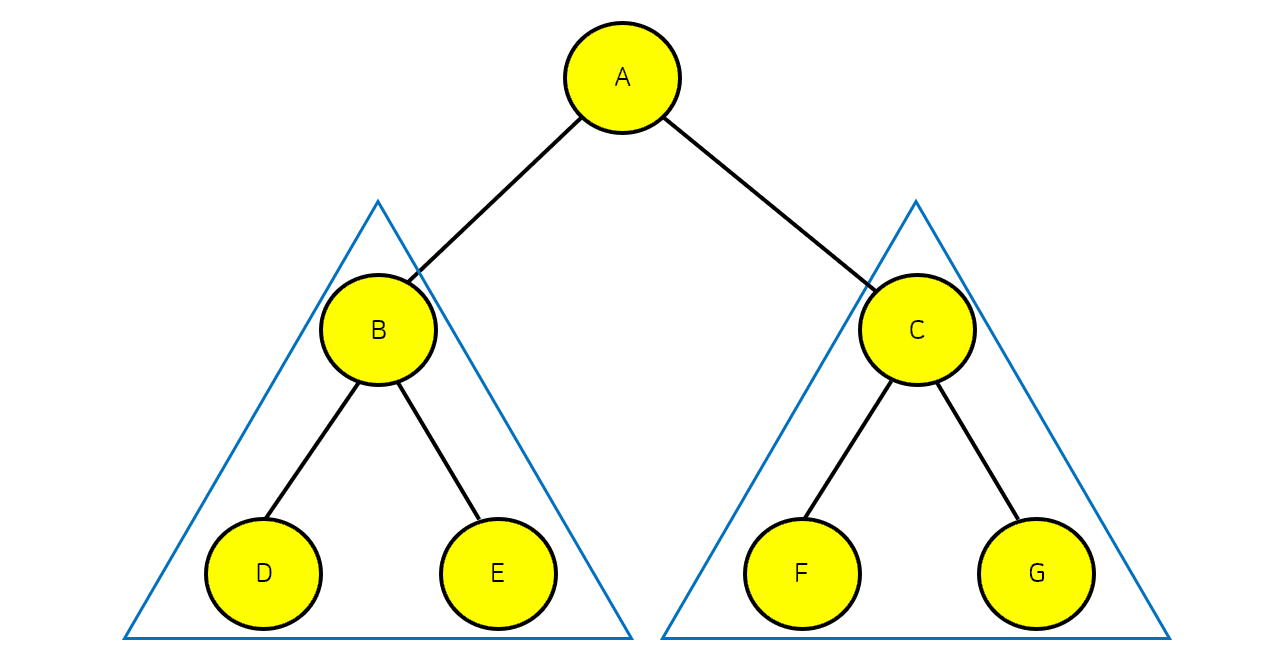
중위순회는 왼쪽 노드를 먼저 방문하는 순회 방법으로 왼쪽노드 → 루트노드 → 오른쪽노드 순으로 방문을 해준다. 전위순회에서 설명했듯이 서브트리가 있는 경우도 똑같이 진행해주면 된다.

위의 트리의 중위순회 결과는 D→B→E→A→F→C→G 이다.

def inorder(node):
  if node:
    inorder(node.left)
    print(node.value)
    inorder(node.right)
  
  # left node → root node → right node 순으로 출력됨

후위순회 (postorder travers)

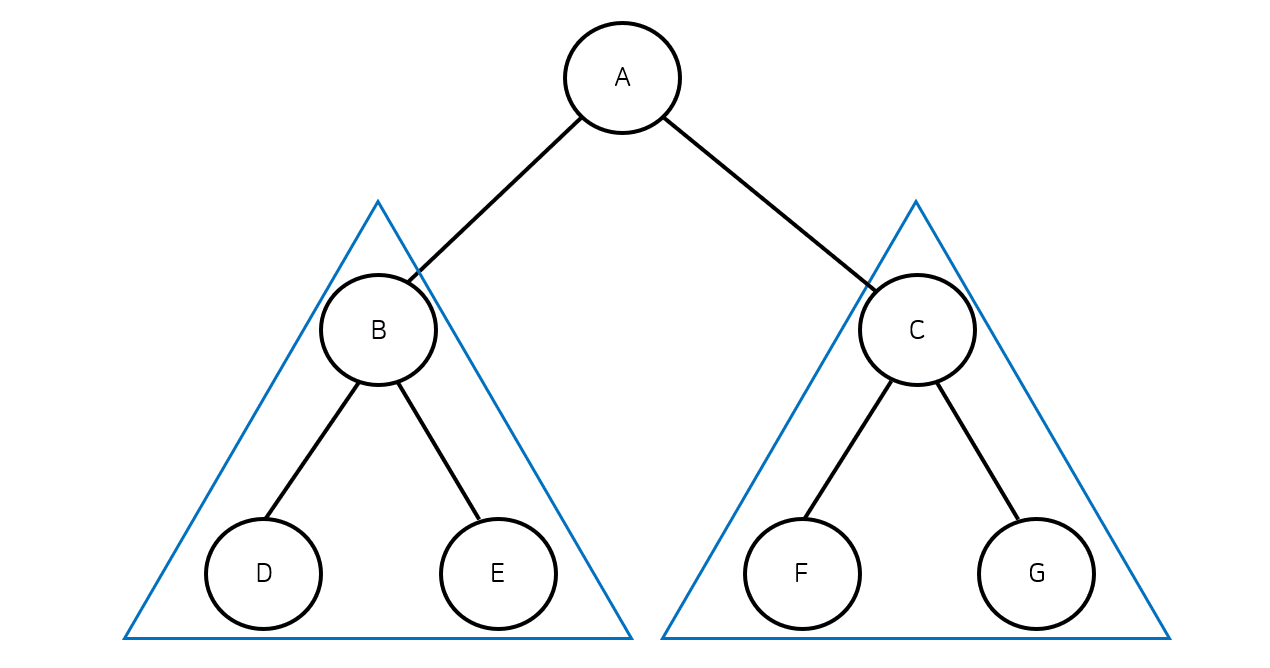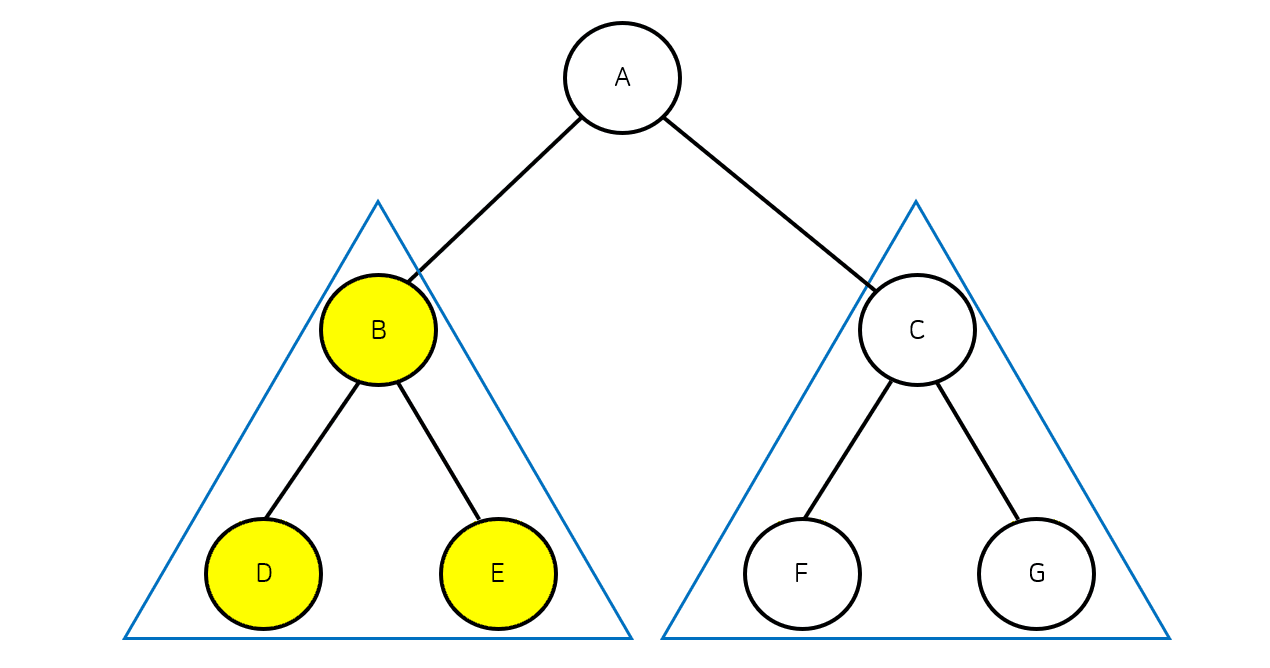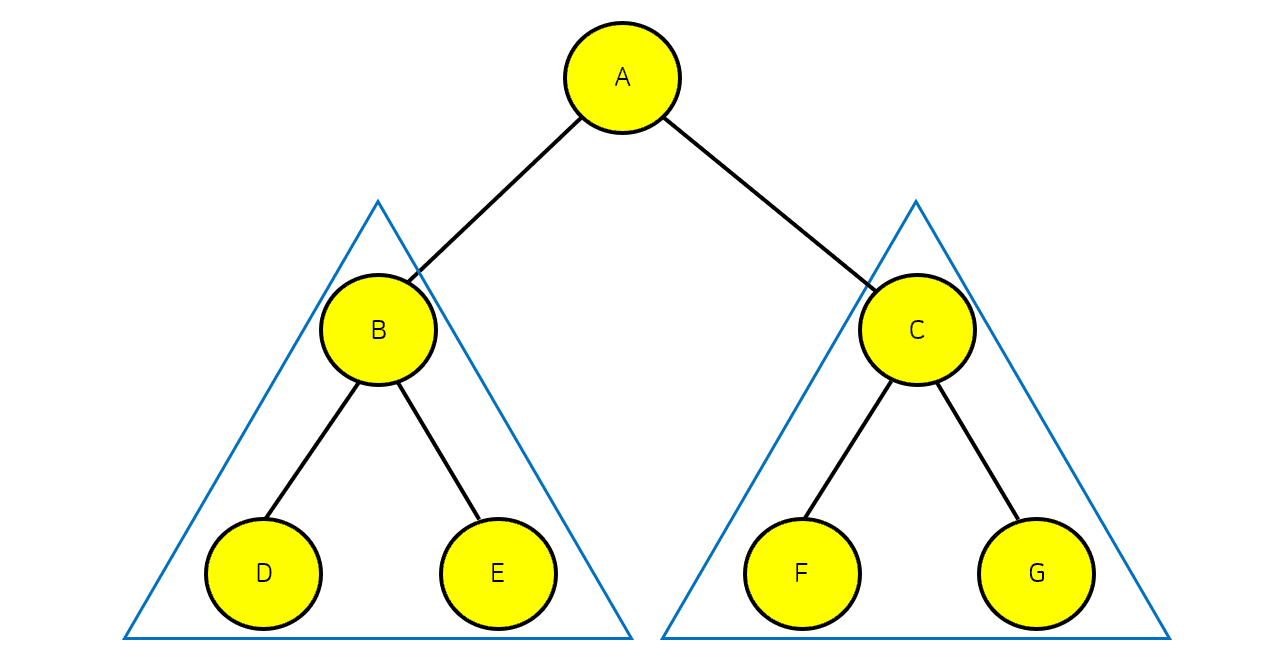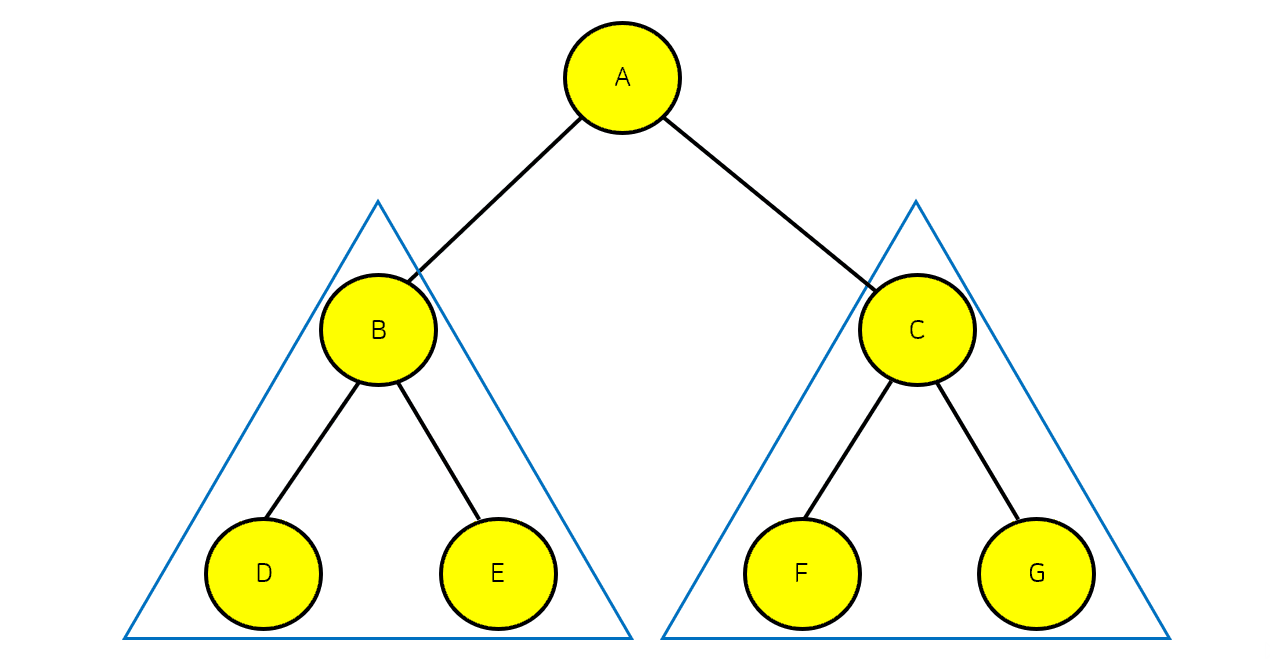
후위순회는 중위순회와 마찬가지로 왼쪽노드를 방문하지만 그 뒤 루트노드가 아닌 오른쪽노드를 방문하는 순회방법으로 왼쪽노드 → 오른쪽노드 → 루트노드 순으로 방문하는 방법이다.

위의 트리의 후위순회 결과는 D→E→B→F→G→C→A이다.

def postorder(node):
  if node:
    postorder(node.left)
    postorder(node.right)
    print(node.value)
  
  # left node → right node → root node 순으로 출력됨

DFS (Depth First Traversal)

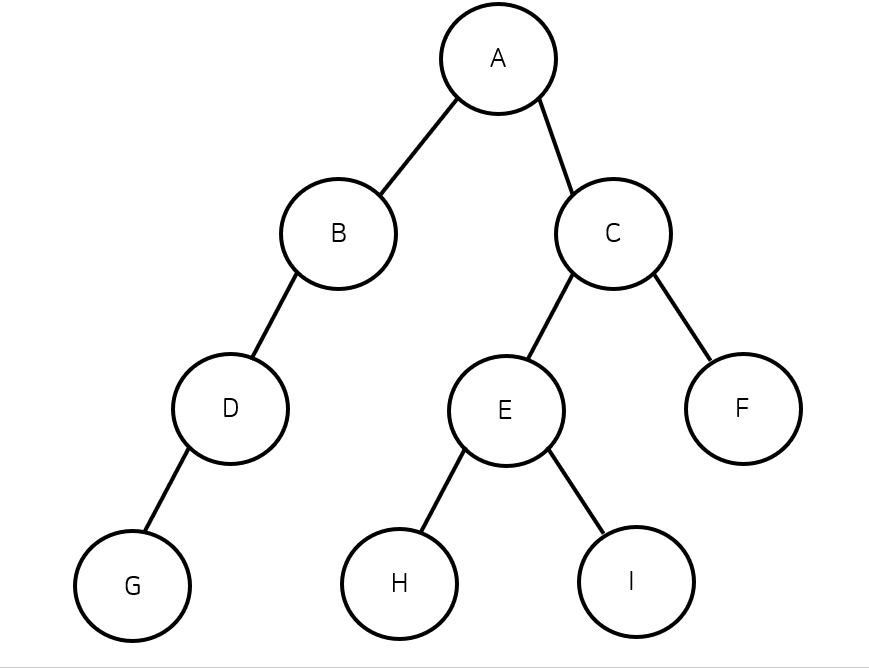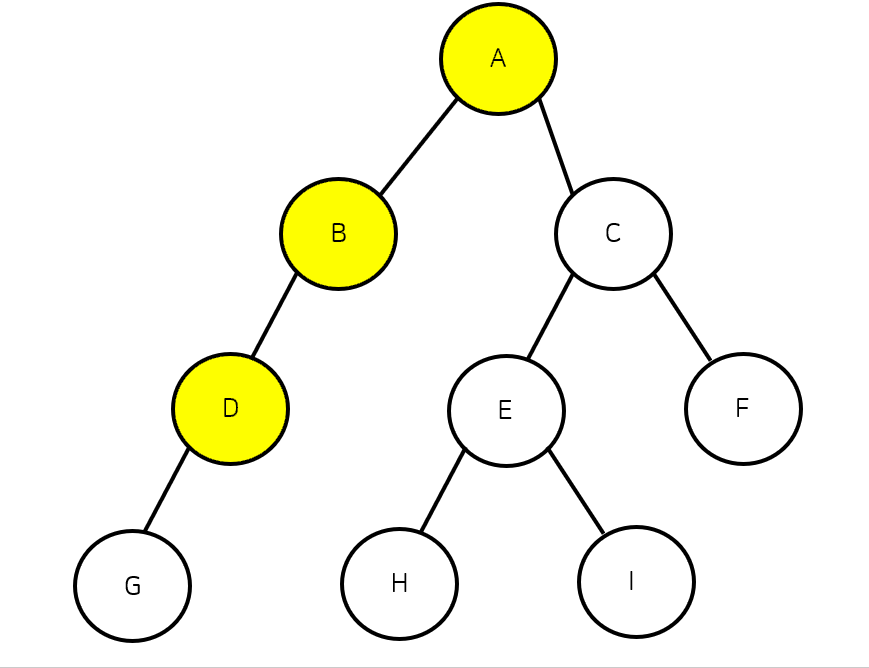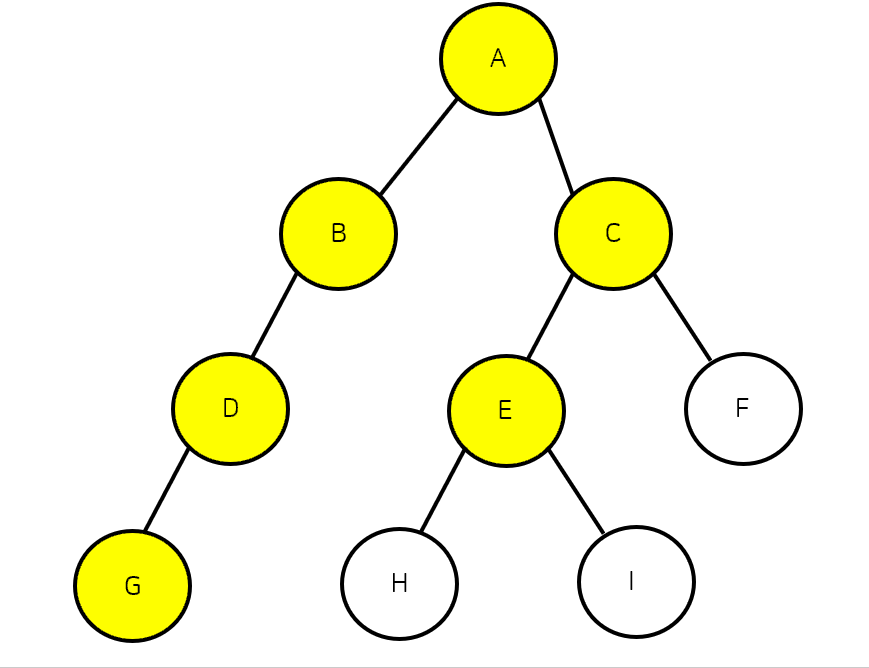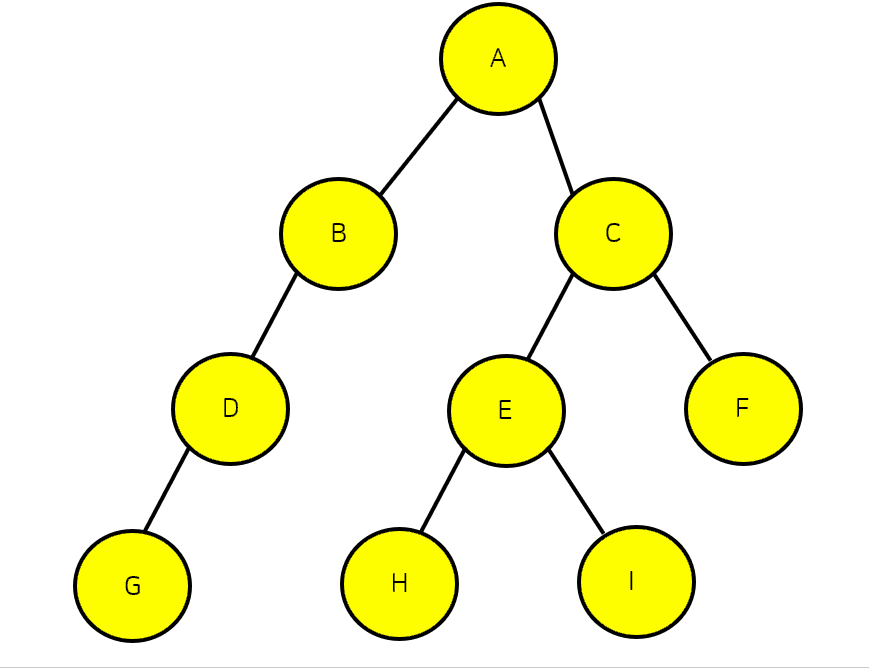
DFS는 탐색 알고리즘 중 하나로 깊이 우선 탐색이라고도 부른다. DFS는 현재 노드에서 갈 수 있는 노드까지 깊게 들어가면서 탐색을 하는 알고리즘으로 재귀함수 혹은 스택으로 구현이 가능하다. 만약 탐색 중에 동일한 깊이의 인접노드가 여러개 있다면 이 중 노드의 값이 작은 것부터 차례대로 탐색하게 된다.

graph = [
  [],
  [2, 3, 8],
  [1, 7],
  [1, 4, 5],
  [3, 5],
  [3, 4],
  [7],
  [2, 6, 8],
  [1, 7]
]

def dfs_stack(graph, start_node):
  stack, visited = list(), list()
  
  stack.append(start_node)
  
  while stack:
    node = stack.pop()
    # 만약 현재 노드가 방문 목록에 없으면 방문 목록에 추가
    if node not in visited:
      visited.append(node)
      # 현재 노드와 연결된 노드를 방문 목록에 추가
      stack.extend(graph[node])
  
  return visited

def dfs_recur(graph, v, visited):
  # 현재 노드를 방문 처리
  visited[v] = True
  print(v + ' ')
  
  # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
  for i in graph[v]:
    if not visited[i]:
      dfs(graph, i, visited)

BFS (Breadth First Traversal)

BFS는 DFS와 마찬가지로 탐색 알고리즘 중 하나이다. 너비 우선 탐색이라고도 불리며 현재 노드에서 연결된 가까운 노드부터 탐색 하는 알고리즘이다. BFS도 동일한 깊이의 노드가 여러개 있다면 노드의 값이 작은 노드부터 탐색한다.

from collections import deque

def bfs(graph, start, visited):
  queue = deque([start])
  
  visited[start] = True
  
  while queue:
    v = queue.popleft()
    print(v + ' ')
    for i in graph[v]:
      if not visited[i]:
        queue.append(i)
        visited[i] = True