그래프 (Graph)

그래프는 정점(노드라고도 함, vert)과 간선(edge)으로 이루어진 자료구조로 트리와 연관된 개념이다. 트리와 그래프의 차이는 아래 사진과 같다.

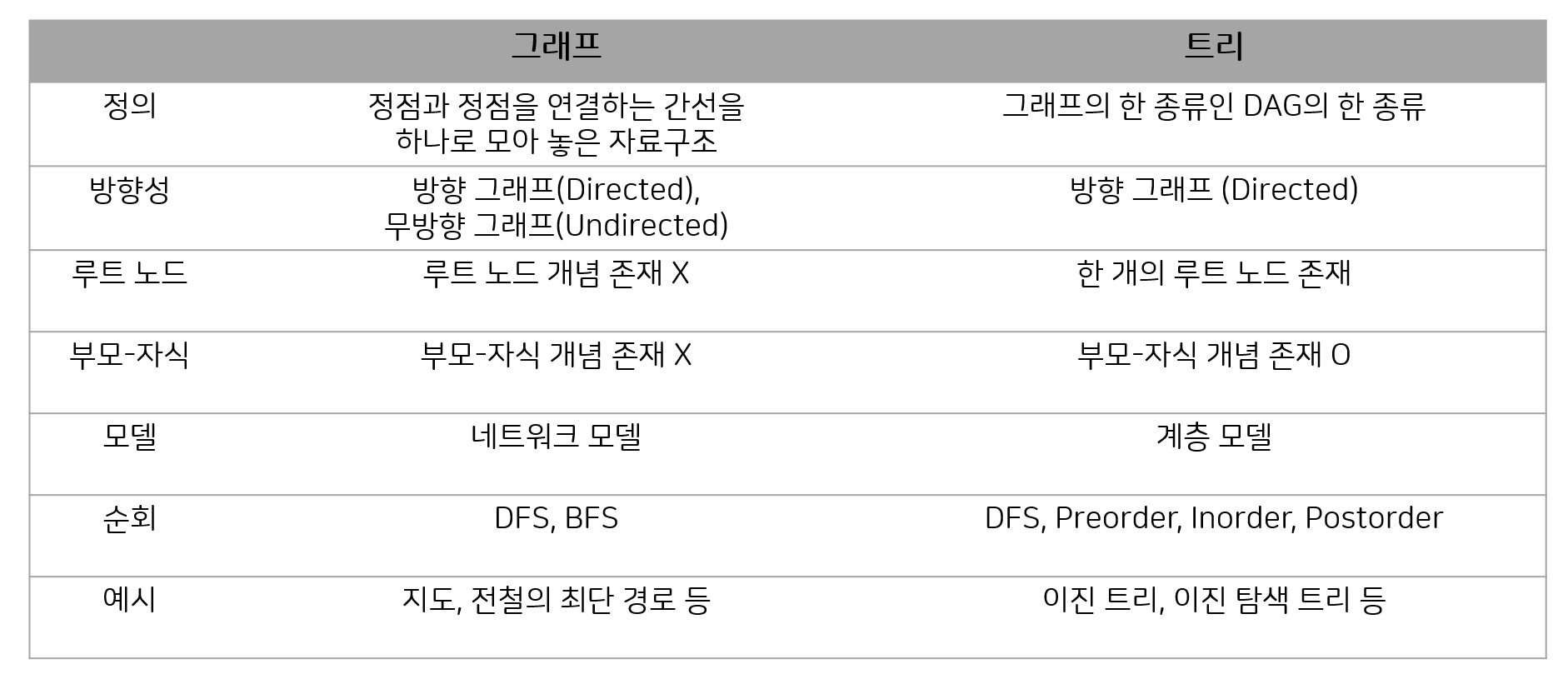
종류

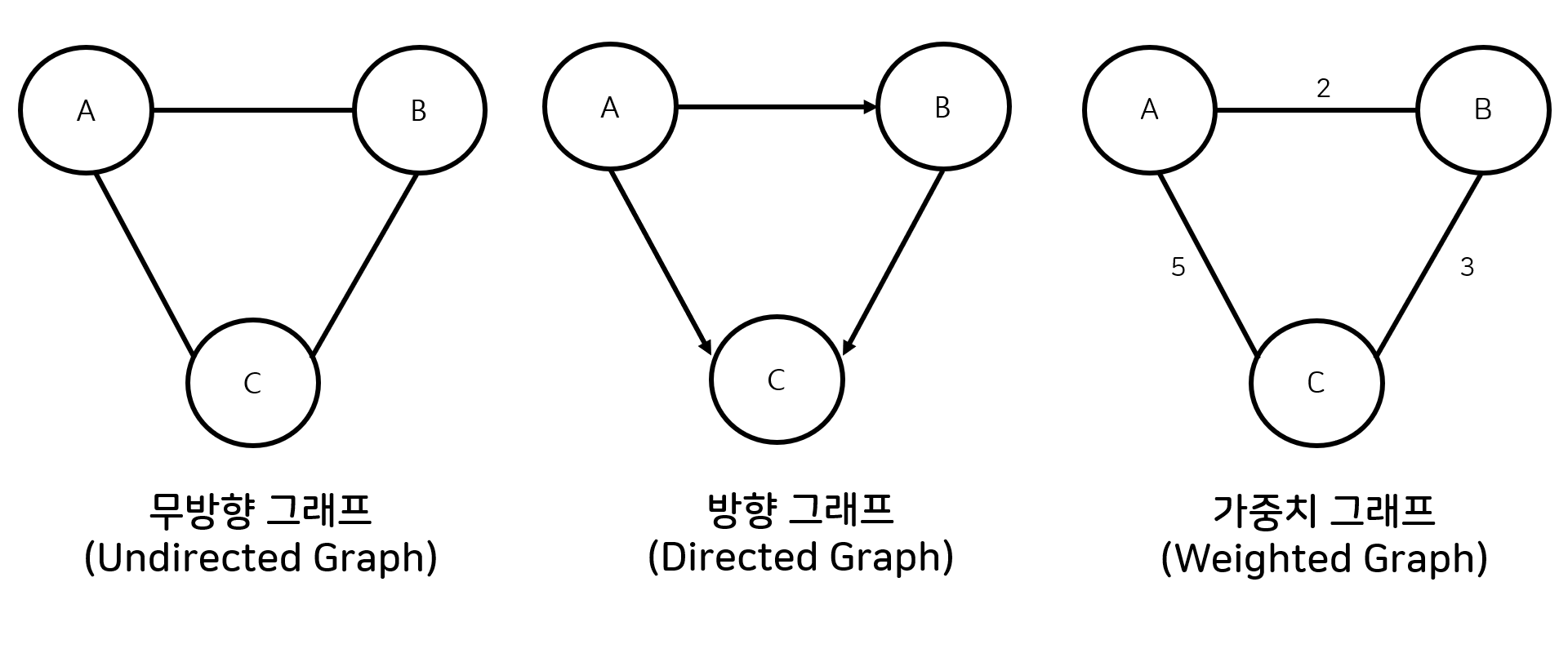
• 무방향 그래프: 두 노드를 연결하는 간선에 방향이 없는 그래프
• 방향 그래프: 두 노드를 연결하는 간선에 방향이 있는 그래프. 간선의 방향으로만 이동할 수 있음
• 가중치 그래프: 간선에 가중치가 할당된 그래프. 두 노드를 이동할 때 비용이 드는 그래프

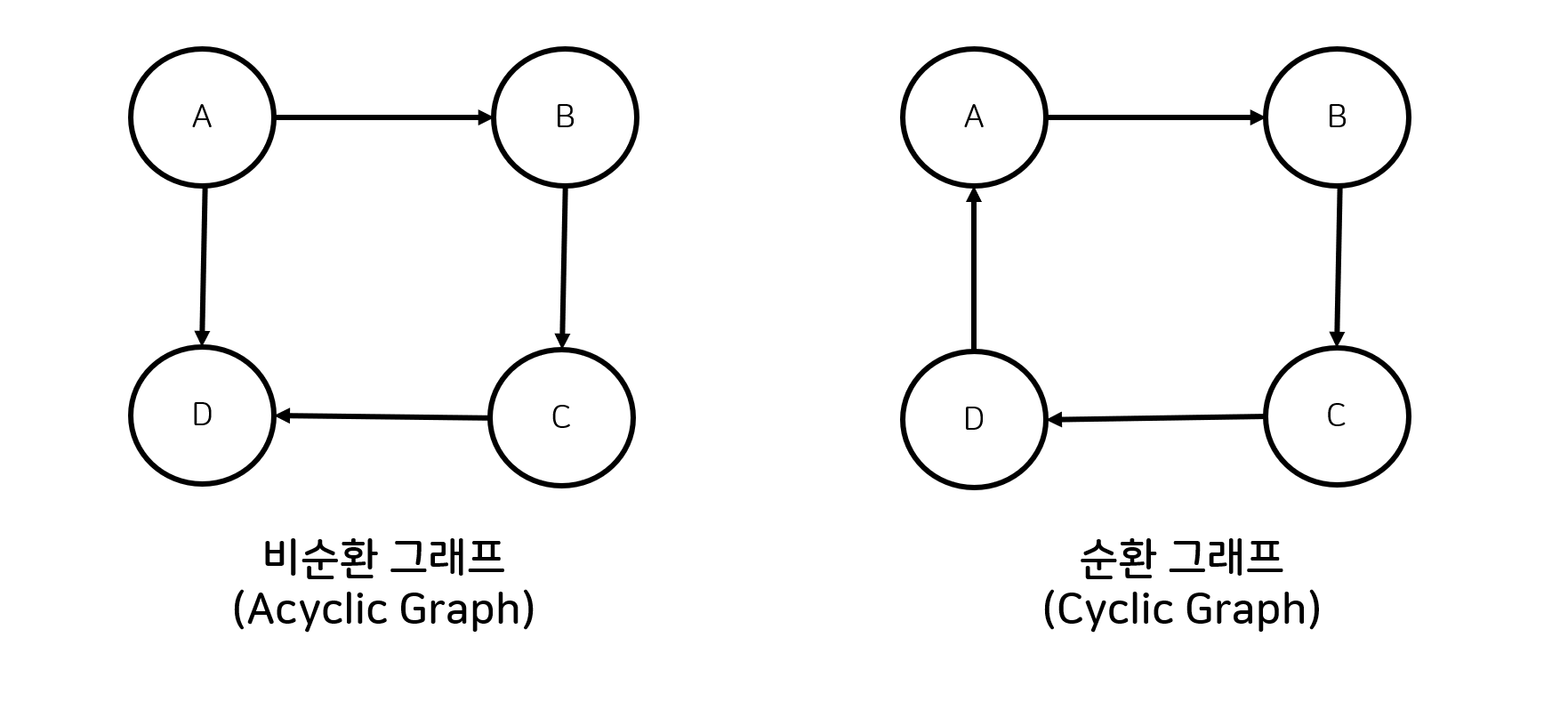
• 비순환 그래프: 순환이 없는 그래프
• 순환 그래프: 시작 노드와 도착 노드가 동일한 그래프. (A에서 시작 -> A에서 끝)

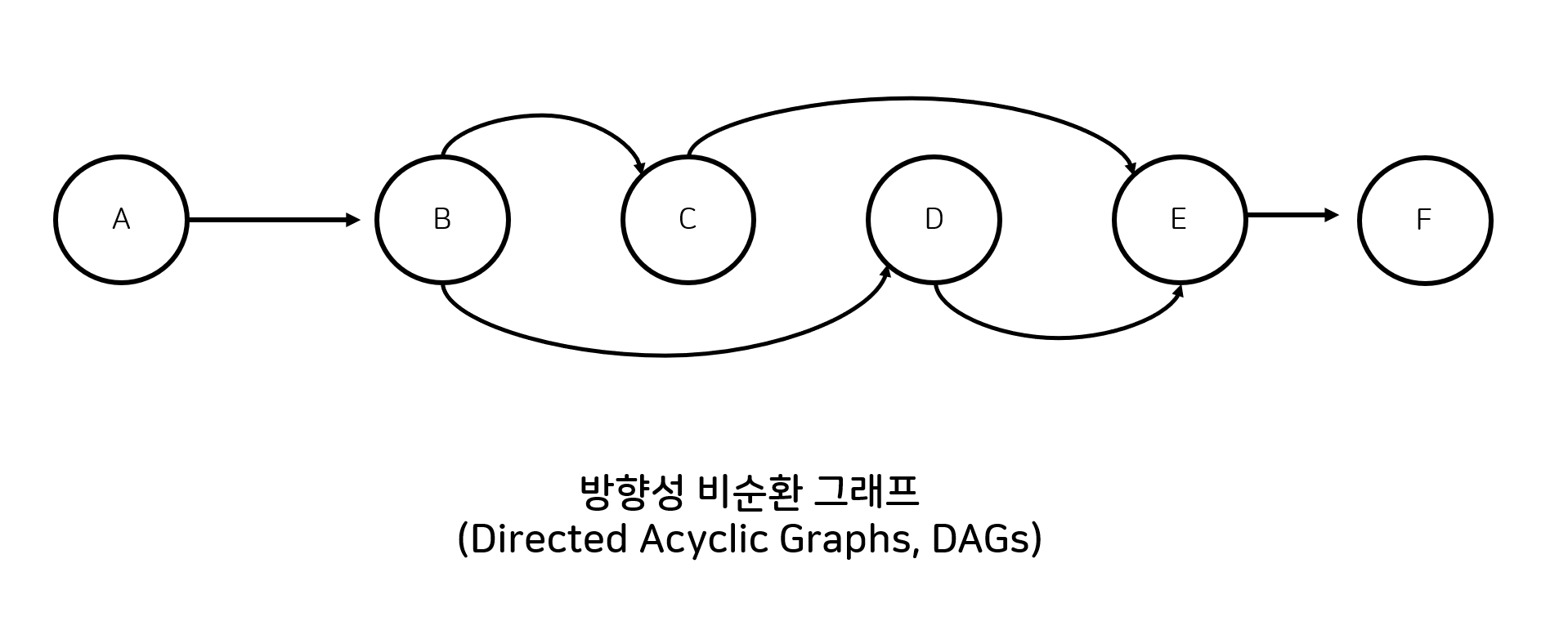
• 방향성 비순환 그래프: 개별 노드들이 특정 방향을 향하고 순환하지 않는 그래프

인접 리스트 (Adjacency List)

인접 리스트 그래프는 전체 노드 목록을 저장한다. 노드가 키가 되고 인접 노드가 값이 되는 딕셔너리로 구현한다.

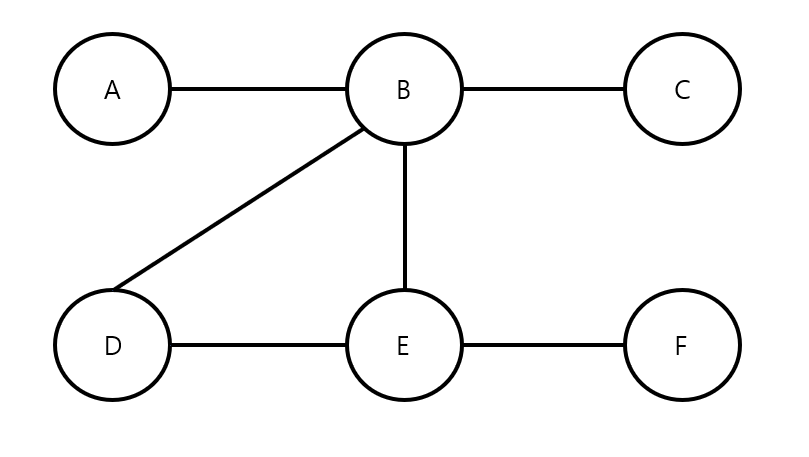
위의 그래프를 인접 리스트로 표현하면 아래와 같다.

adjacency_list = {
  'A': {'B'},
  'B': {'C', 'D', 'E'},
  'C': {'B'},
  'D': {'B', 'E'},
  'E': {'B', 'D', 'F'},
  'F': {'E'}
}

인접 행렬 (Adjacency Matrix)

인접 행렬은 노드간 연결이 되어 있으면 1, 연결이 되어있지 않으면 0으로 표현한 행렬로 2차원 배열로 구현할 수 있다. 만약 가중치 행렬이라면 1이 아닌 가중치 값을 넣어서 표현할 수 있다.

위의 그래프를 인접 행렬로 표현하면 아래와 같다.

adjacency_matrix = [
  [0, 1, 0, 0, 0, 0],
  [0, 0, 1, 1, 1, 0],
  [0, 1, 0, 0, 0, 0],
  [0, 1, 0, 0, 1, 0],
  [0, 1, 0, 1, 0, 1],
  [0, 0, 0, 0, 1, 0]
]