오늘은 어제 배운 T-test를 이어서 배웠다.
T-test를 사용하기 위한 조건
독립성
독립성은 두 그룹이 연결되어 있는 (paired) 쌍인지를 확인한다. 만약 서로 짝지어진 자료라면 대응표본 T 검정을 실시한다.
정규성
정규성은 데이터가 정규성을 나타내는지를 확인한다. 만약 정규분포가 아니라면 Mann-Whitney test를 실시한다.
등분산성
등분산성은 두 그룹이 어느정도 유사한 수준의 분산 값을 가지는지 확인한다. 두 그룹의 분산이 서로 다르다면 자유도를 수정한 독립표본 T 검정을 실시한다.
Type of Error
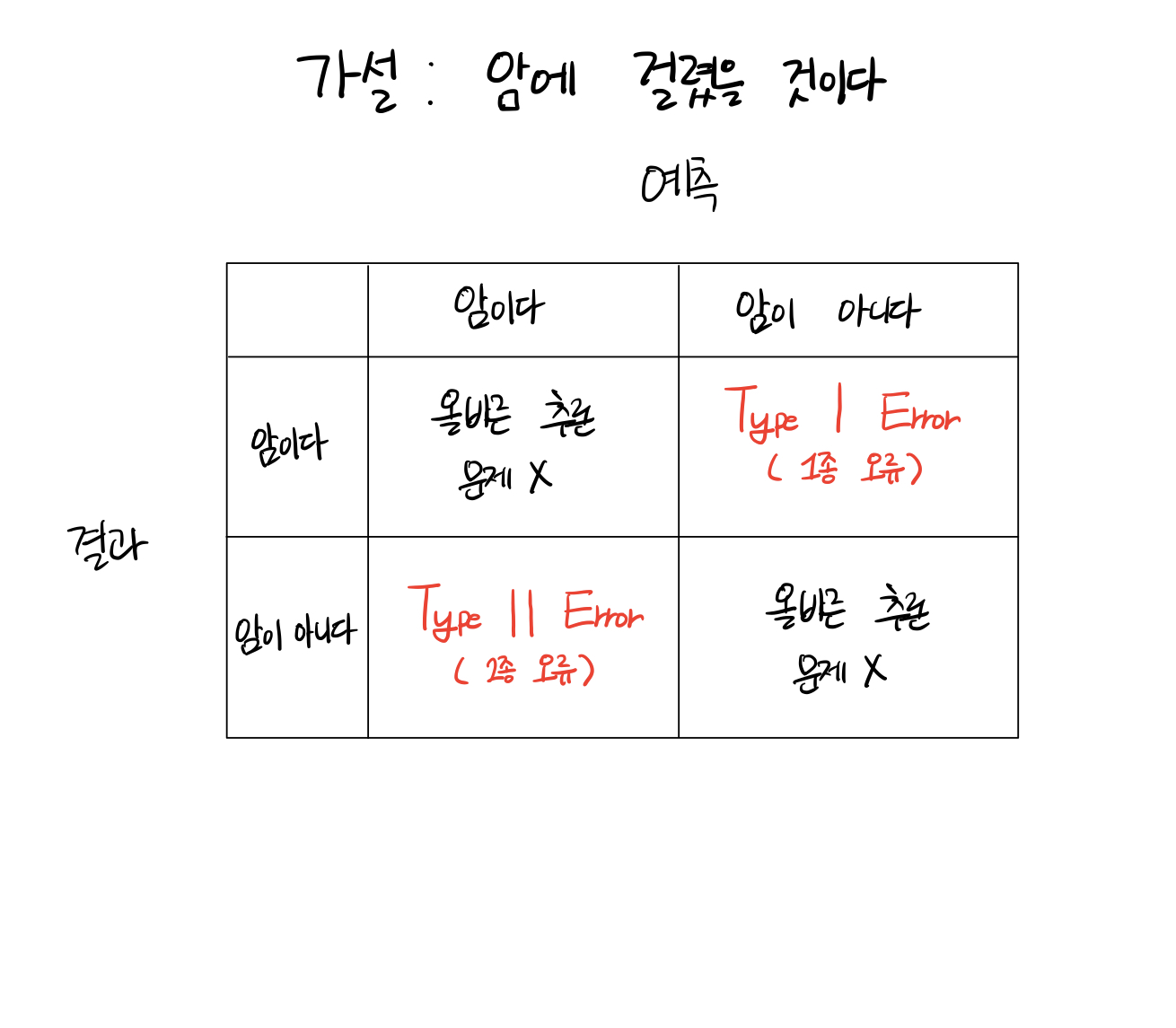
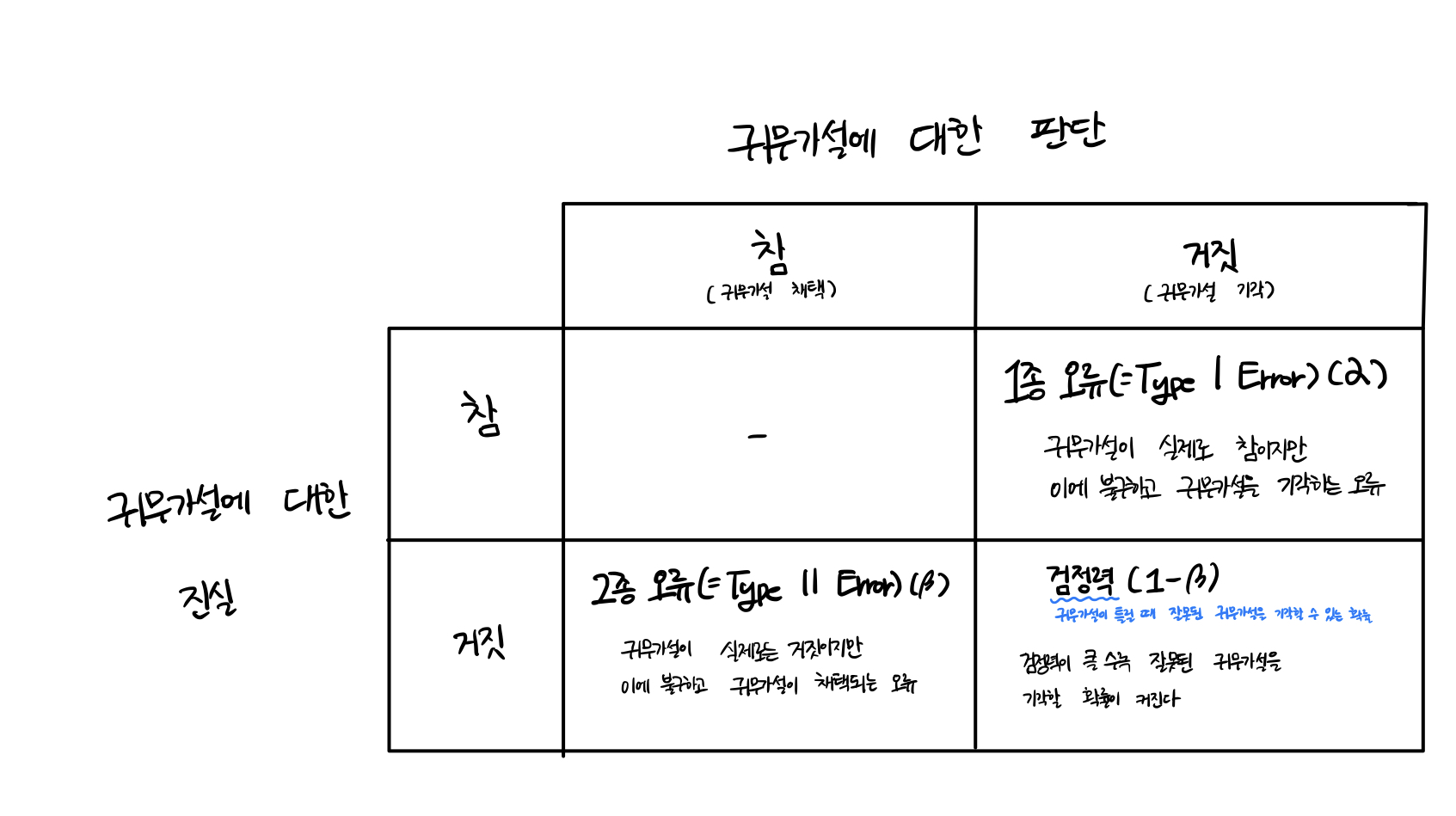
1종 오류는 귀무가설은 사실인데 가설 검정을 틀렸다고 하는 경우이고, 2종 오류는 귀무가설이 틀렸는데 가설 검정은 사실이라고 하는 경우이다.
이를 아래의 표와 같이 한번 정리해봤다.
Non-Parametric Methods
비모수적 방법 (Non-Parametric Method)는 모집단이 특정 확률 분포를 따른다는 전제를 하지 않는 방식이다. 기억하기로는 수가 적은 경우도 포함된다고 한다. 예를 들면 모집단이 서른명밖에 안된다거나 하는 경우이다.
비모수적 방법은 distribution free method라고 부르기도 한다. 극단적인 outlier가 있는 경우에 매우 유효한 방식이다.
비모수적 방법에는 Chisquare, Spearman correlation, Run test, Mann-Whitney U 등 다양한 방식이 있다.
카이제곱 검정 (chi-square)
카이제곱 검정은 데이터 분포, 빈포, 비율에 대해서 검정하는 방법이다. 주어진 데이터가 특정 예상되는 분포와 동일한 분포를 나타내는지에 대해 가설검정을 한다. Goodness of Fit test라고 부르기도 한다.
카이제곱 검정에서 귀무가설은 분포가 비슷하다고 설정하고, 대립가설은 분포가 비슷하지 않다고 설정한다.
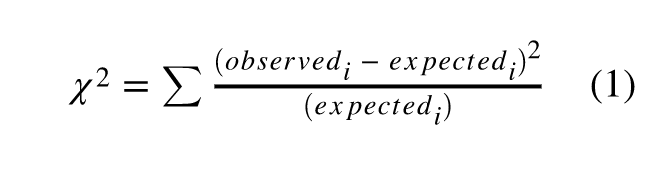
위의 수식은 카이제곱의 통계량을 계산하는 수식이다. 여기서 observed는 관찰빈도 즉 관측값이고 expected는 기대빈도 즉 예상값이다.
위의 수식에서 제곱을 해 주는 이유는 관측값에서 예상값을 뺀 결과가 음수일 수도 있기 때문이다. 때문에 제곱시킴으로써 차이를 더 깊게 살펴볼 수 있다.
카이제곱 검정은 scipy의 chisquare 함수를 이용하면 쉽게 구할 수 있다.
from scipy.stats import chisquare
from scipy.stats import chi2_contingency
chisquare(data, axis=None) #one sample test
chi2_contingency(data, correction = True) #two sample testone sampel test를 위해 사용하는 chisquare 함수는 두가지 값을 리턴해준다. 첫번째로 statistic, 두번째는 pvalue값이다.
statistic 값은 stats.chi2.cdf 함수를 사용하면 pvalue 값으로 바꿀 수 있다고는 하는데 아직 해보지는 않았다...😅 추석 연휴에 시간이 많으니 그때 한번 돌려보고 더 공부한 내용이 있다면 추가해놔야지..
two sample test를 위해서 사용하는 chi2_contingency 함수는 4가지 값을 반환해준다. 두번째 인자까지는 chisquare 함수와 같고 세번째는 자유도(degree of freedom), 4번째는 기대값을 array 형식으로 반환해준다.
자유도 (degree of freedom)
자유도(d.f. = degree of freedom)는 주어진 조건에서 통계적 제한을 받지 않고 자유롭게 변화될 수 있는 요소를 말한다. 즉, 독립적으로 정해질 수 있는 값의 수를 말한다. 자유도는 정보의 손실 정도라고 할 수도 있고 독립변수의 개수라고도 부른다.
예를 들어서 x1, x2, x3의 세 값이 있고 세 값의 합은 10이라고 가정해봤다. 이때 x1의 값은 5, x2의 값은 3이라고 한다면 x3의 값은 2가 된다. 여기서 x1과 x2는 독립변수라고 하고 x3는 종속 변수가 된다.
자유도는 보통 df = n - 1이 된다. 위의 예제처럼 3개의 변수가 있다면 그 중 2개의 변수가 독립변수가 되는 것이다.


