재귀함수

재귀함수는 함수 안에서 그 함수를 다시 호출하는 것을 반복하는 함수 즉, 스스로를 반복적으로 호출하는 함수이다. 재귀함수를 반복적으로 호출할 때는 반드시 재귀호출 없이 해결할 수 있는 base case를 결정해야한다. 최소문제를 결정하지 않으면 무한 루프에 빠지게 되니 조심해야한다.

# 1부터 입력된 값까지의 합을 구하는 재귀함수
def recursive_call(num):
	if num < 1:
    	return num
    else:
    	return num + recursive_call(num-1)

재귀함수를 반복적으로 호출하게 되면 메모리를 더 많이 사용하게 되기 때문에 재귀함수는 되도록이면 사용하지 않는게 좋다. 다만 수학적으로 개념이 복잡한 경우에는 메모리 사용 효율이 좋지 않더라도 재귀를 사용해서 문제를 해결하는 것이 좋다고 한다.

트리 (Tree)

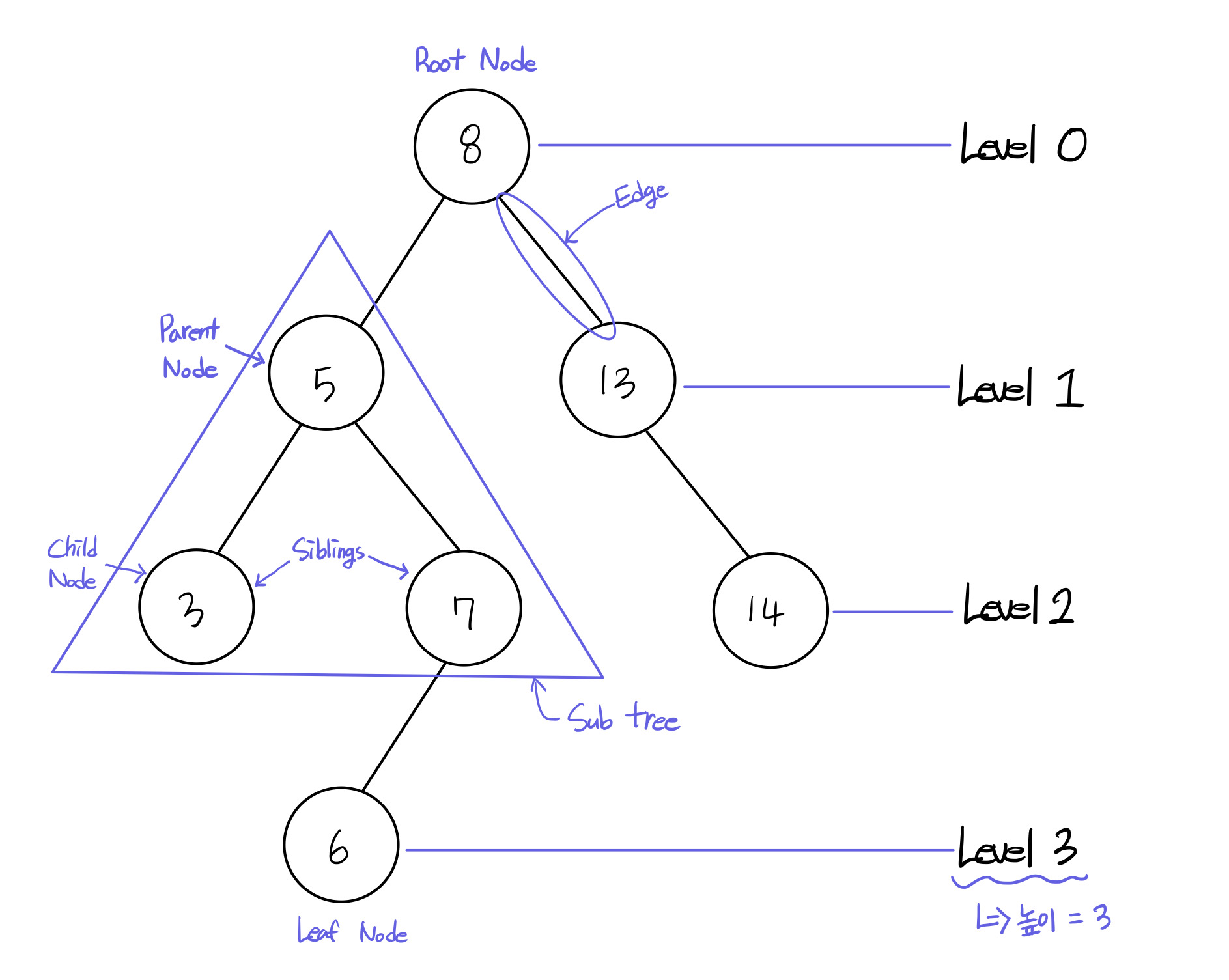
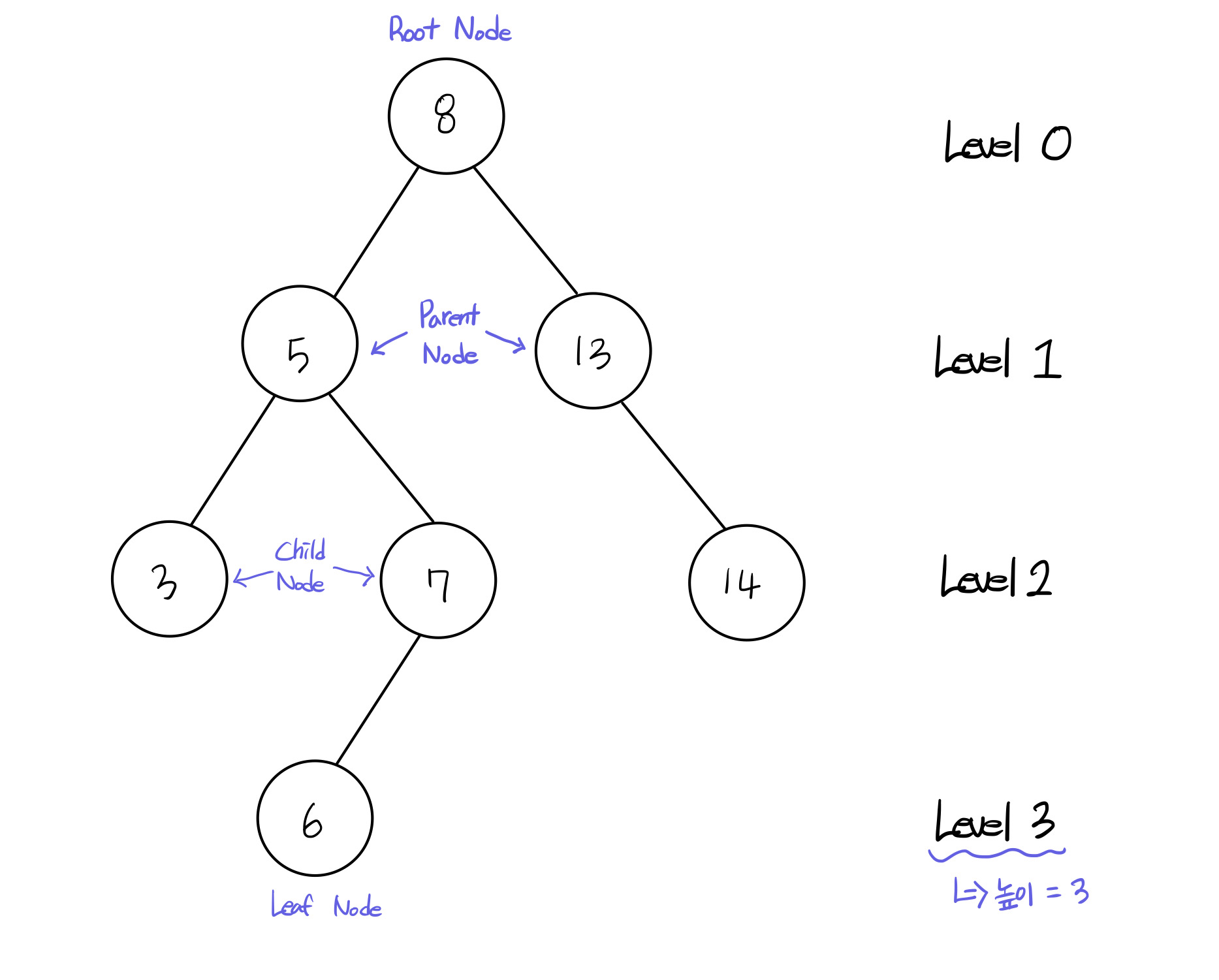
트리는 노드들이 나뭇가지처럼 연결된 비선형 계층적 자료구조이다. 또한 트리 내에 다른 하위 트리가 있고 그 하위 트리 안에는 또 다른 하위 트리가 있는 재귀적 자료구조이기도 하다.

용어

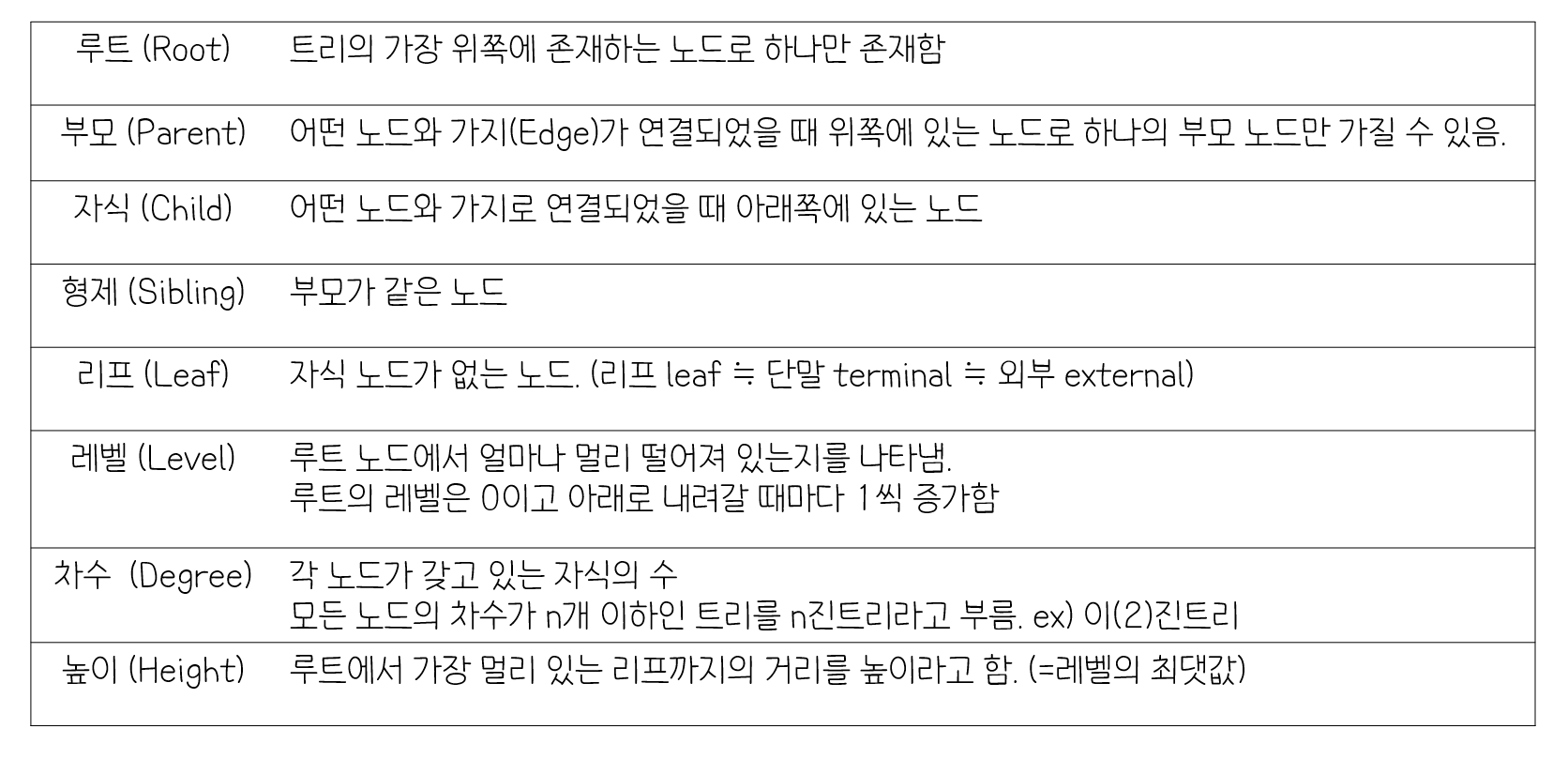
이진 검색 트리 (BST, Binary Search Tree)

트리 중에 자식 노드가 최대 2개가 붙는 트리를 이진 트리 혹은 바이너리 트리라고 부른다. 그 중 이진 탐색 트리(BST)는 노드를 정확하게 정렬해야하는 특정 유형의 이진 트리이다. BST는 단순한 이진 트리보다 빠르게 노드를 탐색하기 위해서 값 크기 조건에 맞도록 값을 넣어주는 경우가 이진 탐색 트리이다.

값 크기의 조건은 오른쪽 서브 노드(right child)의 값 > 루트 노드(root node or parent node)의 값 > 왼쪽 서브노드(left child)의 값이다. 또한 중복 값을 갖고 있는 노드가 없어야 한다.

값 크기 조건이 정해진 이유는 BST가 왼쪽부터 오른쪽으로 검색을 하는 구조이기 때문이다. 이와 같은 조건에 따라 구조가 단순하고 검색이 단순 이진트리보다 빠르기 때문에 노드를 삽입하기 쉽다는 특징을 갖고 있다.

# 이진 검색 트리 구현

class Node:
  def __init__(self,value):
    self.value = value
    self.right = None
    self.left = None

class bst:
  def __init__(self, head):
    self.head = head
  
  def insert_node(self, value):
    self.base_node = self.head

    while True:
      if value < self.base_node.value:
        if self.base_node.left != None:
          self.base_node = self.base_node.left
        else:
          self.base_node.left = Node(value)
          break
      else:
        if self.base_node.right != None:
          self.base_node = self.base_node.right
        else:
          self.base_node.right = Node(value)
          break
  
  def search_node(self, value):
    self.base_node = self.head

    while self.base_node:
      # base node와 찾으려는 값이 일치하면 탐색을 종료함
      if self.base_node.value == value:
        return True
      # 만약 찾으려는 값보다 base node의 값이 크면 왼쪽으로 이동해 탐색함
      elif self.base_node.value > value:
        self.base_node = self.base_node.left
      # 만약 찾으려는 값보다 base node의 값이 크면 오른쪽으로 이동해 탐색함
      elif self.base_node.value < value:
        self.base_node = self.base_node.right
    
    return False